Physics - Electromagnetism - Electric resistance
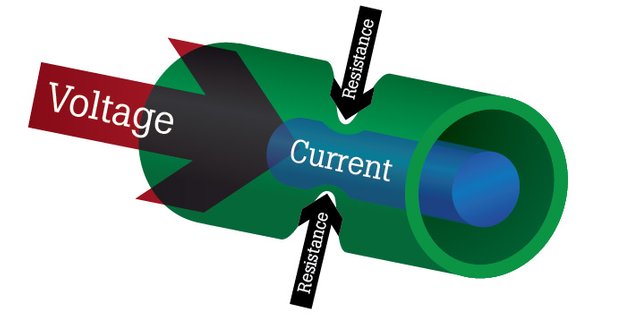
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into Electric resistance!
This post might seem similar to the previous post, but it actually isn't exactly the same topic. But you could think about it as some kind of part2 :P
All the mathematical equations will be drawn using quicklatex!
So, without further do, let's get straight into it!
Resistance definition
Last time we covered that a conductor that obeys Ohm's law (ohmic conductor) has a special resistance or electric resistivity ρ that is given by:
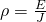
where:
- ρ is the electric resistivity of a conductor
- J the electric current density at some point
- E the electric field that acts inside of the conductor
Of course ρ is a constant number (when having an ohmic conductor) and this means that J is also proportional to E which can be noted as:
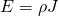
But these equations of course contain only the electric field E and electric current density J and not the electric current I and potential difference V, which we care about much more!
Let's condiser a wire conductor with constant cross-section area A and length L.
The electric current density J and electric field E have the same magnitude for all the points inside of the conductor, which means that the current and potential difference (or voltage) are given by:
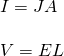
You might remember the first one better as:
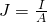
For the second one think about the equation:
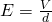
by changing d->L we of course get the equation.
By placing each one in the first equation we get the voltage:
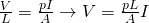
An equation that tells us that the voltage and electric current are proportional to each other if ρ is constant and cause L and A are wire properties.
The ratio V/I for a specific conductor is called resistance R:
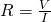
By replacing the voltage with the previously proven equation we get:
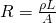
which shows us that the resistance is constant if ρ is constant and that the resistance is proportional to the length L and resistivity ρ, and inverse proportional to the area A.
Note that the equation:
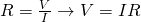
gives us the resistance for any conductor, and so even if it doesn't obey Ohm's law, but this formula is called Ohm's law only when talking about an ohmic conductor that has a constant resistance R (which means that ρ is constant).
The SI unit of resistance is the ohm (Ω) which is:
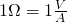 (volt/ampere)
(volt/ampere)
but we again will talk about kΩ, MΩ etc. in our examples.
Resistance and temperature
Because the electric resistivity ρ changes value when the temperature changes, the resistance R also depends temperature.
For a small range of temperatures we can desribe this dependence using the linear equation (which is the "same" that we had with electric resistivity ρ):
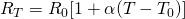
where:
- RT is the resistance at temperature T
- R0 is the resistance for a reference temperature T0
- α is the thermal coefficient of resistance, which has the same value that we had with ρ
The change of resistance is given by:
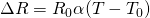
Resistor in electronic circuits
The electric circuit component with set resistance is called a Resistor.
Resistors mostly have:
- a cylinder shape
- diameter of some mm and
- wires (leads) that stick out on every end.

The actual resistance is described by the striped colors that the resistor has:
I actually have played around with resistors and led lights in a course where we covered Arduinos and FPGA's!
Also, note that resistors have a specific endurance/durability, which is the maximum voltage that they can consume without breaking apart.
In electronic circuit diagrams we note them like that:
The graph of voltage and current for ohmic conductors with constant temperature looks like this:
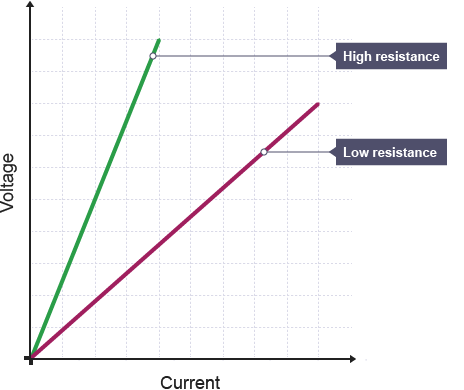
where the slope of this line is 1/R!
But, for other conductors we see more complex shapes which are:
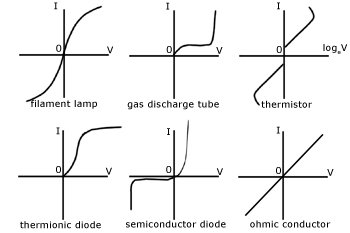
The relation of current-voltage depends a lot on the temperature. At smaller temperatures the curve increases mostly faster for positive voltages and the asymmetry of the curve becomes more and more clear.
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
And this is actually it for today!
Next time I will cover Electromotive Force!
Bye!
Hi, @drifter1.
If you have any problem regarding STEM-related articles, you can join steemSTEM Discord Channel and we will be glad to assist you.
Hey, thanks for pointing all these things out!
Greetings @drifter1.
Thank you for all these tips!!
I will keep all that in mind for my next posts!
Hi @drifter1!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
nice