Physics - Classical Mechanics - Position, velocity and acceleration vectors in a plane motion
Hello it's a me again drifter1! We have exams in a week and that's why I don't have so much time because I have to study, but here I am again to post about Physics again! Today we will get into 2-dimensional motion or plane motion and more specifically get into position, velocity and acceleration vectors in such a motion. So, without further do, let's get started!
Getting into 2 dimensions
In my previous posts we only talked about one dimension or one axis and movement that happens only on that specific axis. All the vectors where one-dimensional and that made them have only 2 possible directions that can be left/right or up/down depending on the problem, and they could also be zero.
But, using one axis and one dimension is not enough to describe the physics phenomena around us, and so we will have to get to 2 or even 3 dimensions, depending on the problem that we want to solve.
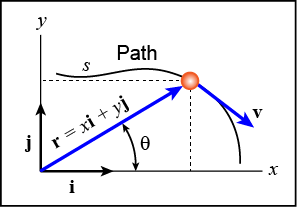
To get into 2 dimensions the position now needs to be a position vector, mostly called r, that has a value that represents the distance to the center O(0, 0, ..., 0).
So, the position now is:
r = xi + yj + zk + ... if we need even more dimensions
This can also be written as:
r = (x, y, z) in the classic format of a Point
Velocity vector
Using this new vector representation of position, but the same exacty logic we used in one dimension, we can now describe the velocity in 2 or even more dimensions.
The Change of position is Δr = r2 - r1.
Using it we can now specifiy the average velocity as:
u avg = Δr / Δt = r2 - r1 / t2 - t1
Because r1 and r2 are now vectors we can clearly see that the result of that equation is an vector that describes the velocity better as an vector and doesn't give us a numeric value as in 1D.
By calculating the limit when Δt -> 0 of Δr, Δr becomes a tangent of the line that describes the position in time, and so describes the direction of the instantaneous velocity and so equals the instantaneous velocity.
So, the instantaneous velocity is being calculated by:
u = lim Δt -> 0 (Δr/Δt) = dr/dt
To find the actual velocity value we can either calculate the meter of that vector u or can also find the velocity in each dimension separately.
The (instantaneous) velocity in each dimension is:
ux = dx/dt
uy = dy/dt
uz = dz/dt
etc...
Where ux, uy, uz, ... are the vector components of u
And this means that we can representate the velocity as:
u = dr/dt = dx/dt i + dy/dt j + dz/dt k + ...
using the unit vectors: i, j, k, ...
That way we can now also see that the actual velocity value and so the velocity vector meter is equal to:
|u|= root(ux^2 + uy^2 + uz^2 + ...)
In 2d this looks like this:
|u| = root(ux^2 + uy^2)
where uy/ux gives us the tangent of the angle of vector u to the x'x axis:
tan a = uy/yx
So, the only thing that changes now in tasks is that the position is also being given as an function or that the position is not only a specific value of one axis, but is a point in 2 or 3-dimensional space!
Acceleration vector
Acceleration in 2 or even more dimensions is being described by the same exact way as before, but now clearly is an "vector".
The average acceleration is:
a avg = Δu/Δt = u2 - u1 / t2 - t1
that is the exact same equation we had in 1 dimension.
The instantaneous acceleration is:
a = lim Δt -> 0 (Δu/Δt) = du/dt
that is also the same as before
Well, then why bother?
The thing that now changes is that we can get into acceleration in each dimension separately, which means that the acceleration can be described by:
a = dux/dt i + duy/dt j + duz/d k + ...
or even:
a = ax i + ay j + az k + ...
where:
ax = d^2x/dt^2
ay = d^2y/dt^2
az = d^2z/dt^2
etc..
that is the second derivative of position with time.
The actual meter can again be found using the root-equation.
Full-On Example
Suppose the position with time is given by the following equations:
x = 3 + 2t^2
y = 10t + 0.25t^3
a) Where is the object at t = 2seconds?
b) Calculate the change of position and average velocity at the range of t = 0s to t = 2s
c) Write an equation that describes the velocity with time and find the velocity at t = 2s
d) Calculate the average acceleration at the range of t = 0s to t = 2s
e) Write an equation that describes the acceleration with time and find the acceleration at t = 2s
a)
At t = 2s the object is at:
x = 3 + 2*2^2 = 10m
y = 10*2 + 0.25*2^3 = 22m
So, r = 10i + 22y and the meter is:
|r| = root(x^2 + y^2) = root(10^2 + 22^2) = 24.6m
b)
For t = 0 we have that:
r0 = xi + yj = (3+2*0^2)i + (10*0+0.25*0^3) = 3i + 0j
For t =2 we have that:
r2 = xi + yj = (3+2*2^2)i + (10*2+0.25*2^3) = 11i + 22j
So, Δr = r2 - r1 = (11-3)i + (22-0)j = 8i + 22j
The average velocity is:
u avg = Δr/Δt = 8u + 22j / 2 - 0 =>
u avg =4i + 11j
where ux avg = 4m/s and uy avg = 11 m/s
c)
The component vectors are:
ux = dx/dt = 2*2t = 4t
uy = dy/dt = 10 + 0.25*3*t^2 = 10 + 0.75t^2
So, the instantaneous velocity is:
u = 4ti + (10 + 0.75t^2)j
At t = 2s we have that:
u2 = 4*2i + (10 + 0.75*2^2)j =>
u2 = 8i + 13j
and the value is:
|u2| = root(8^2 + 13^2) = 15m/s
with tan a = ux/uy = 13/8 => a = ~58 degrees
d)
To calculate the average acceleration we have to find the value for each component vector and so for each dimension separately.
ax avg = Δux/Δt = 8 - 0 / 2 - 0 = 4 m/s^2
ay avg = Δuy/Δt = 13 - 10 / 2 - 0 = 1.5 m/s^2
e)
The acceleration equation can be found by finding each dimensions equation using differentiation.
So,
ax = dux/dt = 4 m/s^2
ay = duy/dt = 0.75*2t = 1.5t m/s^2
So, the equation for acceleration is:
a = 4i + 1.5tj
At t = 2s we have that:
ax2 = 4 m/s^2, cause it's static
ay2 = 1.5*2 = 3 m/s^2
So, a = 4i + 3j and the meter is |a| = root(ax^2 + ay^2) = root(4^2 + 3^2) = 5 m/s^2
We can also calculate the angle to x'x that is:
tan b = 3/4 => b = ~37 degrees
And this is actually it for today and I hope you enjoyed it!
Next time we will get into missile or bullet motion, that is one of the basic plane motions (the other one being circular motion) that you have to know to understand 2-dimensional physics!
See ya soon...Bye!
Hii drifter
Hello,
I see you are new here!
Welcome to Steemit!
I hope you enjoy your stay :)
Hi i am new here nice to meet you
Good luck my friend @drifter1
thanks :)
I'm waiting for the next part of you post, more physics in steemit!
Great article it is always nice to find someone with same interest.
I guess you will mostly focus on Mechanics? Or will other topics follow as well?
Thanks,
I guess I will first finish of Mechanics to have a nice flow in my posts.
But I'm also thinking of getting into Electromagnetism, Thermodynamics, Relativity and even more branches in the future!
Automation of those equations and theorems in code is in my to do list as well..
:)
Glad you enjoy Physics as well...
I wrote a bit about special relativity (basic stuff) and I will try to write about other topics as well. I guess I will publish the last part of my special relativity text in the coming days and then write about electrics/electrodynamics. It would be amazing if you would maybe look other my posts and give me some constructive criticism.
Wohw, thanks for taking the time to write all this. Steemit turns into a library of knowledge thanks to work like yours!
I thank you for your beautiful comment :P
Nice to see people enjoying my work!
postingan mu sangat bermanfaat sekali
saya suka dengan postingan mu
saya akan tertarik dengan postingan mu yang lain
good luck salam kenal dari saya