Physics - Classical mechanics - Smooth Circular motion
Hello it's a me again drifter1! Today we continue with Physics and more specifically Classical Mechanics by getting into yet another plane motion. The smooth circular motion is one of the most basic 2-dimensional motions. This post is about everything you need to know about this kind of motion. So, let's get started!
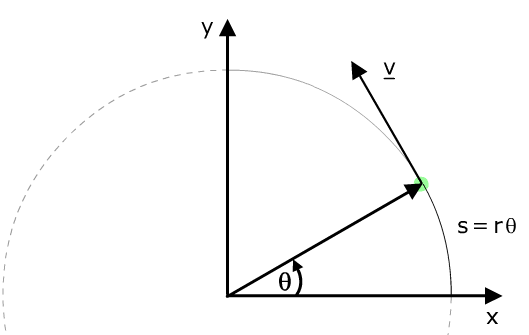
Getting into Circular Motion
In projectile motion last time, we analyzed each motion independently and separately.
We found out that:
- the y-axis follows a free falling motion, if the gravity is supposed constant
- the x-axis follows a constant velocity motion, if the air resistance is non-existent.
For circular motion we will not separate each motion, but follow another approach:
Using polar coordinates we have:
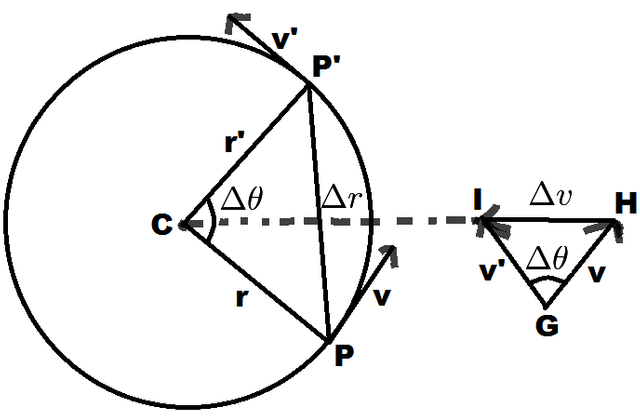
- Δθ angle between two velocities
- Δu velocity change where the meter of velocity is constant
- Δr displacement when going from the start to the end point
- r radius that is the same for each point
Angular acceleration
The triangles CPP' and GIH are "similar" cause they are both isosceles triangles (two sides are equal to radius) and have the same angle Δθ.
Therefore the ratio of their corresponding sides is equal and so we have:
|Δu|/v = Δr / r => |Δu| = v/r * Δr
We know that the average acceleration is equal to a avg = |Δu|/ Δt.
By replacing |Δu| with the upper equation we end up with:
a avg = u/r * Δr/Δt
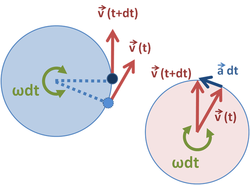
From the limit of Δt -> 0 we can find the instantaneous acceleration which is:
a = lim Δt -> 0 [u/r * Δr/Δt] =>
a = u/r * lim Δt -> 0 [Δr/Δt].
The limit is now actually the velocity u at the point P and so:
a rad = u^2 / r
which is the ratial or angular acceleration at any point.
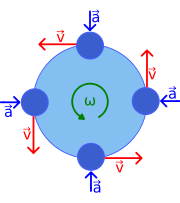
Note that the angular acceleration "goes inward" at any point, cause it "turns" the object.
Angular velocity
For circular motions we also define something called a period T which is the time needed to do a whole circle. Because, we are talking of an circle the distance traveled in a whole period is equal to 2πr that is the the circumference of an circle.
Therefore the velocity at any point is now:
u = 2πr / T
We sometimes also use another kind of velocity called angular velocity that tells us how many radians/sec we are travelling at.
The angular velocity that is mostly noted as ω is:
ω = Δθ /Δt = 2π / T = 2πf
where f = 1/T is called frequency.
By using the angular velocity we can now define the velocity as:
u = ωr
And so the angular acceleration becomes:
a rad = ω^2*r = 4π^2r / T^2 = Δω / Δt
Examples:
1.
Suppose an object has an constant velocity meter of 45m/s.
The angular acceleration has a maximum meter of 8.9 m/s^2.
Which is the smallest radius that the object can circle through?
By using the simple equation for angular acceleration we get:
a rad = u^2 / r =>
r = u^2 / a rad =>
r = 45^2 / 8.5 =>
r = 230 m
That is the smallest radius, cause the angular acceleration and radius are inversely propotional.
2.
An object's motion follows a circle with a radius of 5m, and does a circle in 4s.
Which is the acceleration of that object?
Because it does a circle in 4s the period is T = 4s,
By using the equation for velocity that contains the period and radius only we end up with:
u = 2πr / T =>
u = 2π*5/4 =>
u = ~7.9 m/s
So, the angular acceleration is:
a rad = u^2 / r =>
a rad = 7.9^2 / 5 =>
a rad = ~12 m/s^2
Image Sources:
And this is actually it for today!
Next time in Physics we will get into some exercises in plane motion (projectile and smooth circular).
I'm also setting up everything for the compiler project and the next post should be ready soon!
Bye!
Thank for information...
Please upvote my post...