Physics - Electromagnetism - Capacitors (Condensers) and Capacitance
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into Capacitors and Capacitance.
All the mathematical equations will be drawn using quicklatex!
So, without further do, let's get started!
Capacitor (Condenser)
Until now we covered how electric force is applied to charged particles from the generated electric field around a distribution of charge. We talked about electric flux and potential that help us solve problems that contain electric fields.
But, one thing still remains...
Is there a way to store the electric potential energy in some "device" so that we are able to use it later on?
Of course there is and we actually (almost) covered it already, but just without specifying an exact name for it! Remember electric dipoles?
Any set of two electrical conductors that are separated by a "special" insulator or even "air" is called a capacitor (or condenser). Most times these two conductors have the same magnitude of charge, but are oppositely charged (like electric dipoles) which means that the total charge of the two conductors of the capacitor is zero.
I will talk only about this general type of capacitors!
When saying that a capacitor contains a charge Q we will of course mean that one will have charge +Q, whilst the other one will have a charge -Q.
Two parallel conductive plates generate the following electric field:
This is the most common type of capacitor used!
Capacitance
All the stuff that we talked about till' now is of course proportional to the charge Q and so if we double the charge of each conductor we will of course also double the electric field and potential difference between those conductors. But, this means that the quotient of charge to potential difference (and also the opposite) is not changing! This exact quotient describes the capacitance of a capacitor.
The capacitance C of a conductor is the quotient of the magnitude of the charge Q of any of the two conductors it's build up by the magnitude of the potential difference V between those conductors.
The equation for capacitance is:
In the SI system Capacitance is calculated in Farad (F) which of course is:
In circuit diagrams a capacitor is noted by the following symbol:
Capacitors are used a lot in electronic devices and those devices could not exist without them. It's very important to have some way of storing electrical energy.
Calculating capacitance
As already mentioned before, the most common type of capacitor has two parallel conductive plates.
Let's say that each of them has an area A and that they have a distance d which is very small compared two the sizes of the plates.
The electric field of such a capacitor is mostly concentrated between those two plates.
There is still an electric field outside of the limits of the conductors, but when the distance is very small i's negligible.
That way the electric field between those two plates is uniform and the charge is uniformly distributed along the surfaces of the two facing sides of the conductors.
In an application that we covered previously during this series, we proved that the electric field can be calculated using the following equation:
where σ is of course the area density of charge.
The area density σ is calculated using:
When having a uniform electric field between two parallel plates we have proven that:
Using this equation we end up with this equation for potential difference:
Substituing Vab into the capacitance equation we get:
where ε0, A and d are of course constant for any capacitor.
This proves that the capacitance is constant and doesn't depend on the charge of the capacitor. And so the capacitance is proportional to the Area and inverse proportional to the distance of the plates.
This last equation also tells us that capacitance can also be calculated in C^2/J, where 1J = 1 N*m.
That way ε0 can now also be described in:
This is what we will use for problems around capacitors...
Also remember that for all these calculations we specified "empty" space between the conductive plates. When having an insulator (or dielectric as we will call them later on) the calculations are of course different, but don't worry we will get into those capacitors some posts later on!
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
And this is actually it for today!
Next time we will get into how we solve problems that contain Capacitors!
Bye!

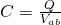
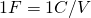
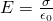
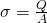
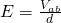
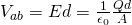
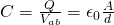
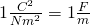
UpVot me please
Me too please!
Me too me too! :D
PS: I have no clue what this joke is about :D
Hahahhaa
Since you're handing out all these upvotes, I guess I'll give you a few as well. ;) Nice post by the way, I think it deserves some #love.
Hey! Hey! Me too! Me too!
Hi @drifter1!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Please please please upvot me