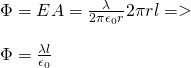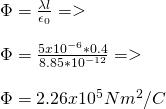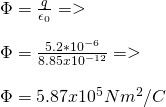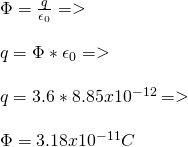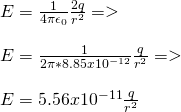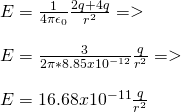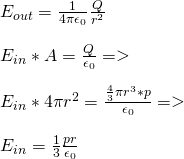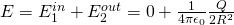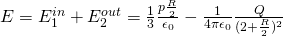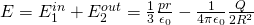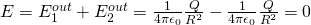Physics - Electromagnetism - Electric flux exercises
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into exercises around Electric flux!
I highly suggest you to read the previous posts of this series that talk about Flux, Gauss's law and applications of Gauss's law, cause else you will just see formulas/equations being applied and will not understand the concepts behind it!
So, without further do, let's dive straight into it!
Electric Flux
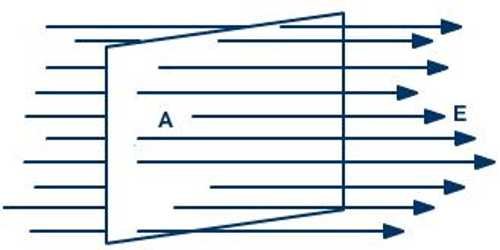
Just to start easy, let's first get into a simple example of Electric flux!
Suppose we have a very thin cylinder of radius r = 0.16m and length l = 0.4m.
Along the axis of the cylinder there is an infinite length positive charge with linear charge density λ = 5μC/m.
Knowing that the electric field of this charge is E = λ/2πε0r, calculate:
a) The electric flux that passes through the cylinder
b) The electric flux that passes through if it had a larger radius of r' = 0.32m
c) The electrix flux that passes through if it's length was increased to l' = 0.8m
Electric Flux is calculated using:
Φ = EA
The area of the side of the cylinder is:
A = 2πrl
The bases don't play a role (vertically across to the field) and so this is the area that we will use in our equation...
That way:
a, b)
We can see that the radius cancelled out and so the results for a), b) are clearly the same, something that we already explained in a previous post, by saying that the electric flux is independent of the radius of a sphere and so also of a cylinder...
So, the electric flux that passes through the cylinder with any radius is:
c)
Having the length multiplied by 2 (l' = 2l) and by seeing in our flux equation that the flux is proportional to the length we can already imagine that the flux will be double that of a) and b).
So:
Gauss's law
One of the things that Gauss's law states is:
Φ = q/ε0
And so when applying Gauss we want to find either of these:
- The flux when knowing the charge
- The charge when knowing the flux
Let's get into an example for each...
1.
A closed surface encloses a total charge of q = 5.20μC.
Calculate the total electric flux that passes the surface.
By using the formula of Gauss we get:
2.
The electric flux that passes a closed surface is 3.6 Nm^2/C.
How much charge is enclosed by this surface?
By again using Gauss's formula we get:
Applications of Gauss's law
To make it more interesting let's get into stuff that uses the formulas we talked of in the applications of Gauss posts, but more advanced...
1.
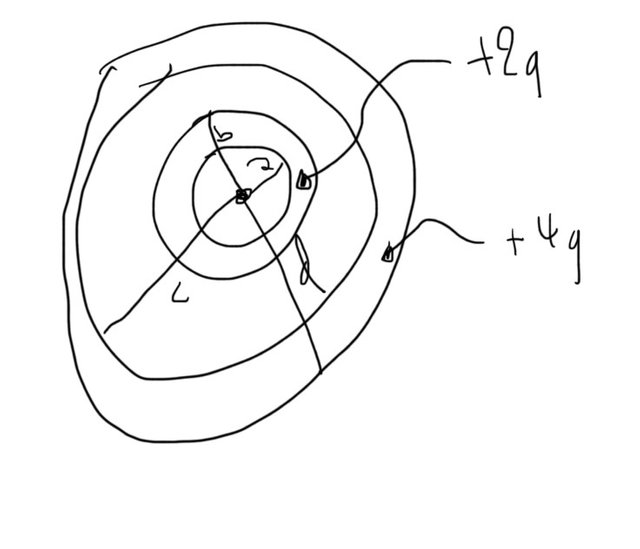
A small conductive sphere cortex with inside radius a and outside radius b is coaxial with a larger sphere cortex of inside radius c and outside radius d.
The small sphere has total charge +2q, while the larger sphere has a total charge of +4q.
Calculate the electric field at a radial distance r away of the center of those sphere cortexes as a function of q and r, where:
i) r < a
ii) a < r < b
iii) b < r < c
iv) c < r < d
iv) r > d
The scheme looks like this:
professional digitizer drawing by myself xD
i)
When r < a then the Gaussian surface doesn't enclose any charge and so:
Φ = Q/ε0 = 0
which means that the total electric field is also E = 0!
ii)
When a < r < b then the Gaussian surface is inside of the small sphere cortex.
Because of electrostatics we know that the total electric field inside of a conductor is zero.
And so E = 0 again.
iii)
When b < r < c then we are in a "vacuum" and so there is an electric field that can be found by using Coulomb's law!
This electric field is of course caused by the "small" charge +2q.
That way:
iv)
When c < r < d then we are in a similar case to ii), cause the electric field inside of the large sphere cortex is of course again zero.
That way E = 0.
v)
When r > d then we are in a similar case to iii), but will also include the charge of the outer (larger) sphere.
This means that the electric field now is:
We can do the "same" with coaxial cylinders!
Try on your own!
2.
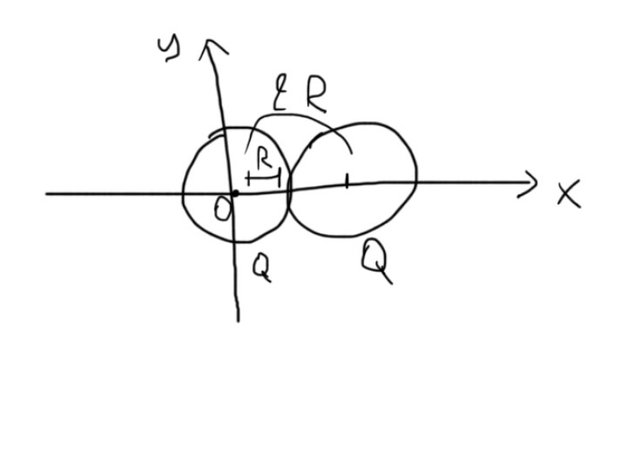
A positive charge Q is uniformly distributed (density p) along the surface of each of two conductive spheres of radius R.
One has the origin point O(0, 0) as a center, while the other the point x = 2R.
Calculate the electric field (meter and direction) at the points:
i) x = 0
ii) x= R/2
iii) x = R
The schema looks like this:
Professional art by myself :P
The total electric field is equal to the vector sum of the fields generated by each sphere on it's own.
E = E1 + E2
For each charged sphere we know:
which are the electric field going in and out for each sphere.
i)
When x = 0:
Because the electric field of the first sphere is zero and the point is "outside" of the second sphere...
Of course that means that the electric field goes in the -x direction!
ii)
When x=R/2:
Cause the point is inside of the first sphere and outside of the second one.
I put a minus on the second one to point out that the result gives us a +x direction.
When this "minus"-part is larger then the direction is of course to the left!
iii)
When x = R:
Because the point is exactly at the center of those spheres which means that the electric field generated by both is equal, but opposite and so cancels out!
We could continue on with a point inside of the second sphere or even a point outside of the second sphere, but to the "right" direction. In both cases we would have the "outside" field of the first sphere. When inside of the second we would use the "inside" field, while when outside the "outside" field.
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
And this is actually it for today and I hope that you learned something!
Next time we will start getting into potential energy!
Bye!