Physics - Classical Mechanics - Rectlinear motion with constant accelaration and free falling
Hello its a me again drifter1! Today we continue with Physics and more specifically the Classical Mechanics branch by getting into rectlinear motion with constant acceleration and also free falling! I suggest you to read my previous post about rectlinear motion velocity and acceleration that you can find here, cause else you will have trouble understanding! So, without further do, let's get started!
Rectlinear movement with constant acceleration
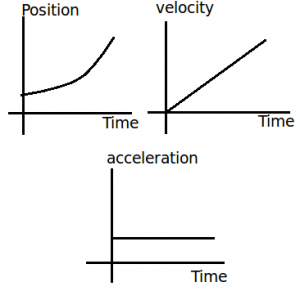
Using the equations from the last post and by having a constant acceleration, we end up with a linear motion with smooth change in velocity that is exactly the same in each second. This means that we have the same du/dt for any time interval and that way we end up with simple linear equations for velocity, acceleration and position in time.
When the acceleration is constant the following applies:
a = (u - u0) / (t - 00 => u = u0 + at (instantaneous velocity)
u avg = u0 + u / 2 => u avg = 1/2(u0 + u0 + at) => u avg = u0 + 1/2 at (average velocity)
and because the average velocity also equals u avg = x - x0 / t we have that:
x- x0 /t = u0 + 1/2 at => x = x0 + u0t + 1/2 at^2 (position in time)
Two other equations that we can get by doing some calculations on the upper equations that are very useful in some cases are the following:
u^2 = u0^2 + 2a(x - x0) (an equation that doesn't contain time!)
x - x0 = 1/2 (u0 + u) t (an equation that doesn't contain acceleration!)
The first one is useful when we don't know the time and the other one if we don't know the acceleration!
Example:
Suppose an constant acceleration a = 4m/s^2
The center of the axis is at x = 0.
At the position x0 = 5m and at time t = 0s we have a velocity u0 = 15 m/s.
1. Find the position and velocity at t = 2 sec.
2. How far away of the center will the object be when it reaches a speed of 25 m/s?
1.
The first is pretty simple and we will use the two basics equations.
x = x0 + uot + 1/2 at^2 = 5 + 15*2 + 1/2*4*2^2 => x = 43 m
u = u0 + at = 15 + 4*2 = 23 m /s
2.
For the second one we will use one of the "other" equations, cause the time is unknown.
u^2 = u0^2 + 2a(x - x0) =>
25^2 = 15^2 + 2*4*(x - 5) =>
x = 55m
We could also find the time first and then the position, but using this other equation is much faster!
Object free falling
Free falling can be described approximately by an rectlinear motion with constant acceleration, if we suppose that the gravity acceleration or the drag of the earth is constant and the same at every second. The gravity acceleration or acceleration of free fall is being symbolized by g and equals 9.8 m/s^2 on earth and 1.62 m/s^2 on the moon. These are the values that we will use in any example from now on and they are mostly given to us and sometimes get approximated even more by saying that the drag of the earth is equal to 10 m/s^2 for example!
Example:
Suppose an object is falling from an 50 m height to the ground. The velocity at t=0, where x0 = 50m above ground is v0 = 0.
1. Find the velocity and height the object is at t = 1s
2. Find the velocity and time where the object has fallen 20 m
3. Find the velocity and time right before it touches the ground (0m above the ground)
By thinking of the free fall as a constant acceleration motion with a = g = 9.8 m/s^2 we can use the same equations as before to answer the questions.
1.
x = x0 t + 1/2(-g)t^2 = 0*1 + 1/2*(-9.8)*1^2 = -4.9 m
Note that we use -g, cause gravity here pushes us down.
This means the height at t = 1 is 50 - 4.9 = 45.1 m
By using the simple equation for velocity we end up with:
u = u0 + at = 0 + (-g) t = -9.8 * 1= -9.8 m/s
2.
The time is unknown and so we will use the "no-time" equation:
u^2 = u0^2 + 2(-g)(x - x0) =>
u^2 = 0 + -9.8*2(-20 - 0) =>
u^2 = 392 =>
u = ~ 19.79 m/s
Which means that the velocity is - 19.79 or 19.79 going down!
By using the simple velocity equation:
u = u0 + (-g)t => -19.79 = 0 -9.8*t => t = ~2.02 s
3.
Because the time is unknown we will use the same exact equation as before to find velocity:
u^2 = u0^2 + 2(-g)(x - x0) =>
u^2 = 0 + 2(-9.8)(-50 - 0) =>
u^2 = 980 => u = ~ 31.3 m/s
and so -31.3 m/s, cause the velocity is pointing down!
By using the velocity equation we calculate the time it will hit the ground:
u = u0 + (-g)*t => -31.3 = 0 -9/8*t => t = ~3.19 s
And this is actually it for today!
Next time we will get into integration of velocity or acceleration to find the position or velocity.
Bye!