Physics - Classical mechanics - Dynamics of Circular motion

    Hello it's a me again drifter1! First of all, I want to point out that we reached 500 followers and I want to thank you all for your support! Today we continue with Physics by getting into more specific things of circular motion dynamics and applications! We covered a lot of things in the post about smooth circular motion here. If you haven't checked it don't worry at all, cause I will make a small recap/introduction first to give you the basic knowledge needed! So, without further do, let's get started!

Recap

    In my post about smooth circular motion we said that it is a 2d or plane motion, where we don't separate the movement for each axis like in projectile motion, but follow another approach.

    We suppose that the velocity is constant in meter (value) but changes direction all the time in a perfect circle! That way we can use the simple equations of linear motion.

Using polar coordinates (angle θ, radius r) we end up with an angular acceleration:

a rad = u^2/R

    This can be easily proven by triangle "similarity", using a avg = |Δu|/Δt and finding the limit to Δt -> 0. I covered it in my post!

The velocity is calculated using:

u = 2πr / T

where 2πr is the circumference of a circle and is the period or time taken to do a full circle.

You can clearly see that we use the basic x = ut => u = x/t.

Because of t = x/u the period can be calculated using:

T = 2πR / u

The angular velocity is noted as ω and looks like this:

ω = Δθ / Δt => ω = 2πf = 2π / T

    So, angular velocity is how many radians (other term for degrees where 2π rad = 360 degrees) per second we are moving. It's calculated in rad/s.

That way another equation for angular/radional acceleration is:

a rad = 4π^2R / T^2

So, angular acceleration is calculated in rad/s^2.

Circular motion Dynamics

Here we are now to apply Newton's laws to see what we can get from it.

It is very clear that the object is not at rest, but also doesn't move in a constant linear motion.

    So, because the velocity changes direction there is a force applied to the object and Newton's second law applies. 

This means that ΣF != 0 and by using the angular acceleration we end up with:

ΣF = m * a rad =>

ΣF = m * u^2 / R

    The force that makes the object follow a circular path is always applied to the center of the circle and always has a constant meter (value). Because it's applied to the center we call this force the centripetal force (Fc) and because of that a rad is also called centripetal acceleration (a c).

Don't fall into the trap thinking that the centripetal force Fc is a part of ΣF! It's ma!

This will help you when drawing the free-body diagram!

Applications

 Circular dynamics are used in the following:

• Conical Pendulum
• Horizontal (flat) curve/turn
• Inclined or banked (with degree) curve/turn
• Vertical circle

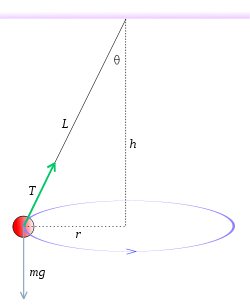
A conical pendulum looks like this:

Which is the force of the thread (tension) when the sphere is moving with a "constant" velocity u?

By analyzing the horizontal and vertical component vectors of the tension we end up with:

T * sinθ = m u^/R    (2nd law)

and

F cos θ = mg    (1st law)

By diving the two equations we end up with:

tanθ = u^2/gR (1)

The radius R = L * sinθ and so the circumference is 2πL sinθ. 

That way:

u = 2πL sinθ / T (2)

Using those two equations (1 and 2) we end up with:

cosθ = gT^2 / 4π^2L

which gives us the thread tension:

T = 2π root(Lcosθ / g)

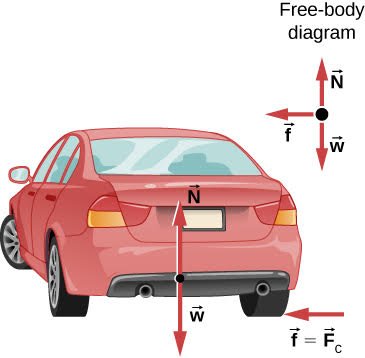
The horizontal/flat curve motion of a car into a corner comes next!

Here the friction of the tires and the ground (with a friction factor μs) is used!

Let's find the maximum velocity so that the car doesn't drift into the corner!

I waited for ages to say that

Supposing that the car doesn't drift into the corner (no slipping) we have:
F = m u^2/R

and

N - mg = 0

    where F is the friction and the only force that turns the car and N is the vertical ground force (action/reaction).

Because the maximum friction is F = μs * N = μs * mg we have:

μs * mg = mu^2 / R =>

u = root(ms * g*R)

which is the maximum velocity we can travel at for a specific radius R and a "slip" factor μs.

Now let's get into banked curves that look like that:

Suppose that we want to find the degree θ of the slope so that there is no friction needed!

    The vertical ground force N now has a degree θ to weight force and so we find the components and use the 1st and 2nd law again like before.

N * sinθ = mu^2 / R    (2nd law)

and

N * cosθ - mg = 0    (1st law)

By diving the two equations we end up with:

tanθ = u^2 / gR =>

θ = arctan(u^2 / gR)

This is the degree needed for a constant velocity u with a radius R slope turn.

For the vertical circular motion I did some great examples at the end of this post!

The centripetal force Fc = mu^2/R must be "constant".

This means that there must be a upward force Ft at the top so that:

Ft - mg = - mu^2 / gR =>

Ft = m(g - u^2/R)

In the same way there must be a upward force Fb at the bottom so that:

Fb - mg = + mu^2 / gR =>

Fb = m(g + u^2/R)

The force Ft is smaller then the weight and the force Fb is greater then the weight!

Image Sources:

https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcSene2pYQuwvyIjI3HTkDH-7Q5Xj-VenXgzaSEQ5tE1LW-mc9TC2A

https://qph.fs.quoracdn.net/main-qimg-93da58735e7ec7e183d99f52cc4018a6

https://upload.wikimedia.org/wikipedia/commons/thumb/5/53/Conical_pendulum.svg/250px-Conical_pendulum.svg.png

https://cnx.org/resources/3b9073156ddf0f5f8e6fe674990b44228050b7cc/unnamed.jpg

https://i.stack.imgur.com/a7CAm.jpg

https://www.physicsforums.com/attachments/yf_figure_05_76-jpg.130139/

And this is actually it for today!

From next time on we will start getting into examples and exercises!

Bye!