Physics - Electromagnetism - Electric dipoles

Source

Introduction

Hello it's a me again Drifter Programming!

    After covering Electric fields we can now continue on with Physics and more specifically Electromagnetism to talk about Electric Dipoles, that create an unique electric field.

So, without further do, let's get straight into it!

Electric dipole

    Suppose we have 2 point charges q1 and q2 that have the same amount (meter) of charge, but of opposite sign. This means that q1 for example has a charge +q, while q2 has a charge -q. This exact combination of charges is called an Electric dipole! Let's also say that the distance between those charges is d.

Now there are two questions that need to be answered:

1. What kind of forces (F) and torques (τ) are applied to a dipole when it's inside of another electric field?
2. What kind of electric field does it create/generate?

Let's answer each one by it's own starting of with the first one.

Electric dipole torque and potential

Let's put a dipole inside of an uniform electric field E.

Source

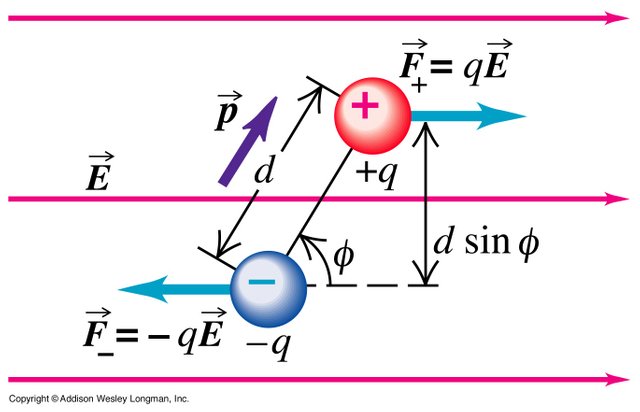
    The forces F+ and F- of course have the same value/meter qE, but also have an opposite direction and so cancel each other out!

We can see that:

The total force applied to an electric dipole inside of an uniform electric field is zero.

    But, those forces are not going to the same direction which means that the total torque is not zero! [Torque is something that we will cover later on in Classical mechanics, but just so that you understand it now think of it as "something" that makes objects rotate.]

    Anyway, supposing the angle between the uniform electric field E and the axis of the dipole is φ and by also including the concept of electric dipole torque as p = ql (in C*m) we have that the torque is:

quicklatex

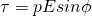
Or by using an more general vector form we could say:

τ = p x E

Because of this cross product we have that:

• the torque is maximum when p and E are vertical across (φ = π/2)
• the torque is zero when p and E are parallel (φ = 0 or π)

The torque always tries to rotate the dipole so that it gets parallel to the uniform electric field!

By doing so the torque does a Work (also something that we will cover later in Classical mechanics):

quicklatex

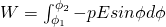
    Because W = U1 - U2 (also something that we will cover later on) we have that the electric potential is:

U(φ) = -PEcosφ

or

U = -p*E

in vector form

And so:

1. the potential energy is minimum (maximum negative) when φ = 0
2. the potential energy is maximum when φ = π
3. the potential energy is zero when φ = π/2

    When the electric field is non-uniform then the dipole will also have a force applied to it, which means that it will move to some direction. So, an object with zero sum of charge, but dipole torque (q*l) will have a force applied to it when inside of an non-uniform electric field!

    In exercises of dipoles we of course will use those equations, but because it's more Classical mechanics then Electromagnetism I think that I will not get into many examples :)

Electric dipole field

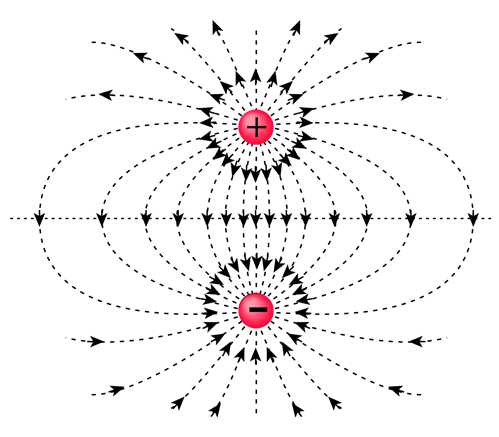
Lastly, let's also get into how such a dipole electric field looks like!

The following is an electric dipole field:

Source

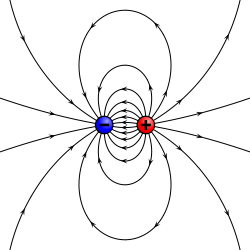
    As mentioned in my previous post we make the electric field lines go from positive to negative charges. But, here you can also see that because the charges are equal we also have an equal distribution of the field.

    At each point of this electric field E the total electric field is the vector sum of the fields E+ and E- created by the charges q+ and q- individually.

But, how do we calculate this field?

    Well, let's get into a simple example where we calculate the electric field of an dipole that is on-top of the y-axis at a point P at (0, y)

    Supposing that the point P is at y and that the center of the dipole is at O (0, 0) having the positive "pole" be at d/2 and negative "pole" at -d/2 we have:

quicklatex

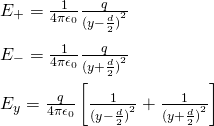
Because y is much larger then d we can approximately get the simpler equation:

quicklatex

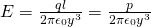
    Of course if the point P was not at some axis (y or x) then the mathematical equations would become more complex, but I guess that you got an idea of how we calculate them :)

    Well, a lot of this stuff was not covered yet in Classical mechanics and so I suppose that someone will understand this post better if he/she already knows the concepts of work, energy and potential. But, don't worry you can get back to it after I cover it in Classical mechanics if you have problems at the moment :)

Previous posts about Physics

 Intro

Physics Introduction -> what is physics?, Models, Measuring

Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P) 

Classical Mechanics

Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those

Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall

Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity

Rectlinear motion exercises -> examples and tasks in rectlinear motion

Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion

Projectile motion as a plane motion -> missile/bullet motion as a plane motion

Smooth Circular motion -> smooth circular motion theory

Plane motion exercises -> examples and tasks in plane motions

Force and Newton's first law -> force, 1st law

Mass and Newton's second law -> mass, 2nd law

Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction

Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications

Contact forces and friction -> contact force, friction

Dynamics of Circular motion -> circular motion dynamics, applications

Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications

Contact force and friction examples -> exercises in force and friction

Circular dynamic and vertical circle motion examples -> exercises in circular dynamics

Advanced Newton law examples -> advanced (more difficult) exercises 

Electromagnetism

Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization

Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples

Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines

And this is actually it for today and I hope that you learned something!

Next time we will get into Exercises/Examples for Electric charge, fields and dipoles :)

Bye!