Physics - Electromagnetism - Calculating electric potentials
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into how we calculate potentials!
I highly suggest you to read my previous post about Electric potential energy before-hand, but either way there will be a small recap in the beginning of this post, so that I remind you of the most important things!
So, without further do, let's get straight into it!
Quick recap of Electric potential energy
All the following is true, because electromagnetic forces are in the category of conservative forces and so create conservative force-fields!
The Work that is produced to q' from the radial force Fr (that is applied by a static point charge q), while a test charge q' moves from a point A to a point B is:
This Work is the same for any possible trajectory from point A to B!
This can be proven by using the following equation for non-radial points:
If we make a cycle and start from a point A and go to the same point A, in the end the work produced is zero!
By using these equation we can now say that the potential energy when moving along a distance r is:
This is also true for spherical uniform distributions of charge, cause from Gauss's law we know that such spheres behave like they have all the change concentrated in the center like a point charge.
The potential energy depends the point of reference, where we have U = 0.
U = 0 mostly when the distance between the charges q and q' is supposed infinite, r = ∞.
When having more charges then using the superposition principle the potential energy of a test charge becomes the following algebraic sum:
Some more stuff I don't featured last time
I already told you that the equation between two point charges also works for spherical uniform distributions of charge, because they act like point charges. But the thing is...we can represent any distribution of charge as a set of point charges and so the last equation that talks about many charges gives us the potential energy for any static electric field. Therefore any electric field that is generated by a static distribution of charges is a conservative force field! (Here you can see why all of the stuff we covered 'till now works)
Let's suppose we have the charges q1, q2, q3, ... that are placed with an infinite distance apart. Let's say that we move them so that the distance between qi and qj becomes rij. The total potential energy now is the sum of the interactions in pairs of two and so we can write:
This sum contains all the pairs of charges, but we of course don't let i equal j cause there can't be an interaction of a charge with itself! Also, when including i = x and j =y we will not include i = y and j = x, cause this pair was already in the sum. And so this sum is true for all the i's and j's for which i > j.
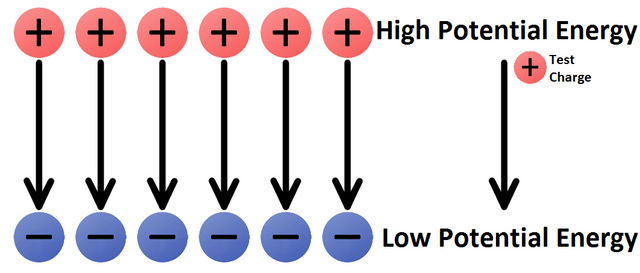
We described the Work and potential energy using a charged particle that moves inside of an electric field. When a charged particle moved from a point A to a point B, the Work was W = Ua - Ub, and so when Ua is greater then Ub, the electric field produces positive work to the particle. During that the particle "fell" from a point of greater potential energy to a point of lesser potential energy!
Another way of describing it is using an external force Fext that acts on the displacement a -> b and saying that the Work of this force is equal to the "opposite" displacement b->a and so equal to Ua - Ub! We mostly don't use this concept!
Electric potential
First of all, don't confuse electric potential with electric potential energy!
Electric potential describes the electric potential energy per charge unit.
And so we now get into the concept of electric potential or more simply potential!
The potential is:
- very helpful when calculating the potential energy of charged particles
- mostly easier to calculate, which helps us when calculating electric field
We define the potential V at each point inside of an electric field as the potential energy U that is connected with a test charge q' at this point, through the charge q' as:
Potential energy and charge are both scalar units and so does the potential.
The metric of potential is of course energy/charge and so in the SI system 1 J/C or 1 Volt (V), in honour of the Italian scientist Alessandro Volta.
In electronic circuits potential is mostly called Voltage!
Let's also define the concept of work per charge unit by dividing W = Ua - Ub with q'.
The equation now becomes:
where Va = Ua/q' is the potential energy per charge unit at the point a and Vb the same for the point b. And so Va and Vb are the potentials of the points a and b individually.
To find the potential V at a point where a set of point charges act on we divide the algebaic sum we had before (for calculating the potential energy caused by more then one charges) with q' and so get:
When having charge distributions along lines, surfaces or volumes we then have to split this charge in many small charge elements dq and so the sum becomes the integral:
where r is the distance from the charge element dq to the point where we calculate the potential V.
When a set of point charges is given to us then the sum gives us an easy way of calculating the potential V. But, in many problems the electric field E is given or easy to find and so we can work with the field directly!
The force F that acts on the test charge q' can be written as F = q'E, and so the Work is:
If we combine this with the equation of work per charge unit we get:
When the electric field E produces positive Work to a positive test charge that moves from a to b, then the potential of a must be larger then b. Or by using the external force concept we could also say that a force per unit equal to -E would be needed to move the charge from b to a. The work that is produced by this external force is the electric potential difference:
By comparing this equation with the previous one we can see that we have an opposite sign, but also opposite integration limits and so from Mathematical analysis both are equivalent representations!
The difference Va - Vb is called "the potential of a as to b" or "electric potential difference between a and b". We sometimes write it as:
The potential is of course independent of the test charge q'. When a positive test charge moves from a higher to a lower potential (Va > Vb) then the electric field produces positive work.
Those points are undefined and we have to choose a "good" reference point of zero potential.
Positive charges tend to "fell" from a higher state of potential to a lower one, while negative do the opposite!
To calculate this potential difference in circuits we use a voltmeter!
We will get into circuits later on...
Calculating electric potentials
So, I talked about some many ways of calculating it, but what do we have to use each time?
The calculations of potential mostly are in one of the two categories:
- When knowing the distribution of charge we use the sum for point charges (set of charges) or integral for more advanced distributions.
- When knowing the electric field then we use the equation with the potential difference by choosing a "good" reference point of zero potential.
Note that some problems might be a combination!
Some tips:
- Potential is simply potential energy per charge unit. (by understanding this sentence you can continue on much easier)
- To calculate the potential caused by a set of point charges we simply use the sum.
- When having an continuous charge distribution we have to find a way of splitting this distribution up in many very small elements that are expressed using coordinates. After that we use the integral with the correct limits for which the whole distribution will be contained.
- Beware of constants and variables in the integration!
- When an electric field is given or can be calculated using previous methods we discussed through-out this series, then it might be easier to calculate the Work done when a test charge is being moved from a point a to a point b using the potential difference equation.
- V can be set zero for any convenient point. For sets of point charges this is mostly infinity, but for other distributions (and mostly those that are infinite) it's better or important to set V equal to zero for some finite distance and so for some point b. (this is similar to the calculation of potential energy!) Of course using that the potential of some other point a (Va) can be easily found, cause Vb = 0.
- Potential, potential energy and charge are all scalar units and not vectors! Don't make the mistake and use potential components. What you can and must do is use components of the vectors E (electric field) and dl (small displacements) when using the equation of potential difference (I think this name really stands out xD).
I would like to get into applications, but I think it's better if we include it in the "exercises" post of this "part" of Electromagnetism!
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
And this is actually it for today and I hope that you enjoyed it!
Next time we will continue on with Equipotential surfaces and potential gradient!
Bye!
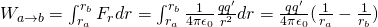
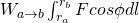
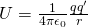
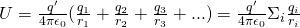
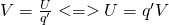
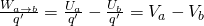
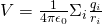
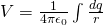
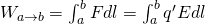
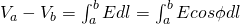
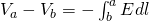
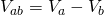
...feels like I just left a physics class; well detailed @drifter1
Thank you very much! Appreciated :)
That classroom feeling of... Do you understand and we will say yes sir because we want to end the lecture
Why is no one commenting.....i want to believe everyone understood that is why there is no comment...... Me too I don't have questions for now but sir this lecture is awesome
U will a make great physics Msc supervisor
Haha thank you! Appreciated, very much!
I'm actually a computer science student, but am really good at explaining what I learned (and still learn) during my studies...
I'm glad that so many people enjoy what I'm posting about and that I can define the theorems, mathematical equations, concepts of Physics, Mathematics etc. in a way that helps people understand them very easily!
The lectures in my university only helped me to understand the surface of all that I'm talking about in my articles, but learning all this stuff in-depth needed a lot of research in the internet, reading books, notes etc. which of course took a lot of time.
So, be sure that what I represent to you is what helped me understand and what I think will help all of you also when trying to understand Maths, Physics, Programming etc.
That's good.... I want to believe you are part of those students that sit in front of the class...
Let me come and be going
...lol
Everyone sure understood