Physics - Classical Mechanics - Velocity and acceleration in a rectlinear motion
Hello its a me again drifter1! Today we continue with Physics by starting out with a branch of Physics called Classical Mechanics that is all about Motion and Kinematics of Objects. More specificly we will start with Rectlinear motion and so motion in a straight line and talk about velocity and accelaration in such a "1-dimensional space". To understand the Vector stuff better, I suggest you to read my previous post about Vector Math first. So, without further do, let's get straight into it!
Classical Mechanics
Let's first start off with what Classical mechanics is all about. This physics branch is also called Newtonian Mechanics and is one of the two subparts of Mechanics, the other one being Quantum Mechanics. Classical Mechanics is all about motion and theories, laws that describe how an object moves and how it interacts with other objects using forces. So, this branch is trying to calculate the height a thrown ball will reach, how fast we need to throw it, how fast it will reach the ground and so on...
Rectlinear motion
But, motion is pretty complicated in 3d space, and to understand it better we will first get into Rectlinear motion. Rectlinear motion is the simplest of all motions, where an object moves in 1 dimension/axis and so in a straight line! Such simple physics is used if the rotation of an object is not important and only the actual movement from point A to point B.
Average Velocity
Whem an object moves from a speific point A to point B, where A has a coordinate of x1 and B a coordinate of x2 then we can find the average velocity using the following equation:
u avg = x2 - x1 / t2 - t1,
where t1 is the start time and t2 the "finish" time
Whenever we see a change in something we will symbolize it using a greek delta (Δ).
This means that x2 - x1 = Δx and is the change of position and t2 - t1 = Δt is the change in time.
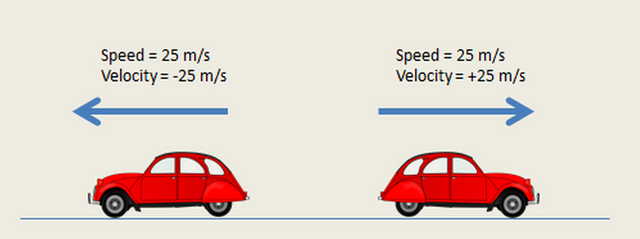
The change of time will always be positive (or will it? time travel!!!) and so the sign of velocity actually depends on if we go to the left or to the right and so if point A or point B comes first in the xx' axis.
Example:
Let's say we start of at t1 = 1 sec and at the position x1 = 19m and we end up at x2 = 277m at t4 = 4 sec.
The average velocity equals u avg = 227 - 19 / 4 - 1 = 86 m/s
Velocity describes how many meters per second we go and so here this value actually describes the average velocity or the constant velocity we need to have so that we need 3 seconds (Δt = 4 -1 = 3 ) to go from x1 to x2.
Instantaneous Velocity
Average velocity is nice, but what about the velocity at a specific time and so the instantaneous velocity? Well, you remember derivatives and limits? If we now take the limit of Δx/Δt for a specific Δt that goes to 0 then we end up with:
u = lim Δt -> 0 Δx/Δt = dx / dt
which is the instantaneous velocity.
This means that if we have a function for our position in time then differentiating it gives us the velocity in time function and that way we can calculate the velocity at any time and so any position!
Example:
Suppose t1 = 1s is the start time and t2 = 2s is the end time and that the position is being described by the function:
x = 20 + 5 t^2, where t is the time passed
For t = t1 and t = t2 we have the following results for x1 and x2:
x1 = 20 + 5*1^2 = 25m
x2 = 20 + 5*2^2 = 40m
So, the average velocity is:
u avg = x2 - x1 / t2 - t1 = 40 - 25 / 2 - 1 = 15m/s
The function that describes our velocity in time is:
u = dx /dt = x' = (20+5t^2)' = 10t
So, the instantaneous velocity at t = t1 and t = t2 looks like that:
u1 = 10*1 = 10 m/s
u2 = 10*2 = 20 m/s
The sign of that value depends on how we want to think about the system. If going to the right on the x axis means positive for us then the value of u1 and u2 is positive and so the velocity is "positive". If the value of our velocity was negative then we would have a "negative velocity" which actually means that we are going on the opposite direction.
Average Acceleration
Another important topic is the change in velocity and so accelaration! When the value is positive we are talking about acceleration and if it is negative we are talking about deceleration. The first means that the velocity is increasing and the second means that the velocity is decreasing.
The change in velocity divided by the change in time is equal to the average acceleration in that time period and looks like that:
a avg = u2 - u1 / t2 - t1 = Δu / Δt
where u1 is the velocity at t1 and u2 the velocity at t2.
Example:
If at t1 = 1s the velocity is v1 = 0,8m/s and at t2 = 3s the velocity is v2 = 1,2 m/s then:
a avg = 1,2 - 0,8 / 3 - 1 = 0,2 m/s^2
Which means that the acceleration is describing how many meters per second per second we are going and so how much the velocity increases or decreases at a specific time or time period.
Instantaneous Acceleration
Another way of describing acceleration is as the second derivative of the position, which means that we differentiate the velocity function again.
That way we then end up with the instantaneous acceleration that equals:
a = lim Δt -> 0 Δu / Δt = du / dt
And so a = du / dt = d/dt (dx/dt) = d^x / dt^2
Example:
If the velocity is described by u = 60 + 0,5t^2 then the acceleration is described by:
a = (60 + 0,5t^2)' = 0.5 * 2t = t
So, if t1 = 1s is the start time and t2 = 3s the end time we have that:
a1 = 1 m/s^2 and a2 = 3 m/s^2
And if we calculate the velocity v1 and v2 then:
v1 = 60,5 m/sand v2 = 64,5 m/s
which means that the average acceleration is a avg = 2 m/s.
If you look closer you will see that this value equals:
a avg = a1 + a2 / 2 = 3 + 1 / 2 = 4 / 2 = 2 m/s^2
And so we can calculate the average acceleration (and velocity also) by just adding the start and end acceleration (or velocity) and diving it by 2.
And this is actually it for today's topic and I hope that you enjoyed it!
Next time we will get into constant acceleration motion and free fall!
Bye!
Good post