Physics - Electromagnetism - Electric charge and field Exercises
Introduction
Hello it's a me again Drifter Programming!
Today we will get into examples/exercises that will cover everything that we covered about Electromagnetism 'till now. This means that this Physics post will contain examples about Electric charges, fields and dipoles!
I will of course split those examples into categories depending on the topic...
So, without further do, let's dive straight into it!
Electric charges and Coulomb's law
1.
Let's start simple...
Two equal point charges with charge +3μC have a distance 0.6m.
Find the meter of the force applied from one to another and also the direction of each force.
Answer:
We first convert the charge value into Coulombs which means that:
Using Coulomb's law we get:
Of course because the charges have the same sign we have repulsive forces and so the force applied from a to b goes in the direction a->b. The same for the other one...
2.
A negative charge q = -0.5μC applies an attractive force of meter F = 0.6N to an unknown charge that is 0.2m away. Find the unknown charge (meter and sign).
Answer:
Of course because the force is attractive we have opposite signs which means that the unknown charge will be of positive charge.
The meter can be got by using Coulomb's law with unknown "variable" the charge q'.
So,
3.
Suppose that we positively charge 2 spheres. When these spheres are at a distance of d = 40cm then the repulsive force has a meter of F = 0.25N.
Calculate the charges when:
a) The charges are equal
b) One sphere has double the charge of the other one
Answer:
The distance is of course d = 40cm = 0.4m.
a)
Supposing that each charge is q we can use Coulomb's law and find q like that:
which means that both charges have a meter q = 2.11μC
b)
Supposing that q' = 2q we have:
and so the charge have meters: q = 1.49μC and q' = 2.98μC
4.
Two point charges are on top of the x-axis.
q1 = +3nC at x = 0.4m
q2 = +5nC at x = -0.2m
Calculate the total force applied to an third point charge q3 = -8nC that is at x = 0.
Answer:
Of course both forces will be attractive cause q1, q2 are positive, while q3 is negatively charged.
Because of the superposition principle we of course can calculate each force separately and then get the vector sum of those two force vectors (which will be a substraction, cause the two forces will be of opposite direction).
The distances of q1 and q2 to q3 are equal to their position, cause q3 is at the center of the axis.
The charges are in nC and so we have to multiple each value by 10^-9 to get the correct metric.
That way:
Clearly the attractive force of q2 is "stronger" than the one of q1.
This means that the total force ΣF will "go to the left" and so in the -x direction.
The meter of that force is:
Electric fields
1.
Let's again start simple...
Calculate the electric field (meter and direction) at a point that is 0.5m away of an electric charge q = +4μC.
Answer:
By applying the formula with the correct metrics we get:
The electric field is of course "leaving" the source charge q and so points outwards.
For example if the point is at +x then the direction of the field would also be +x.
2.
Find the distance r of the point that is in the electric field of meter 6 N/C that is being generated of a charge q = 5nC.
Answer:
Of course we again just have to apply the formula to find the "missing variable" like that:
NOTE:
When the force and charge are known than we find the field using: E = F/q
3.
The following example is a mixup with Classical mechanics...
Suppose that we put an electron with:
- charge e = 1.6 x 10^-19C
- mass m = 9.1 x 10^-31kg
in between of two parallel charged metal plates that are 1cm apart.
The electromagnetic field created has a meter E = 10^4 N/C and goes upwards
Calculate:
a) The total force F that is applied to the electron
b) The velocity it will have after travelling a distance of 1cm, starting at rest.
Gravity is 9.8 m.s^2
Answer:
a)
Using the equation F = qE = eE we can find the electric force directly.
This means that the electric force applied to the electron is:
Force is calculated using F = ma and so the weight is W = mg.
This means that the weight applied to the electron is:
Of course the weight is a lot smaller then the electric force and so we can omit it for the calculations in b).
Because the electron is negativelly charged and the electric field E goes upwards the direction of the force F applied to the electron is downwards.
b)
Because the force goes downwards and is also constant we can use Newton's 2nd law.
By doing that we get the "downward" acceleration that the electron gets which is:
That's insane!
Think about how much force a car would need to have applied to get such an acceleration!
Anyway, by using the "no-time" equation (as I told it in Classical mechanics) we can find the velocity using only the acceleration and distance traveled.
The acceleration is "negative", but so does the distance and so:
I also wanted to get into an more advanced example that contains charge densities, but I think that the following link has you covered:
Electric dipoles
When talking about dipoles you just have to use the formulas I covered in my post.
But, let's get into a small application...
Suppose a dipole is inside of an horizontal uniform electric field of meter 5 x 10^5 N/C.
The charges of the "poles" are +-1.6 x 10^-19C and they are at a distance of l = 0.125nm, with '-' being on top and with an 35 degree angle to the electric field (that goes to the right)
Calculate:
a) The total force applied from the electric field to the dipole
b) The meter and direction of the dipole torque
c) The meter and direction of the torque
d) The potential energy at that position
Answer:
a)
In every uniform electric field where there is an dipole, the two forces applied to each charge of the dipole are equal and opposite and so the total force is zero.
From Theory
b)
The meter of the dipole torque p is:
The direction of p is of course "negative" and goes from the '-' pole to the '+' pole with an angle of 180 - 35 = 145 degrees (clockwise) to the electric field.
c)
The meter of the torque is:
Torque is the dot-product and so goes to the "third-dimension"
Using the right hand rule we know that the torque points outwards of the "page".
(will get into that in Classical mechanics later on...)
d)
Using the equation for potential energy we covered last time we get:
Of course the potential energy is positive, cause the angle is greater then π/2 and smaller then π.
Nothing special about this example actually. Just applying formulas :P
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
And this is actually it for today!
Next time we will start getting into Electric flux and Gauss's law!
Bye!
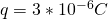
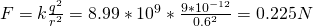
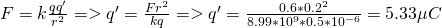
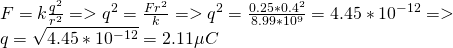
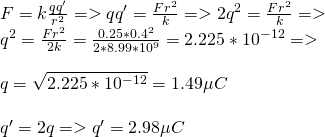
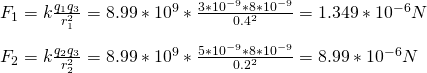
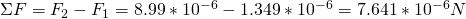
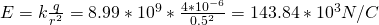
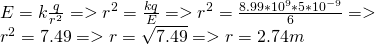
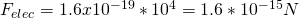
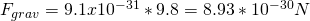
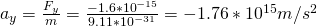
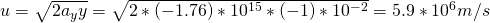
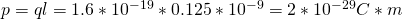
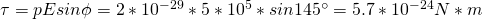
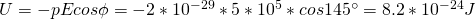
Well done, thank you
I'm glad that you enjoyed it!
Took some effort to make :)
Dear @drifter1:
I apologize for getting 2 comments by @steemstem-bot on your post. The reason it was caused (when looking at the log file written) is that it sent the comment and received a 500 error code so it tried to send it again however both comments must have been received by the nodes. It happens to relatively few people compared to all the comments made. The other problem is that the other failsafe, which checks the most recent block for a comment made by the account on that post, only checks 1 block so if the comment is put in 1 block later then my failsafe won't work. Again, my apologies.
Sincerely,
Kryzsec
Physics my best subject ever
Being A SteemStem Member
Being A SteemStem Member