Physics - Electromagnetism - Electric fields and field lines
Introduction
Hello it's a me again Drifter Programming!
After covering Coulomb's law we can now proceed with Electromagnetism by talking about Electric fields! Electric fields and field lines are very important and so this post will contain a lot of knowledge :)
So, without further do, let's get started!
Electric fields
We know how to calculate the electic force applied from one or more charges to another, but
- How does a charge know that another charge is there?
- What is between those charges?
Those questions can be answered if we restate Coulomb's law.
The same way as we have Gravitational fields that explain how gravity keeps us on top of the planet (will get into that some day in another branch xD), we also define Electric fields.
Gravity only pulls object, whilst electric force can push or pull depending on the signs of the charges.
To define electric fields let's talk about the repel force between two positive charges.
In the picture, we have two charges Q and q.
Q applies a force F to q that we can calculate using Coulomb's law as we said in my previous post.
Let's now think about Q as an object that gives the environment around it some properties.
Let's also remove q and replace it with a point P with no charge that describes any point around the charge Q.
We say that Q produces or causes an electric field at the point P.
That way if we place any test charge q' at P then the electric field will apply a force F' to it.
(Of course q or q' also create an electric field that applies a force to Q)
So, whenever we want to check if there is an electric field somewhere (in an experiment), we just put an test charge and see if an electric force gets applied to it or not.
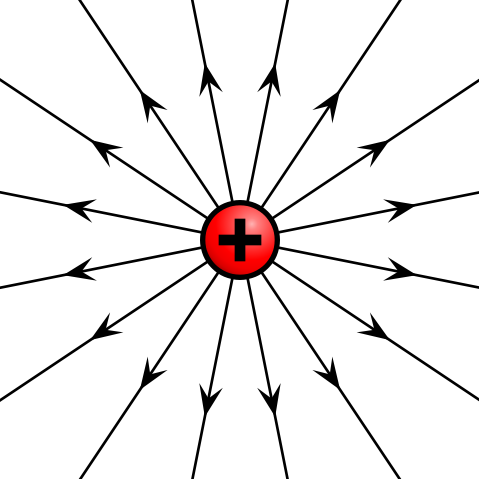
An electric field looks like this:
Of course the lines show the direction of electric force applied to a positive charge q.
A negative charge would get an opposite (but equal in value) force applied.
Electric force is an vector unit and so does the electric field.
We calculate electric fields in N/C (or V/m as we will see later on) in the SI system.
So, if E is an electric field and q' a test charge which has gets force F' applied by E then:
Of course q' can be negative or positive:
- If positive then E and F' have the same direction
- If negative then E and F' have the opposite direction
After all this we can understand that an electric field is an vector field which contains an infinite number of vectors, where each one of them corresponds to an specific point in space.
There is still a slight problem tho.
If q' is almost not charged (~0 charge) then we need to get the limit of the previous formula:
There is also another problem which has to do with the source of the electric field.
If the source is an conductor of electricity then the electric field's distribution will change.
In Electrostatics (where the charges don't move) we say that:
The electric field of each point inside of a conductor must be zero.
The value (meter) and direction can differ a little because of the electric field's source material, but if they don't then we say that the field is uniform.
Using the formula we talked of earlier and Coulomb's law, we can now find another equation that gives us the electric field E that starts from a source point S and gets applied to a point charge q at P, using an unit vector r as:
Mostly, we just need the value/meter tho.
By definition the electric field applied to a point charge "leaves" from a positive charge and "gets into" a negative charge.
So, to sum up:
A given charge distribution acts as a source of an electric field and applies an electric force to any charge that gets into this field.
Solving problems around Electric fields
We talked about how we calculate the electric field from a charge distribution that comes from a single source point.
When having more we use the same superposition principle as last time and so we calculate the electric fields E1, E2, E3, ... that are being produced by the point charges Q1, Q2, Q3, ... and then find the vector addition of them.
So, the total electric field E at some point P will be:
These are some more terms that are very useful:
- When the charge is distributed along a line than we are talking about linear charge density (calculated in N/m)
- When the charge is distributed along an area then we talk about area charge density (calculated in N/m^2)
- When the charge is distributed in 3-dimensional space then we talk about volume charge density (Calculated in N/m^3)
Those densities will sometimes even need Integrals to be calculated!
Either way, here some tips:
- Use the right metrics! Distances in meters, charges in Coulomb's
- To calculate vector sums we mostly use component vectors.
- Distinguish the vector and scalar units!
- To find the direction of the electric field E always discern the source point S and point P of the field.
- The electric field caused by an positive charge goes to the point P, whilst the electric field caused be an negative charge goes from P to S.
- When having more advanced distributions of charge, we find small elemental points of charge that can be considered electric field sources on their own. After that we calculate each field produced and find the sum. So, always find each component electric field on it's own.
- Be sure that you don't calculate each charge twice, when in an symmetrical distribution.
We will get into examples after covering Dipoles :)
Electric field lines
Let's finally also talk about the force lines that electric fields are represented with.
The whole definition of an electric field is abstract, but force lines make it easier for us to understand them and make those electric fields more "real".
An electric field line is an imaginary line drawn in an area of space, so that at every point of this line the vector of the electric field is tangent to this point.
So, those electric field lines show us the direction of an electric field E at each point.
The electric field lines also give us an idea of the "size" of the electric field E.
When E is strong then we make the lines densely and when E is weak then we make them sparsely.
One important property of them is that they don't intersect. At each point the electric field has one and only direction, and so only one electric field line passes from a point in space.
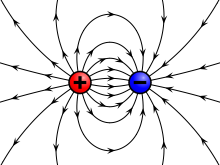
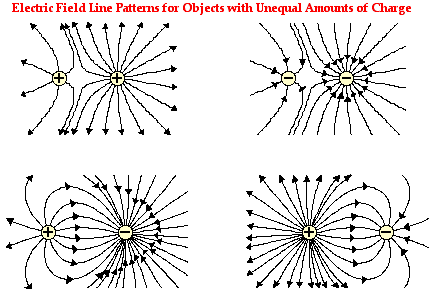
Here some so called electric field representations:
Those electric fields have unequal amount of charge and different signs so that you see the difference I was talking about earlier.
- In the first two fields we have two positive and two negative charges, but the right one's electric field is more dense which means that the right one has a greater value of charge.
- Below are two examples with opposite signs, where in the first one the negative charge is stronger, whilst on the second one the positive charge is stronger!
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
And this is actually it and I hope that you enjoyed it!
Next time we will get into Electric dipoles!
Bye!

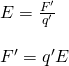
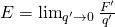
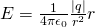
Good post. Great topic as electromagnetism is present in our everyday lives.
thank you for the simple explanation to electric fields and electric lines of forces. Am I ready for Maxwell equation now? :P
Nope :P
@resteemator is a new bot casting votes for its followers. Follow @resteemator and vote this comment to increase your chance to be voted in the future!