Physics - Electromagnetism - Electric capacitance exercises
Thumbnail build using: Capacitor diagram
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into examples/exercises all around Capacitors and Capacitance that we covered during the last 4 posts!
I highly suggest you to read these 4 posts of Electromagnetism from Capacitance up to Dielectrics, cause this post will simply be an mathematical application of the topics that we discussed there...
All the mathematical equations will be drawn using quicklatex!
So, without further do, let's get straight into it!
To make it smoother for you I will start with simple capacitor calculations, continue on with combinations, electrical energy and density, and lastly dielectrics (actually exactly the order in which we did the posts!).
Capacitor calculations
Suppose we have a capacitor build up of 2 parallel conductive metal plates (like the one that we covered through-out this series) and that there is nothing in between of those plates.
The capacitor has:
- a capacitance C = 500pF
- charge Q = 0.2μC on each capacitor plate and
- the plates are d = 0.4mm apart.
Calculate:
- The potential difference (V) between the capacitor plates
- The area (A) of each capacitor plate
- The electric field magnitude (E) between the capacitor plates
- The surface density of charge on each capacitor plate
The capacitance (C) of such a capacitor can be calculated using:
or using the more general equation:
1.
Using the general equation we can calculate the potential difference like that:
2.
Using the other equation we have:
3.
When having parallel plates (and so capacitors) we proved that the electric field and voltage are binded by the equation:
We know the potential difference (V) and the distance (d) and so can calculate the electric field like that:
4.
For the last bit we simply have to divide the charge (Q) with the area (A) which gives us:
In other examples we might know the voltage, area, electric field or charge density and might need to find the capacitance, charge or distance of the capacitor! Either way these are the "needed" equations for simple capacitors!
Capacitor combinations
During the post about capacitor combinations and problems we solved a "simple" example, where we only had to calculate the total/equivalent capacitance of the combination. But, I also told you that the potential and charge might also be asked in some examples and so here we go!
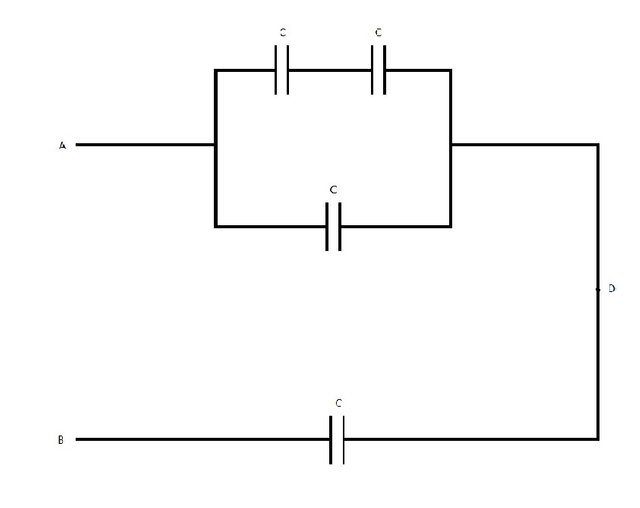
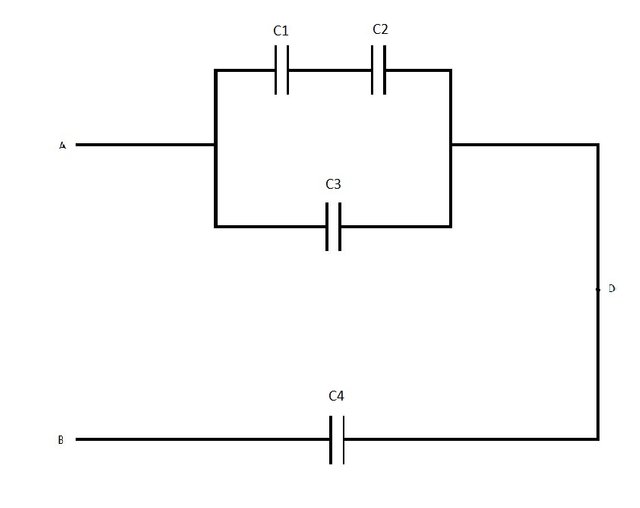
Suppose we have the following capacitor diagram:
where:
- all capacitors have the same capacitance C = 2μF.
- the potential difference of A->B is Vab = +36V
Calculate:
- The charge (Q) of each capacitor
- The potential difference (Vi) between the plates of each capacitor
- The potential difference between the points A and D (Vad)
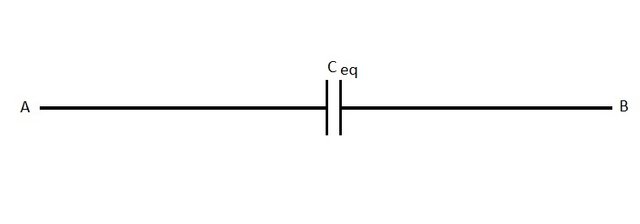
Let's first calculate the total/equivalent capacitance step by step...
First we combine the two serial capacitors:
which give us a capacitance:
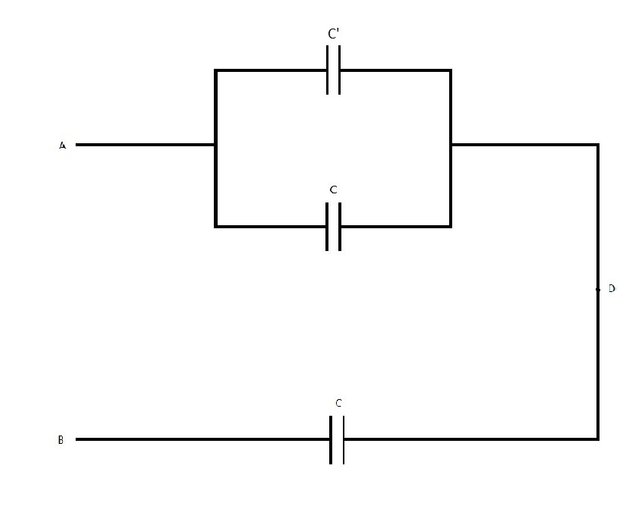
Next up is the parallel combination of C and C' which gives us:
and a capacitance:
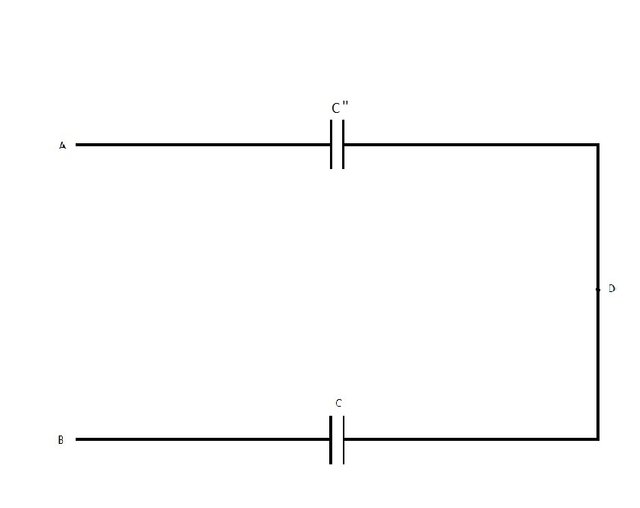
Lastly we combine C'' and C that a serially connected and get:
which gives us the total capacitance:
We might want to give "names" to the capacitors like that:
Side-note: All these diagrams are made by myself!
So, let's now get into the actual exercise "questions"...
We build up back to the original circuit...
From the last diagram we can calculate the total charge which is:
The capacitors C4 and C" in the third diagram are in a serial connection and so have the same charge, which means that the charge of C4 is equal to Q4 = 43.2μC.
The potential difference of C4 is:
When in a serial connection the potential differences add up to the total which means that:
Which of course is the potential difference A->D that we are asked to calculate in 3.
Next up we go back to the second diagram where we have C' and C3 in a parallel connection. Having them in a parallel connection means that they have the same potential, but not the same charge and so using the potential difference Vad that we calculated moments ago we can calculate the charge of each capacitor now!
So, like I said V3 = 14.4V and the charge of it is:
For the equivalent we have a total charge of:
Continuing on we get to the "given" diagram where C1 and C2 are in a serial connection and so have the same charge Q = Q1 = Q2 = 14.4 μC and V' = V1 + V2. Because they have the same capacitance and charge they also have the same potential difference (which is the half of V') and so:
So, to sum up we have:
- Q1 = Q2 = 14.4μC, V1 = V2 = 7.2V (serial connection of equal capacity)
- Q3 = 28.8μC, V3 = 14.4V (equal to Vad)
- Q4 = 43.2μC, V4 = 21.6V
You use this exact procedure for any combination of capacitors!
Electrical energy and density
Examples in this category are applications of the equations we talked about in my post and so I will just get into representative examples of such problems.
1.
Suppose we have a capacitor (from the ones that we covered) with:
- capacitance C = 8μF
- distance d = 4mm between the plates
- potential difference V = 400V
Calculate the energy density (u) in the space between it's plates.
Energy density is calculated using:
Because we have this "simple" capacitor we can calculate the electric field E using:
and so:
2.
As a sub-question of other problems we might have:
What is the electric potential energy (or internal energy) stored in a capacitor C with capacitance C = 300μF and potential difference V = 240V?
We simply check what is given to us and use the correct equation of the following:
Of course C and V are known and so we use the "middle" one which gives us:
You might get this asked in other ways like this for example:
How much energy is consumed if the capacitor gets totally discharged when connecting it to a conductive cable, supposing that all his energy is turned into thermal energy.
Dielectrics
Let's get into some examples where we have to calculate one of the "elements" of a capacitor that contains a dielectric material.
1.
Let's suppose we have a capacitor (from the parallel plate ones) which has an dielectric material of dielectric constant K = 3.4 and dielectric strength 2 x 10^7 V/m. The capacitor needs to have a capacitance of C = 1.5nF and should withstand a total of 6000V of potential.
What is the minimum area (A) that each capacitor plate should have?
For such a capacitor we can use the equation:
You can see that d and A are unknown and so what now?
Well, with minimum A we mean smallest possible d, where d is of course limited by the dielectric strength.
Using E = V/d we can calculate this distance:
That way the Area is now the only unknown variable and can be calculated with ease...
2.
Suppose a capacitor where when there is no dielectric material the electric field is:
When having a dielectric material throughout the "empty" space then the electric field is:
Calculate:
- The surface density of charge in the dielectric material
- The dielectric constant (K)
The questions can be done in the opposite order!
2)
We said that the factor in which the electric field decreases when insterting a dielectric material is equal to the dielectric constant K.
And so:
1)
Last time we talked about the relation between the charge density of the plates and the dielectric material and got the equation:
The charge density at first is given by:
and so we finally have a charge density in the dielectric which is:
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
And this is actually it for today and I hope that you enjoyed it!
Next time we will start talking about electric currents!
Bye!

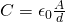
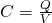
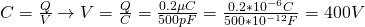
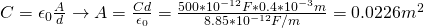
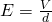
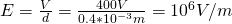
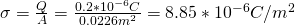
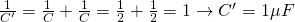
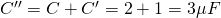
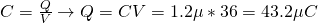
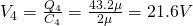
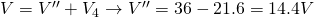
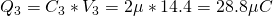
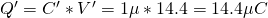
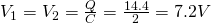
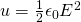
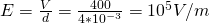
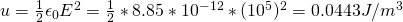
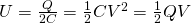
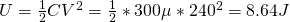
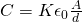
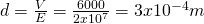
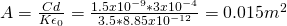
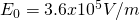
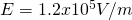
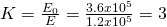
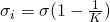
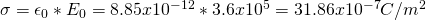
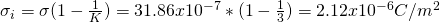
Applying all these equations is really easy and the basic theory knowledge needed to apply them is actually also not very difficult to learn!
I think that the exercises that I did are enough, but if you think that I should do some more advanced ones let me know!
Of course Capacitance will not be gone now and will be used in later posts again...the same way as we used charges, electric fields and potential with capacitors!
Read my profile if want me to resteem your post to over 72,500 followers. @a-0-0
👍