Physics - Electromagnetism - Dielectric materials
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into Dielectric materials that are placed in-between of the two conductive plates of capacitors!
All the mathematical equations will be drawn using quicklatex!
So, without further do, let's get straight into it!
Quick Recap
Till' now we supposed that the space between the two parallel conductive plates of a capacitor is a vacuum and so doesn't contain anything!
Last time we even found an equation that gives us the energy density u and this equation contained the (dielectric) permittivity of vacuum (ε0) which was:
I mentioned that this equation will be true for any conductor...
So, what exactly do we put in-between of the two plates of a capacitor?
Dielectrics
The materials in-between of those plates are called Dielectrics.
Dielectrics are non-conductive materials and so insulators of electricity.
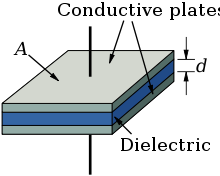
A common type of capacitor is build up of long stripes of metal sheets that are separated by plastic stripes (for example Mylar). Such a capacitor is very small, but has a "large" capacity of some μF and so is very useful for a lot applications!
Here you can see how such capacitors are basically build up:
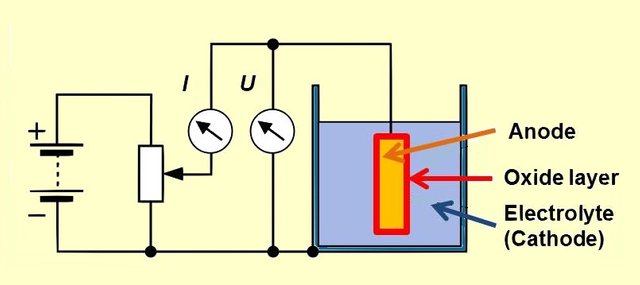
Electrolytic capacitors are also a very interesting type of capacitor!
They use a very thin layer of insulative oxide in between of a metal plate and a conductive solution.
We know that the capacitance C is inverse proportional to the distance d between the plates of a capacitor, because:
Because of that electrolytic capacitors of relatively small size have a capacitance of 100 up to 1000μF!
Here you can see the basic principle of such capacitors:
There are basically 3 reasons for which we need and use dielectrics:
- They solve the mechanical problem of restraining large metal plates in place with a very small distance in-between of them so that they don't contact. We basically separate them using such materials.
- Dielectric materials "suffer" of Dielectric (or Electrical) Breakdown, which means that they become electrically conductive after the current that flows through them exceeds their breakdown voltage. They basically become conductors of electricity and can even withstand stronger electric fields. Each dielectric material has a dielectric strength (We will get back to this later on).
- The capacitance of a capacitor is larger when there is a dielectric material, when comparing it to air or vacuum.
Let's now get into the properties of Dielectrics...
Dielectric constant (relative permittivity)
Let's say that the initial capacitance of a capacitor is given by:
and that the capacitance when having a dielectric material is:
The charge Q in both cases is of course the same, but the "new" voltage V is smaller then the initial voltage V0, cause as told before the "new" capacitance C is of course greater then the initial capacitance C0.
The ratio C by C0 (equal to V0 by V) is defined as the dielectric constant or relative permittivity of a dielectric material and is noted as K (or εr):
We can get into the conclusions:
- the capacitance is increasing by factor K, while potential is decreasing by factor K.
- K is a "clear" number greater then 1, cause C is always greater than or equal to C0.
- Of course K = 1 for a vacuum.
Dielectric permittivity
Let's say we want to decrease an electric field E0 by factor K then the new electric field E will of course be:
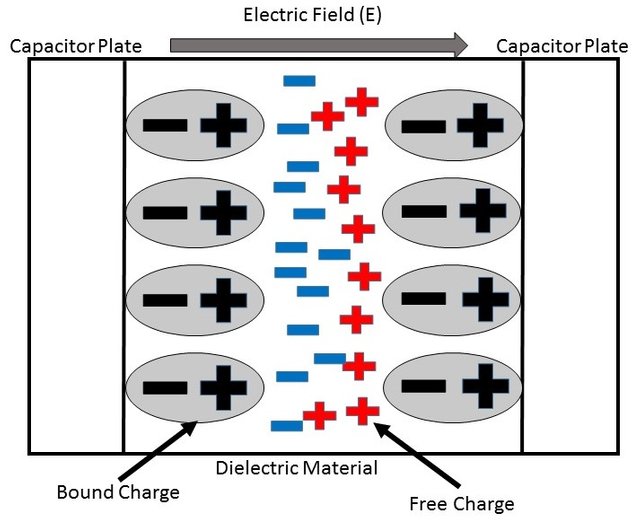
This means that a dielectric material decreases the electric field or decreases the energy density of charge. Of course the surface charge density of the conductors doesn't change, but opposite charge inducts on each side/surface of the dielectric material. These inductive charges are caused by the reallocation of charge inside of the dielectric material, something called polarization!
The inductive charge is of mostly proportional to the electric field E inside of the dielectric material, where the dielectric constant K is characteristic for each material. When having very strong electric fields or unstable materials then things change, but let's only talk about the "simple case".
Let's find a relation between the inductive charge and charge on the surface of the plates.
Let's represent the surface charge density as σ for the capacitor and σi for the dielectric material specifically. The total surface charge density on each plate of the capacitor is: (σ - σi).
The electric field E between the plates is calculated using the total surface density and so:
When having a dielectric material this becomes:
Using those equations we end up with an equation that calculates the inductive charge density σi using the total charge density σ and dielectric constant K, which is:
This equation shows us that if K is very big than σi is almost as big as the total charge density σ! In such a case the density σi cancels out the total charge density σ and so the electric field and potential difference become a lot smaller then the values that we have in a vacuum!
The product k*ε0 is called permittivity of the dielectric material and is represented by ε.
Using the permittivity ε the electric field E now is:
And the capacitance when having a dielectric material is given by:
When in a vacuum then K = 1 and so ε = ε0. The value ε0 is called vacuum permittivity or electric constant!
Redoing the prove of last time we can now end up with the energy density u when having dielectrics which is:
And so supposing that the charge of each plate stays the same, the value of εo gets multiplied by the factor K, which means that the electric field E decreases by factor 1/K and so does the energy density u. The remaining energy goes to the "outer" electric field that we previously never took into our calculations. We will not need this in our "simple" examples, but either way it's interesting to know what happens!
Dielectric strength
We previously said that any dielectric material that a strong electric field is applied to becomes conductive and we called this phenomenon Dielectric Breakdown.
The maximum electric field or voltage that a material can withstand defines the dielectric strength of it. This means that the material "breaks appart" after getting such a strong field applied.
This value is strongly dependent of:
- temperature
- mixture "scents"
- small anomalies
- metal electrodes
- and more...
This means that we can only give approximate values to the dielectric strength of materials!
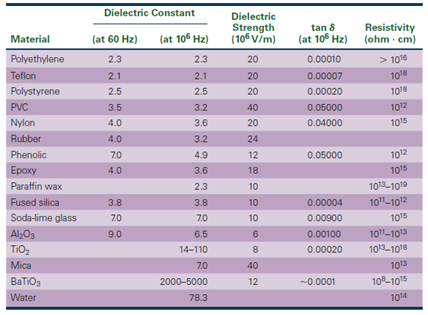
Here a table of some dielectric strengths and constants of common materials:
How to solve problems around Dielectrics
Solving problems that contain dielectrics is not very difficult.
Here some tips:
1) Always use the correct metrics (like I say every time):
- meters (m) for distances (they will never be directly meters, but mostly cm)
- N/C or V/m for electric field magnitude (whatever is easier)
- C^2/N*m^2 or F/m for permittivity (ε0 mainly)
2) There is a flood of equations that apply to Electromagnetism:
- always ask yourself what each symbol represents.
- learn to distinguish charges and charge densities and also electric fields and potentials.
- remember that the capacitance of a capacitor with dielectrics is greater then the one without a dielectric material.
- the inductive charge density σi in the dielectric material is always smaller then the charge density σ of the plates of the capacitor.
- When the charge Q of the plates is given then the electric field and potential difference decrease in the presence of a dielectric material when compared to the absence.
Examples/Exercises next time!
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
REFERENCES:
- Dielectric: https://www.britannica.com/science/dielectric
- Electrolytic capacitor: https://en.wikipedia.org/wiki/Electrolytic_capacitor
- Electrical Breakdown: https://en.wikipedia.org/wiki/Electrical_breakdown
- Relative permittivity: https://en.wikipedia.org/wiki/Relative_permittivity
- Vacuum permittivity: https://en.wikipedia.org/wiki/Vacuum_permittivity
- Dielectric strength: https://www.elandcables.com/the-cable-lab/faqs/faq-what-is-dielectric-strength
And this is actually it for today and I hope that you enjoyed it!
Be happy, cause next time we will get into exercises around capacitors!
Bye!
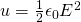
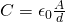
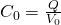
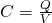
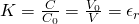
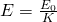
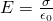
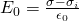
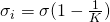
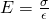
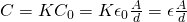
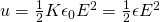
Nice work you are doing here @drifter1 .. You'll make a great physics tutor
Hi @drifter1!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV