Physics - Electromagnetism - Electric potential energy
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into Electric potential energy!
A lot is based on Work and Energy of Classical Mechanics that I didn't do yet there, but I will cover any part needed for sure!
So, without further do, let's dive straight into it!
Quick explanation of Work and Energy
When a Force F acts on an object that moves from a point a to a point b, then the Work W that is produced by that Force is:
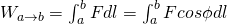
where dl are small distances along the trajectory of the object and φ is the angle between F and dl at each point of the trajectory.
Work and Energy are calculated in Joule's (J).
When the Forces of a Force-Field are conservative then the Work can always be expressed using some potential energy U.
So, when the potential energy is Ua at some point and Ub at some other point then:
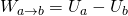
The Work is positive when Ua is greater then Ub, which means that the potential energy decreases.
Always remember that the Force produces positive Work when the potential energy decreases!
A nice example of Classical mechanics is throwing a ball:
- When the ball is going down then gravity produces a positive work, while the potential energy decreases!
- When the ball is thrown vertically upwards then the work of gravity is negative and the potential energy increases!
The work-energy theorem tells us that the change of kinetic energy (Ka - Kb) is equal to the total work applied to an object.
The total energy at any point is constistent and so:
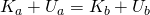
where K is the kinetic energy and U the potential energy at points a and b.
Let's get all that into Electromagnetism now!
Getting into Electric Potential energy
Suppose we have two parallel oppositely charged metal plates (+ on top) that produce an uniform electric field E. The electric field of course applies a force F downwards to any positive test charge q', whenever it moves a distance d from a point A to a point B.
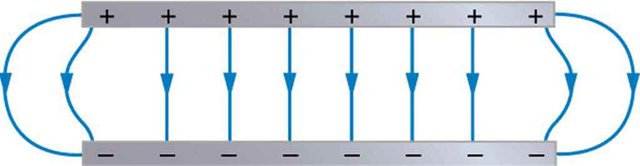
The force is of course independent of the location of the test charge and also consistent and so the Work produced by the electric field E is:
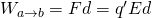
This Work can also be expressed using a potential energy U.
The y-component of the electric force is Fy = -q'E and consistent and there also are no x and z components. This means that the Work produced is independent of the trajectory that the charge takes from a point a to a point b, but only depends on the start and endpoint.
The same way as potential energy of gravity Fy = -mg is U = mgy, the potential energy of the force of an electric field Fy = -q'E is:
U = q'Ey
And so when a test charge moves from a height ya to a height yb, the Work produced on that charge from the field is given by:
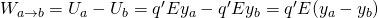
When the height ya is greater then yb then the charge moves in the direction of the electric field E, the potential energy U is drecreasing and the Electric field produces a positive Work.
In the same way, when ya is smaller then yb then the charges moves oppositely to E, the potential energy U increases and the field produces a negative Work.
More specifically if we set ya = d and yb = 0 then:
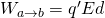
Until now we only had a positive charge...
What's true for negative charges?
When a test charge q' is negative then the force applied goes in the opposite direction of the field and so:
- The potential energy increases when the charge moves in the direction of the field and decreases when the charge goes in the opposite direction.
- The work of the field is negative when the charge moves in the direction of the field and positive when the charge moves in the opposite direction (and so the direction of the force applied to it!)
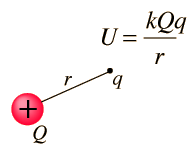
Electric Potential Energy
Let's now generalize it and talk about the Work that is produced on a test charge q', when it moves in the electric field of a static point charge q.
Let's first get into a trajectory along the radial line from a point a to b.
The radial component of the force using Coulomb's law is of course:
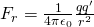
When q and q' are oppositely charged then the Force is negative (attract) and when the charge have the same sign then the force is positive (repel).
The force is not the same at a and b, because the distance r changes and so we need integration!
The Work that is produced to q' from the force Fr (that is applied by a charge q), while q' moves from a point a to a point b is:
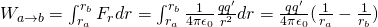
We can clearly see that the Work at that trajectory depends only on the start and end points!
In reality, the work is the same for any possible trajectory from point a to b.
Proof?
Let's suppose two points a and b that are not on the same radial line.
The Work produced to q' along such a trajectory is given by:
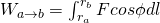
By making a schema we would see that cosφ dl = dr. I don't found a good one... :(
Anyway, that means that the work produces at a small displacement dl depends only on the change dr of the radial distance (and so component) r between the charges.
And so, the Work produced to q' from the field E that is generated by q is independent of the trajectory and only depends on ra and rb, which are the radial distances of the start and end points!
Something interesting is that if we make a cycle and start from a point A and go to the same point A, in the end the work produced is zero!
Of course all this works only if the force-field is conservative, something that is true for electromagnetic forces!
So, by using the equations we covered 'till now we can now say that the potential energy when moving along a distance r is:
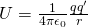
Which of course is true for any charge q' and q!
We could also use a spherical uniform distribution of charge instead of a point charge q that produces an electric field, as we already know from Gauss's law, cause such a distribution works like it has all the charge concentrated in the center!
The potential energy depends the point of reference, where we have U = 0.
U = 0 when the distance between the charges q and q' is infinite, r = ∞.
One last thing is...what do we do when there are more charges?
Well, we again use the superposition principle...
Which means that the potential energy of a test charge q' at distances r1, r2, r3, ... away of some charges q1, q2, q3, ... is the algebraic (not vector!) sum:
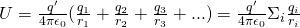
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
And this is actually it for today and I hope that you learned something!
Next time we will continue on with how we calculate electric potentials!
Bye!
I really love and appreciate your vivid use of mathematical equations and physical relationships in explaining this subject. Being an engineer myself, I understand the importance of scientific and mathematical harmony when it comes to the field of physics, chemistry or even biology. Thanks for your explanations too!
Thank you!
I try to make the math behind physics seem simpler then it actually is. Of course sometimes complex math cannot be avoided, but still giving a good "theory" explanation of what we are talking about helps anyone understand!
Glad that you enjoyed it :)
Very true indeed! I couldn't agree more :)