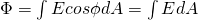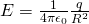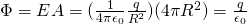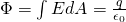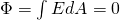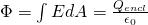Physics - Electromagnetism - Electric flux and Gauss's law
Introduction
Hello it's a me again Drifter Programming!
Today's topic of Physics in the branch of Electromagnetism is Electric flux and Gauss's law! I will first get into what we call Electric flux and then will give some information about Gauss's law, a law that we will cover in-depth next time :)
So, without further do, let's dive straight into it!
Getting into Gauss's law
Gauss's and Coulomb's law are two alternatives that define the correlation between a distribution of charge and the electric field it generates.
Coulomb's law of course defines the electric field at a point P generated from a point charge q. When having an extensive distribution of charge we suppose that this distribution is build up of many point charges using the Superposition principle and so "adding" all those field's together.
Using Gauss's law on the other hand (that we will cover in today's and the following two posts) we assume that an charge distribution is surrounded by a hypothetical surface. That way we only have to find the electric field at points on top of that surface. Gauss's law is a correlation between all the points of that surface and the total charge that is surrounded by that surface.
Electric flux
To define Gauss's law we first have to define the concept of Electric flux.
The definition of Electric flux contains the area A of a surface and an electric field E that is applied on the points of the surface.
This surface of course doesn't have to be real! It's an imaginery surface in space!
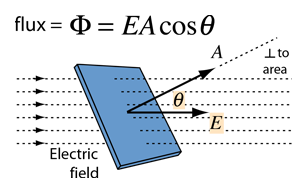
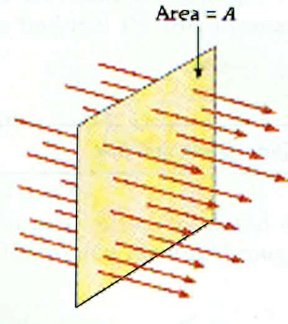
Let's consider a small, flat surface of area A vertically across to an uniform electric field E:
We define that the electric flux Φ that passes through the surface A is equal to:
Φ = EA
and so the product of the area and electric field.
We can represent Φ roughly through the elecric field lines of E that pass through A.
- A larger area A means more lines pass through
- A stronger electric field => denser electric field lines
And so when these two things are true we have more lines/surface-unit.
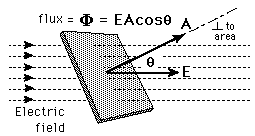
But, what if the surface is not vertically across to the electric field?
Of course less electric field lines pass through the surface.
So, of importance is the projection of A to an hypothetical vertically across surface to E.
When having an angle θ, the Electric Flux Φ is:
Φ = EAcosθ
where Ecosθ is the component of E that is vertically across to the surface A.
This looks like this:
To make the definition even smaller and to make it more general we determine the concept of a vector area A, which is a vector unit with meter the area A of a surface and a direction vertically across to the surface we are describing.
The vector area A now defines the meter of the area and also the orientation in space.
The "new" equation is:
Φ = EA
where all variables are now vectors.
All those equations express the concept of Electric Flux in a different, but equivalent way!
By using any of those definions we have that Electric Flux is calculated in Nm^2/C in the SI metrics system.
So, what remains now?
Well, we covered the "simple" electric flux that is applied to a small, vertical (or with angle θ) surface A from an uniform electric field E.
What if the electric field is non-uniform and what if the surface is part of a curved surface?
Here we go again...integrals
We of course split the curved surface into small elementary dA areas and calculate the electric flux that passes through each of them.
That way Electric Flux is calculated through:
where in the first E, dA are scalar units, while in the second E, A are vector units.
Such an integral is of course a surface integral, like those that we covered in Mathematical analysis...
A lot of times we represent the direction of an elementary surface A using an unit vector n that is vertically across to that surface.
That way:
dA = ndA
where the A on the left is a vector and the A on the right is a scalar unit.
The vertically across vector n can go to any direction and so we have to choose between the "inside or outside" surface.
We always choose the direction of n that goes to the outside space of the surface and so talk about an Flux that goes outwards.
Gauss's law
So, what is Gauss's law?
Gauss's law states that the total electric flux that goes through any closed surface (with some volume) is proportional to the total charge that this surface contains.
Let's start with an positive point charge q and it's electric field.
The electric field lines stretch outwards to all the directions radially around and so by placing the charge in the center of an imaginary sphere surface of radius R the meter of the electric field E at any point on that sphere is:
At every point of that surface, the electric field E is vertically across to the surface and the meter is also equal, because the distance is the same.
That way the total electric flux is simply the product of the electric field's meter and the total area of the sphere which of course if A = 4πR^2 and so:
We can clearly see that:
The electric flux is independent of the radius R of the sphere and only depends on the charge that sphere surrounds.
Using that we can say that:
What applies to the whole sphere also applies to a part of it!
When having an non-sphere surface we just have to split it up into small elementary "spheres" of dA area which means that the total flux will of course be the surface integral:
This equation is true for any surface that surrounds the charge q and is closed!
The elementary areas dA and their corresponding unit vectors n of course "tend" outwards and so the electric flux is positive at points where the electric field lines go outside of the surface and negative when they direct inside. Of course the opposite applies for negative source charges!
For any closed surface that doesn't contain charges we have:
This is the mathematical equation that shows us that a surface doesn't contain charges or has the same amount of charges entering and leaving the surface! So, the electric field lines can start or end at a specific space area only when there is a charge at that area.
One last thing remains now...
What about more charges that are being closed of the same (sphere or non-sphere) surface?
Let's suppose those are q1, q2, q3, ..., gn.
The total electric field is of course equal to the vector sum of the electric field's generated by each one of those charges if we look at them individually.
Let's also define the total enclosed charge as Qencl = q1 + q2 + ... + qn.
By also defining elementary areas dA and the vertically across components of the total electric field E to that areas, we then define the general Gauss law:
When Qencl = 0 then the total flux that passes through the surface must also be zero, even when some areas have positive or negative flux.
All these different equations that we showed for Gauss's law define the same thing, but with different sizes an so we will choose one instead of the other depending on the problem we have to solve.
We will get into Applications next time...
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
And this is actually it for today and I hope that you enjoyed it!
Next time we will get into Applications of Gauss's law
Bye!