Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 4

Let's work through another example on how to solve non-homogeneous 2nd order differential equations. This is our final example before we look at practical applications of this method of solving ODE's. This example has yet another subtle twist from the previous 3.

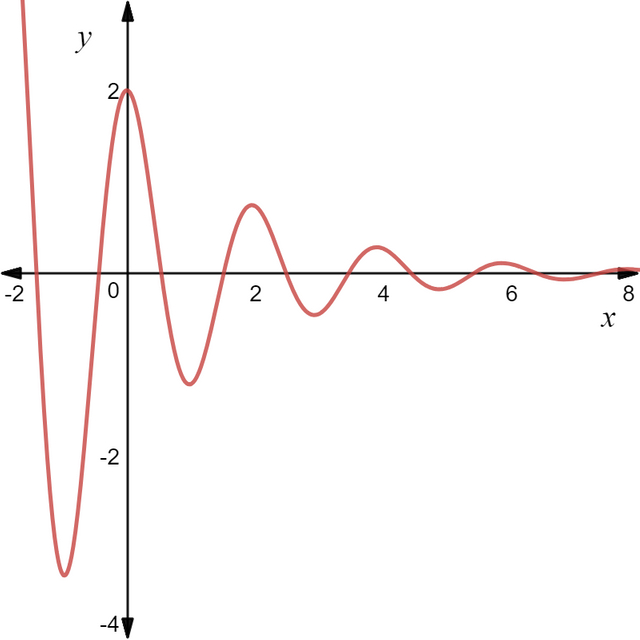
Figure 1. Graph of the particular solution to equation (1) in Example 4.

So without further adieu, let's work through Example 4.

Example 4

Let's find the particular solution to...

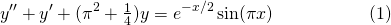
...with initial conditions:

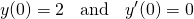
The first step,as usual, is to solve for the homogeneous equation...

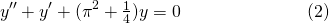
The characteristic equation for (2) is...

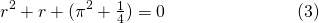
The roots of characteristic equation (3) are...

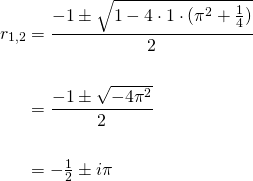
So we have complex conjugate roots. Thus by equation (11) of post #3, the homogeneous solution is...

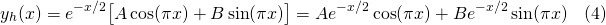
Now, for the particular solution of the non-homogeneous equation, let's see what happens when we try:

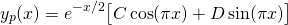
(note: this trial for y_p is in exactly the same form as y_h, and as you'll soon see, we are going to run into problems)

The first and second derivatives for y_p are...

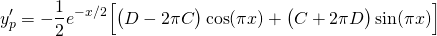
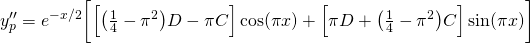
Sub these into (1) and we get...

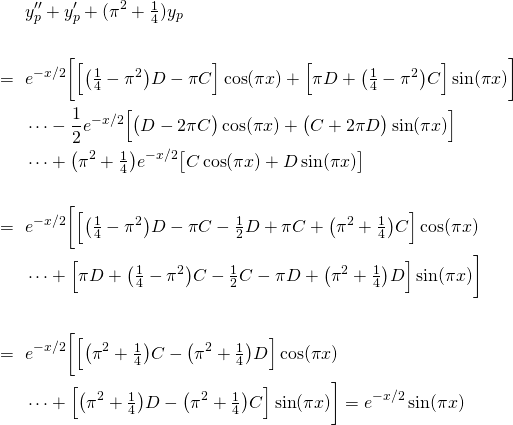
Now equating the coefficients of the left hand side to the right hand side...

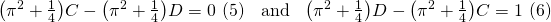
Do the simultaneous equations (5) and (6) make sense? From (5)...

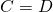
...which means by (6)...

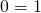
...an impossible result!

So how did this happen, and how do we solve it? Basically, this is the same situation as Case II in post #3, in that we need y_p and y_h to be linearly independent to form a basis for the particular solution.

See how expensive in effort math can get? Sigh...

So how do we work around that? Let's 'Modify' the trial solution a little bit by multiplying by x. Let's try...

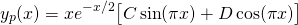
...and therefore...

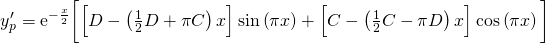
...and...

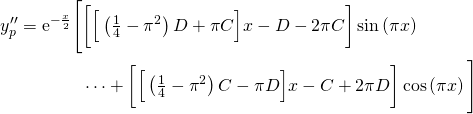
Substituting these into (1), we get...

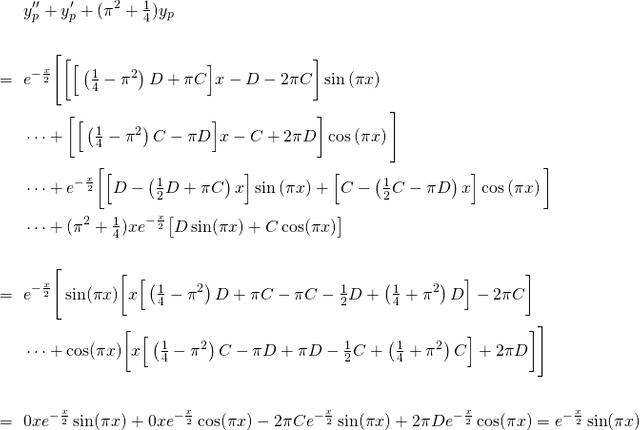
Again, by equating coefficients, we have...

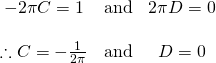
Therefore we have found a solution for y_p!

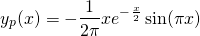
The general solution of (1) is the addition of the homogeneous solution and the particular non-homogeneous solution...

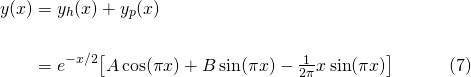
To find the particular solution to (1), we need to apply the initial conditions. Firstly,

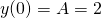
The first derivative of the general solution is...

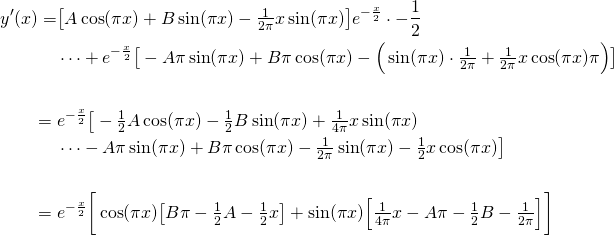
And applying the second initial condition...

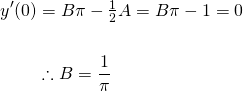
Finally...

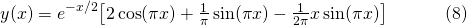
Figure 1 above is a graph of the solution, equation (8). This tutorial was an example of using the "Modification" rule whereby if the choice for y_p is a solution in y_h, we need to modify the choice by multiplying by x, or x².

Summary of the Method of Undetermined Coefficients

a) Basic Rule

Table 1 below describes the choices for the particular solution to the non-homogeneous equation for the given non-zero term r(x).

Term in r(x)	Choice for yp(x)

Table 1. Basic rule, choices for y_p(x)

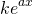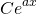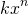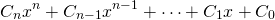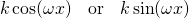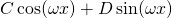b) Modification Rule

If the choice for y_p(x) is a solution of y_h(x), multiply the term by x (or x² if the solution is in the same form as a double root of the characteristic equation of the homogeneous ODE)

c) Sum Rule

If r(x) is a sum of functions in the first column of Table 1, sum the corresponding choices for y_p(x) in the second column

---

Credits:

All equations in this tutorial were created with QuickLatex

---

First Order Differential Equations

1. Introduction to Differential Equations - Part 1
2. Differential Equations: Order and Linearity
3. First-Order Differential Equations with Separable Variables - Example 1
4. Separable Differential Equations - Example 2
5. Modelling Exponential Growth of Bacteria with dy/dx = ky
6. Modelling the Decay of Nuclear Medicine with dy/dx = -ky
7. Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky
8. Mixing Salt & Water with Separable Differential Equations
9. How Newton's Law of Cooling cools your Champagne
10. The Logistic Model for Population Growth
11. Predicting World Population Growth with the Logistic Model - Part 1
12. Predicting World Population Growth with the Logistic Model - Part 2
13. What's faster? Going up or Coming Down?

First order Non-linear Differential Equations

1. There's a hole in my bucket! Let's turn it into a cool Math problem!
2. The Calculus of Hot Chocolate Pouring!
3. Foxes hunting Bunnies: Population Modelling with the Predator-Prey Equations

Second Order Differential Equations

1. Introduction to Second Order Differential Equations
2. Finding a Basis for solutions of Second Order ODE's
3. Roots of Homogeneous Second Order ODE's and the Nature their Solutions
4. Modelling with Second Order ODE's: Undamped Free Oscillations
5. Modelling Car Suspension with ODE's: Damped Free Oscillations Part 1
6. Modelling Car Suspension with ODE's: Damped Free Oscillations Part 2
7. Modelling Car Suspension with ODE's: Damped Free Oscillations Part 3
8. Non-homogeneous Differential Equations
9. Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 1
10. Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 2
11. Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 3
12. Solving Non-homogeneous ODE's: Method of Undetermined Coefficients Part 4

---

Please give me an Upvote and Resteem if you have found this tutorial helpful.

Feel free to ask me any math question by commenting below and I will try to help you in future posts.

Visit my YouTube Channel at: https://www.youtube.com/masterwumathematics

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3

Tip me at PayPal: https://paypal.me/MasterWu