Torricelli's Law. There's a hole in my bucket, and it's a cool Math problem!

Evangelista Torricelli, an Italian physicist postulated that the velocity of a fluid flowing through a sharp edged hole at the bottom of a tank or vessel filled to a certain height h would be the same as any object of falling freely from that height.

Image Source

Now we know the relationship between velocity of an object and the height that it's dropped from can be found from energy methods, or the conversion of potential energy to kinetic energy. That is...

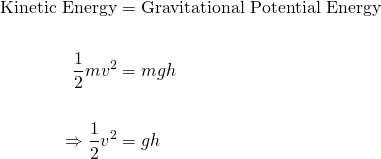
Now, this law applies to any object.

Let's assume that the object in question is simply a droplet of water amongst the entire volume of water sitting at the top of the vessel when it is filled to a height h. Now let's imagine that all of the water except this droplet is removed, so that this droplet is suspended in a vacuum at height h, and then allowed to free fall.

Torricelli's theorem suggests that the velocity of the stream of water leaking from a sharp orifice (i.e. a hole at the bottom of the tank or bucket) this the same as the free-fall velocity of this droplet of water dropped from the filled height.

And therefore, we have Torricelli's Law...

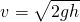
Don't worry, I had a bit of a hard time getting my head around this too, but there are experiments that can confirm this.

Now, we can use this theorem to calculate how long it takes a vessel to drain completely, because a decrease in the volume in the vessel is simply equal to the volume that leaks out of the hole.

A small volume that leaks out is equal to the velocity of the jet by the area of the hole (A₀) by a small increment in time. That is...

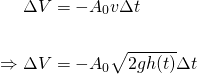
The negative sign simply means that the volume of water in the tank is decreasing.

Now, the decrease in the tank volume is also equal to the cross-sectional area (A_T) of the tank by the change in height. That is...

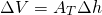
Now equating these together, we have...

By taking the limit as , we have the differential equation...

Equation (1) is a separable, first order ODE for which we can find a general solution...

Equation (2) is the general solution.

Example 1: There's a hole in my bucket!

Dear Liza, dear Henry...

For our particular case, let's assume we have a cylindrical 5 gallon bucket with diameter d_T = 30cm, and height 40cm as shown in Figure 1. Let's also suppose that at the bottom of the bucket, we've drilled a hole d₀ = 5mm and plugged it up. We fill the bucket to the brim.

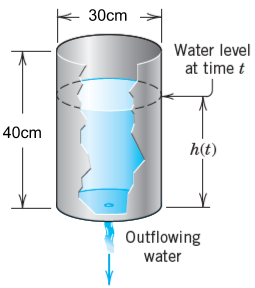
Figure 1.
Adapted from: Advanced Engineering Mathematics, Kreyszig, 10th Edition

How long does it take for the bucket to completely drain? Let's find out...

We unplug the hole at time t = 0.

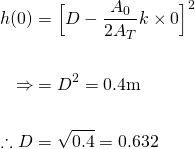
We can also find now find a numerical value to the coefficient of t (the second expression inside the brackets)...

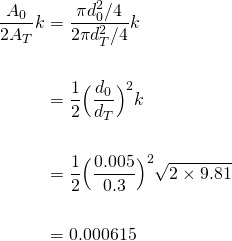
And hence the particular solution for our bucket problem is...

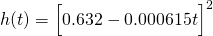
Now the bucket is completely drained when h = 0.

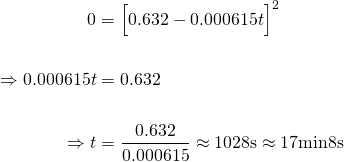
Therefore it takes just over 17 mins for this 5 gallon bucket to completely drain with a 5mm hole at the bottom.

A graph of this solution is shown in Figure 2 below...

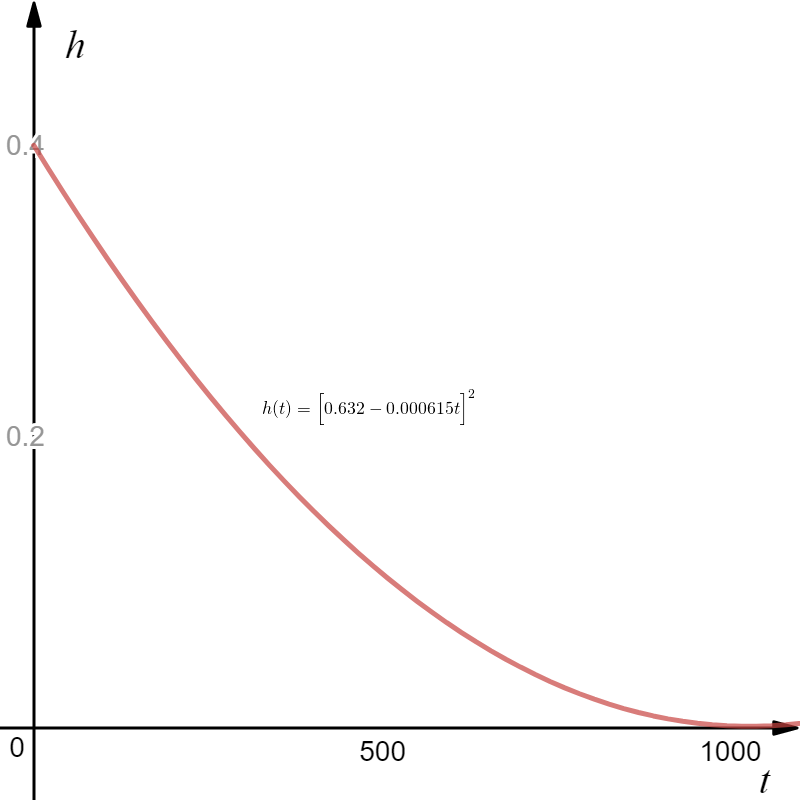
Figure 2.

Note that the curve starts to rise after a time of 1028s. This is because the analytical solution is still valid. In fact, it is valid for all real numbers of t. However, this wouldn't make sense physically because we know that in general, time cannot have a negative value and the water is not going to reverse its flow after all of it has drained from the bucket.

Ok cool. You might be thinking: "Great, I can now calculate how long it takes for a leaky bucket to empty, but who cares? What use is this?"

Well, equation (2) may come in very handy for putting out fires, as I'll explain in the next example.

Example 2: Height of Reservoir Tank required for Emergency Sprinkler System

For this example, US Customary units for acceleration due to gravity g = 32.17 ft/s², and density of water ⍴ = 1.940 slug/ft³

A ceiling mounted fire sprinkler
Image Source: WikiMedia Commons

Water for fire sprinkler systems in many large buildings are supplied by gravity. The water is often stored in large tanks on rooftops or near the buildings. To ensure there is substantial water pressure and disbursement from the sprinklers in case of an emergency, there must be at least 2160 lb/ft² of water pressure in the tank for a period of 10 minutes.

This is because during a fire, electrical systems may fail and it could take up to 10 minutes for the emergency generator and fire pump to be activated.

Suppose that the tank has a diameter of 20ft and the outlet has a diameter of 2.5inches, what height should design engineers specify for the tank to guarantee the required pressure?

Well, hydro-static pressure inside any vessel is given by...

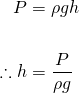
To have at least 2160 lb/ft² of pressure in the tank, the minimum height must be...

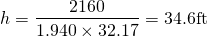
So after 10 minutes (600s) of the sprinklers being activated and draining the tank, we have by our general solution of equation (2)...

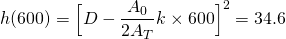
Before we solve for D...

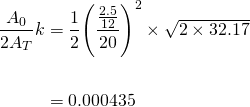
So...

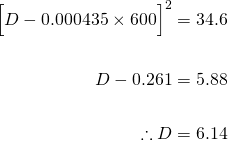
Therefore, the particular solution is...

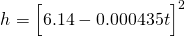
And finally, when the tank is full, at t = 0...

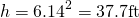
So, the reservoir tank for the emergency fire sprinkler system must be approximately 38ft tall to guarantee at least the required pressure for a duration of 10 minutes.

Assumptions and Experimental Evidence

Torricelli's law is accurate for liquids of negligible viscosity. Viscosity is a measure of a liquid's resistance to flow at a certain temperature. Under atmospheric pressure and typical room temperature, water is considered to have low viscosity.

Torricelli’s law becomes less and less valid as the viscosity of the liquid increases, as viscosity introduces losses to friction and swirling. Often a constant or coefficient c which is a specific property of the fluid, will be introduced to account for such losses. For instance…

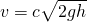
Another assumption is that the jet stream occupies the entire area of the hole as it leaves the reservoir. However for low viscosity fluids, the flow can be quite turbulent and the cross section of the jet may not occupy the entire area of the hole. J.C. Borda accounted for this by introducing a “contraction factor” of 0.6. Thus…

---

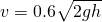
Credits:

All equations in this tutorial were created with QuickLatex

All graphs are created with www.desmos.com/calculator

Example 2 is a worked solution of a problem solving activity from Chapter 9 of Calculus, 5th Edition by Jame Stewart.

---

Below is a list of tutorials I've created so far on the subject of First Order Differential Equations:

1. Introduction to Differential Equations - Part 1

2. Differential Equations: Order and Linearity

3. First-Order Differential Equations with Separable Variables - Example 1

4. Separable Differential Equations - Example 2

5. Modelling Exponential Growth of Bacteria with dy/dx = ky

6. Modelling the Decay of Nuclear Medicine with dy/dx = -ky

7. Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky

8. Mixing Salt & Water with Separable Differential Equations

9. How Newton's Law of Cooling cools your Champagne

10. The Logistic Model for Population Growth

11. Predicting World Population Growth with the Logistic Model - Part 1

12. Predicting World Population Growth with the Logistic Model - Part 2

13. There's a hole in my bucket! Let's turn it into a cool Math problem!

---

Please give me an Upvote and Resteem if you have found this tutorial helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3

Tip me at PayPal: https://paypal.me/MasterWu