Modelling with Second Order ODE's: Undamped Free Oscillations
An undamped mass-spring system shown in Figure 1 below. These systems are commonly studied in mechanical engineering and mathematics. They are purely theoretical because they neglect damping forces.
A true system has damping forces because their free oscillations always eventually come to a stop. But, as I'll explain, this particular system will keep oscillating forever, or until some force interrupts it.
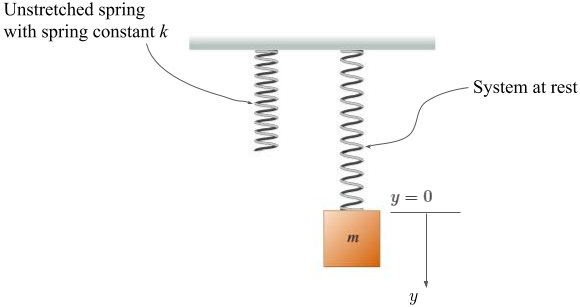
Figure 1. The mass-spring system
From Figure 1, suppose we have an elastic coil spring hanging from a ceiling with a mass attached to its free end.
Now this is a linear spring with spring constant k, and as such, it obeys Hooke's Law. The spring is able to resist both tension (extension) and compression.
Also suppose that the system is free from any effects of air resistance or other dampening effects. Therefore energy is purely transferred between the spring and the mass.
Before we begin to solve this problem, let's define a reference frame, where the downward direction is the positive y-direction, primarily because it is the same direction that gravity pulls. Also, let y = 0 be the equilibrium position of the top surface of the mass.
According to Hooke's Law, when the mass is pulled down by a distance (or displacement) y, the spring produces a force opposing the displacement of F = -ky. This is illustrated in Figure 2 below.
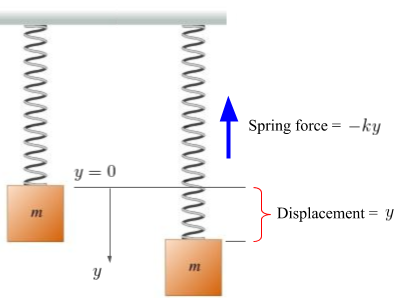
Figure 2. Stretched spring
So from Figure 2, we have...

The spring also causes an upward force on the mass of F = -ky.
Now force, according Newton's Second Law, can also be expressed classically as F = ma.
Thus...

Acceleration can be expressed as the second derivative of displacement with respect to time, thus we can write equation (1) as...
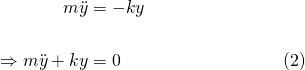
Equation (2), is a homogeneous, linear, second-order ODE with constant coefficients. And as such, we can find solutions using the characteristic equation...
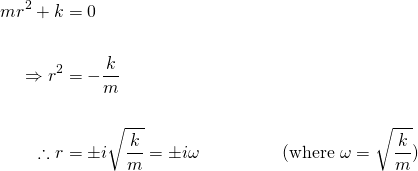
The roots of the characteristic equation are pure imaginary, and as such, according to equation (11) of the previous post, the general solution is...
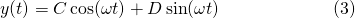
Note the greek letter ω (omega) in equation (3) denotes the angular frequency of the solution.
The motion described by the general solution is harmonic oscillation or simple harmonic motion.
What this is means is, the mass will oscillate indefinitely (as there is no energy dissipation by damping effects) when it is perturbed from its equilibrium position. The mass will freely oscillate at its natural frequency, which (in Hertz, or Hz) is...
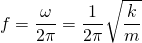
To find the unknown coefficients C and D, we need initial values. Let's solve for these coefficients algebraically first...
Suppose we have the initial displacement and velocity as...

We use the first initial condition to find C...
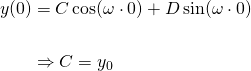
Now we use the second initial condition to find D...
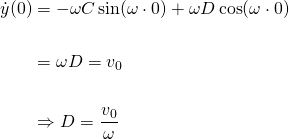
Ok, now that we have solved for the constants, the particular solution is...
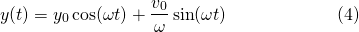
But that's enough algebra. Let's have a look at the physical behaviour of the solution when the mass is perturbed from it's equilibrium position.
The ways to do this are: giving the mass an initial position that is not the equilibrium position; giving the mass an initial velocity, or both.
Initial displacement problem
So suppose we have a system with the following parameters...
From this information, we can calculate the angular frequency of the oscillations as...
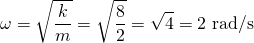
And from this, the natural frequency is...
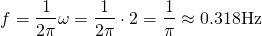
Thus the particular solution is...
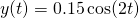
The behaviour of this solution is depicted in Figure 3 below.
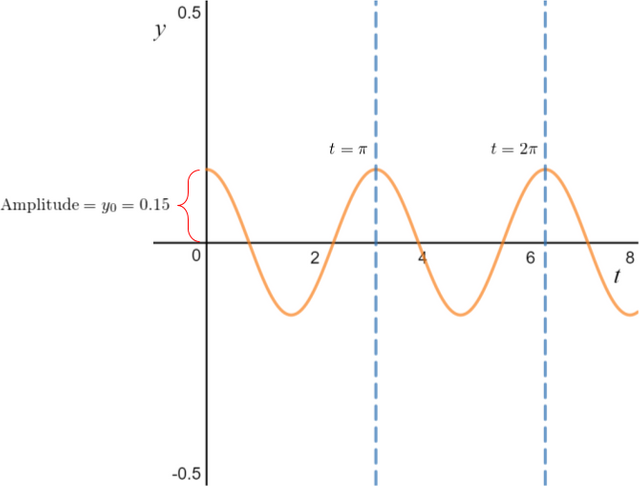
Figure 3. Behaviour of the initial displacement problem
Note how the amplitude of the oscillation, which is the maximum displacement from the equilibrium position, is determined by the initial displacement 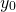 .
.
Figure 4 below shows the behaviour of the solution with varying values of 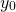 .
.
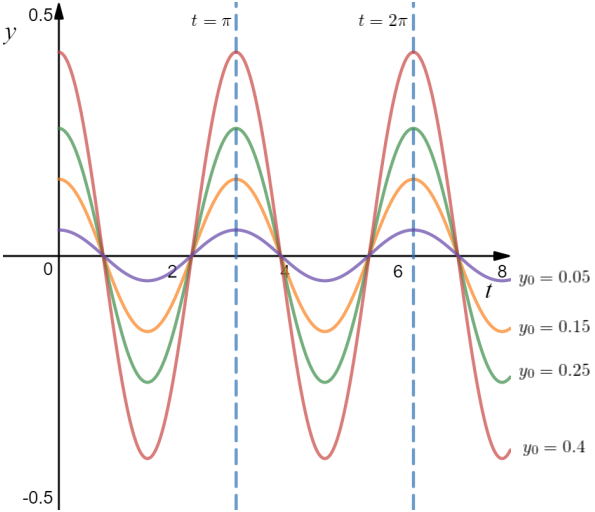
Figure 4. Behaviour with different values of initial displacement
As you can see from Figure 4, regardless of the initial displacement or amplitude of oscillation, the period and natural frequency remains the same.
Initial velocity problem
Let's see what happens under a different set of initial conditions. Suppose that...
The particular solution becomes...
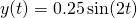
The behaviour of this solutions is depicted in Figure 5.
Figure 5. Behaviour of the initial velocity problem
Note how when we assign an initial velocity and a zero initial displacement, the oscillations are simply a phase shift of the initial displacement problem (with no initial velocity) to the right by π/4.
FIgure 6 below shows the behaviour of the solution with various values of initial velocity 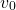 ...
...
Figure 6. Behaviour with different values of initial velocity
As you can see, no matter how fast we begin the motion of the mass, the frequency of the oscillations remain the same. Only the amplitude changes.
Initial displacement and initial velocity problem
Now let's see what happens when we have both initial conditions. The equivalent of the particular solution (4) can be rewritten as follows...
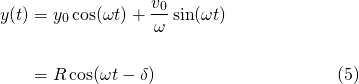
where...
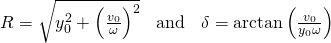
Suppose we have the following scenario...
Hence...
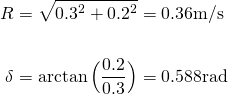
Thus the particular solution for this set of initial conditions is...
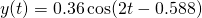
Figure 7 depicts the behaviour of this particular solution...
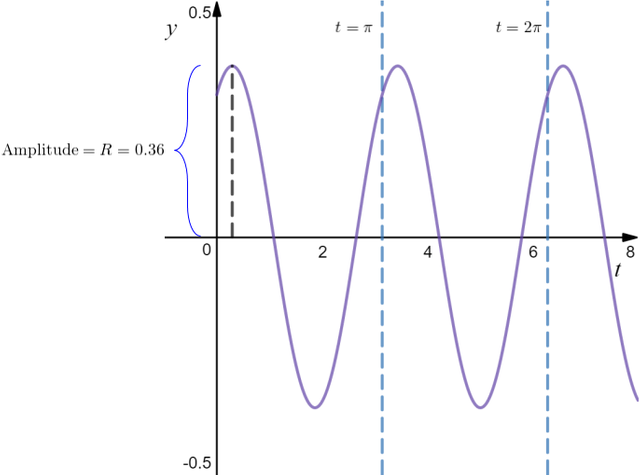
Figure 7. Behaviour of the combined initial displacement and velocity problem
Figure 8 below show what happens to the particular solution as the initial velocity varies from positive to negative.
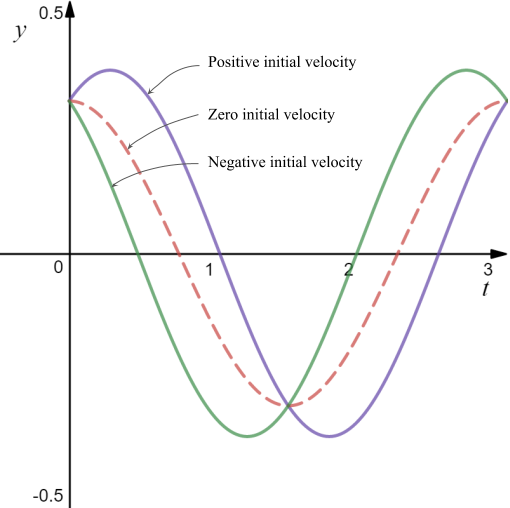
Figure 8. Behaviour of the solution for varying initial velocities.
In the next post, we'll look at what happens when we introduce damping into the model.
Credits:
All equations in this tutorial were created with QuickLatex
All graphs were created with www.desmos.com/calculator
First Order Differential Equations
- Introduction to Differential Equations - Part 1
- Differential Equations: Order and Linearity
- First-Order Differential Equations with Separable Variables - Example 1
- Separable Differential Equations - Example 2
- Modelling Exponential Growth of Bacteria with dy/dx = ky
- Modelling the Decay of Nuclear Medicine with dy/dx = -ky
- Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky
- Mixing Salt & Water with Separable Differential Equations
- How Newton's Law of Cooling cools your Champagne
- The Logistic Model for Population Growth
- Predicting World Population Growth with the Logistic Model - Part 1
- Predicting World Population Growth with the Logistic Model - Part 2
- What's faster? Going up or Coming Down?
First order Non-linear Differential Equations
- There's a hole in my bucket! Let's turn it into a cool Math problem!
- The Calculus of Hot Chocolate Pouring!
- Foxes hunting Bunnies: Population Modelling with the Predator-Prey Equations
Second Order Differential Equations
- Introduction to Second Order Differential Equations
- Finding a Basis for solutions of Second Order ODE's
- Roots of Homogeneous Second Order ODE's and the Nature their Solutions
- Modelling with Second Order ODE's: Undamped Free Oscillations
Please give me an Upvote and Resteem if you have found this tutorial helpful.
Please ask me a maths question by commenting below and I will try to help you in future posts.
Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu
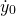
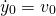
Good to have you back. All the cool stuff happens when your consider 2 springs attached to each other. Maybe it is nice to do a post about that as well :)
It's good to be back! Don't worry, I'll definitely be posting about coupled systems as I advance this topic :)
Congratulations! Your post has been selected as a daily Steemit truffle! It is listed on rank 12 of all contributions awarded today. You can find the TOP DAILY TRUFFLE PICKS HERE.
I upvoted your contribution because to my mind your post is at least 8 SBD worth and should receive 94 votes. It's now up to the lovely Steemit community to make this come true.
I am
TrufflePig, an Artificial Intelligence Bot that helps minnows and content curators using Machine Learning. If you are curious how I select content, you can find an explanation here!Have a nice day and sincerely yours,

TrufflePigThank you @trufflepig