Modelling the Decay of Nuclear Medicine with dy/dx = -ky
Inasmuch as the differential equation dy/dx = ky models exponential growth, it follows that dy/dx = -ky models exponentially decaying processes.
A exponential decay process, which is a slowing reduction in quantity over time, follows the equation y = Ae-kx. The decay constant, which governs the rate of decay, is given by k. This family of solutions is shown in the graph below...
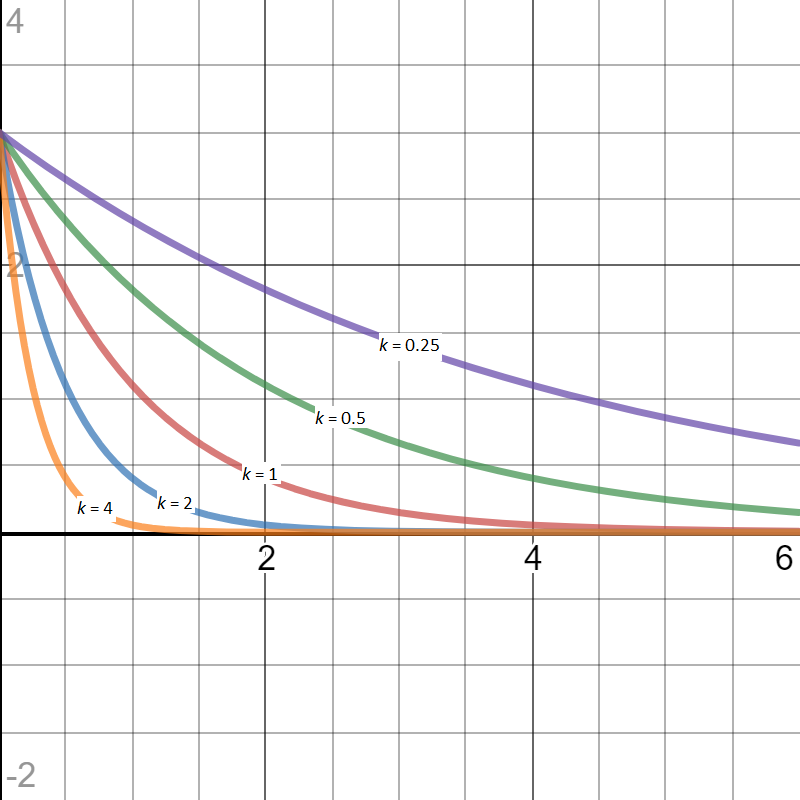
Drawn with Desmos
These curves may aptly represent for example: a radioactive decay process; the amount of charge remaining in a capacitor as current flows out; the temperature of a hot surface undergoing forced convection cooling.
In fact, let's solve a radioactive decay problem:
The half-life of a radioactive element used in the treatment of cancer is 4 hours. 12mg are produced at 10AM. Use a differential equation to find an expression for the amount present at time t, and thus the amount remaining at 4PM.
Let M be the amount (i.e. mass in mg) of the radioactive element as it changes over time t. The decrease in M over time can be expressed as:
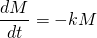
Solving this differential equation we get the general solution...
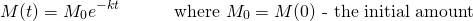
We are given that the half-life of the radioactive element is 4 hours. Half-life describes the time it takes for a substance to decay half the initial amount. Thus...
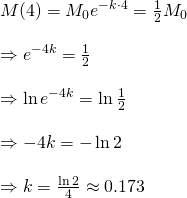
Therefore, our equation for modelling this radioactive decay is...
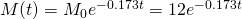
At 4PM, we are 6 hours past 10AM. Thus the quantity remaining is:
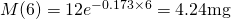
For a detailed explanation please watch the video below.
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
I would really appreciate any small donation which will help me to help more math students of the world.
Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu
Thank you :)