Differential Equations: Order and Linearity

Hey there Steemit! I haven't posted in a while... usual excuses: too busy, distracted by life, etc. But it's good to be back and seeing the community rocking strong!...

In part 1, we established that a differential equation is any equation that contains the derivative of an unknown function. We also established that differential equations are one of the most important and useful applications of Calculus in modelling real world problems mathematically.

Now, let's have a look at the order and linearity of differential equations.

Order of Differential Equations

Let's describe this with the classic example of a mass on the end of a spring, of course in ideal conditions where we ignore friction, dampening and air resistance...

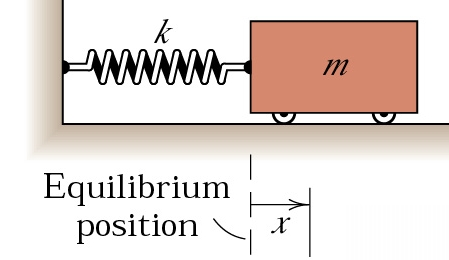
Image Source

When the mass is pulled to the right by a distance x, according to Hooke's Law, the force in the spring pulling the mass back toward the equilibrium position (i.e. the resisting force) is given by:

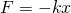
...where k is the spring constant.

Now, according to Newton's Second Law of motion, the force on the mass F can be expressed as the mass times its acceleration, which is the second derivative of its displacement with respect to time. That is...

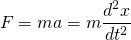
Thus...

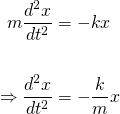
And rearranging...

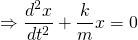
...we get the differential equation which describes the motion of the mass-spring system.

So, we have the second derivative of the displacement x, as well as x in the above equation. For completeness, let's re-write the differential equation as...

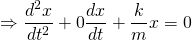
What we have above is a linear, second-order differential equation. We won't solve this equation yet, but our goal is to get a solution or a set of solutions for the known function x(t).

The order refers to the highest derivative of the unknown function x(t).

Linearity

Linearity for differential equations is a dichotomous term. A differential equation is either linear or non-linear.

For a function y(x), if its power (or degree), or any of the powers of its derivatives are not equal to 1, the differential equation is considered to be non-linear.

For instance, the equation...

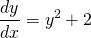
Is a non-linear, first-order differential equation because the power of the function that we want to solve for, y(x) is 2 (which is > 1).

Generally, a differential equation is considered linear if it can be written in the form:

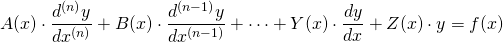
In the above equation, the coefficients A(x), B(x)... etc., can be any constant, or continuous function. Only the function of interest y(x) is used to determine linearity.

For instance, the equation....

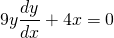
...is also a first-order, non-linear differential equation because it cannot be reduced to the linear form.

That will complete this tutorial. Below is a list of tutorials I've created so far on Differential Equations:

1. Introduction to Differential Equations - Part 1

2. Differential Equations: Order and Linearity

3. First-Order Differential Equations with Separable Variables - Example 1

4. Separable Differential Equations - Example 2

5. Modelling Exponential Growth of Bacteria with dy/dx = ky

6. Modelling the Decay of Nuclear Medicine with dy/dx = -ky

7. Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky

Please give me an Upvote and Resteem if you have found this tutorial helpful.

Please ask me a math question by commenting below and I will try to help you in future tutorials.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu