Modelling Car Suspension with ODE's: Damped Free Oscillations Part 2
In the mathematical modelling of the mass-damper-spring system (Figure 1), we've explored the underdamped case in the previous post.
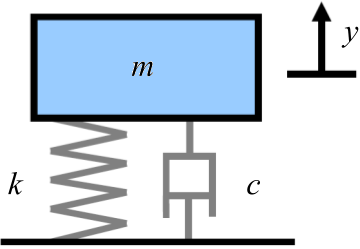
Figure 1. Schematic of the mass-damper-spring system (adapted from Wikimedia Commons)
We seen that with an under damped suspension system (case I), a car can wallow up and down whenever it goes over a speed bump, making it very difficult for the driver to control the vehicle.
Before we explore the case II, critical damping, let's recap the equation of motion for the mass-damper-spring system...
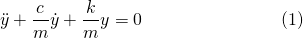
where:
...we can have 3 different cases...
| Case I |  < 0 < 0 |
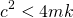 |
Under damping |
| Case II |  = 0 = 0 |
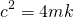 |
Critical damping |
| Case III |  > 0 > 0 |
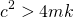 |
Over damping |
Case II: Critically Damped
Critical damping is the border case between oscillatory (under damped) and non-oscillatory (over damped) motions.
Let's take explore our car suspension model with the damper tuned to be critically damped. The parameters from the previous post...
- sprung mass m = 300kg
- spring constant k = 1200N/m
- initial displacement
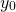 = 0.15m
= 0.15m - initial velocity
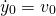 = 0m/s
= 0m/s
The system is critically damped when...
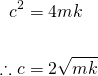
Substituting above parameters, we need to tune the damper to...

A diagram of the system is shown in Figure 2 below...
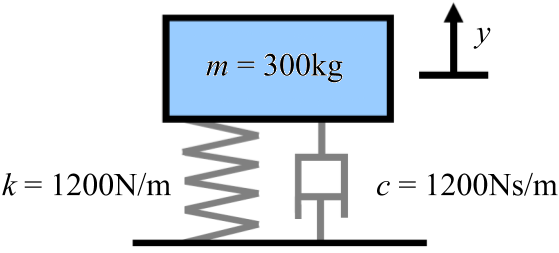
Figure 2. Suspension schematic with parameters required for critical damping
Now that we have the damping coefficient for the critically damped case, substituting these into equation (1), the equation of motion becomes...
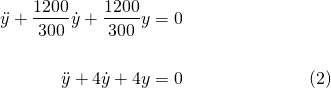
The characteristic equation of (2)...

The only root of equation (3) is...
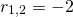
Now according to equation (8) of Post #3, the general solution is...
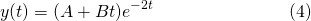
Applying the first initial condition (initial displacement)...
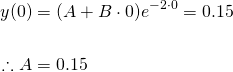
The first derivative of the general solution, equation (4) is...
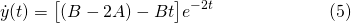
Now we can apply the second initial condition (initial velocity)...
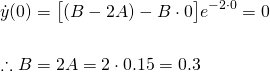
Therefore, the particular solution is...
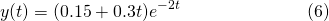
The behaviour of the particular solution is shown in Figure 3...
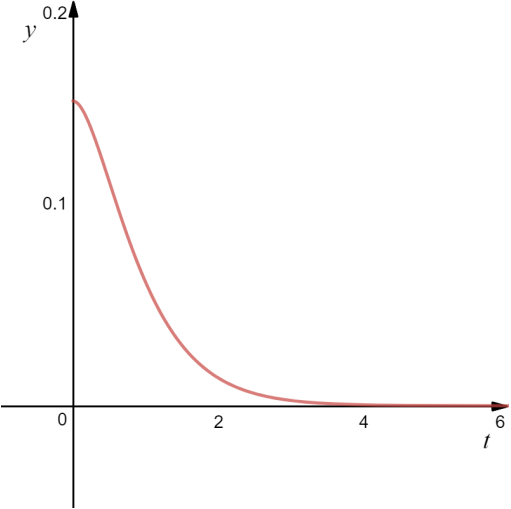
Figure 3. Behaviour of the suspension system with
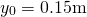 and
and 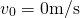
As you can see, the car pretty much returns to its equilibrium position in less than 4 seconds, which is quite a slow response for most real-world applications.
Exploring the initial value problem
Let's now explore the solution with a few different permutations for the initial conditions...
Substituting this values into equation (5)...
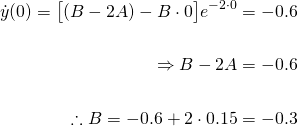
This gives rise to the particular solution is...
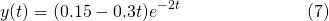
What about the following?...
This gives rise to the particular solution...

And the following permutation...
...gives rise to the particular solution...
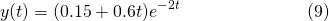
All of the above solutions are superimposed in Figure 4...
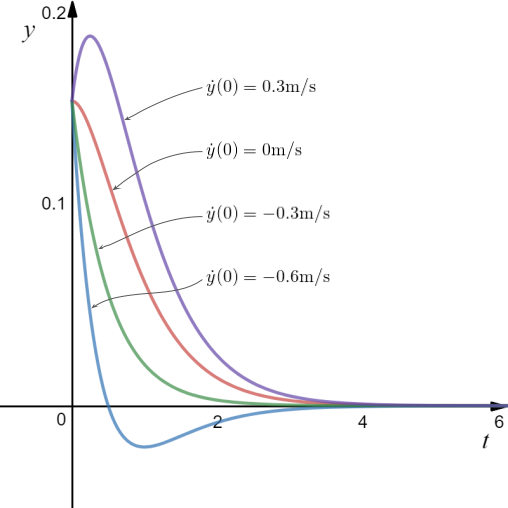
Figure 4. Various particular solutions to the critically damped car suspension problem.
Finally, let's see how the suspension behaves with zero initial displacement, but a non-zero initial velocity. For instance...
Again, from equation (5), we have...
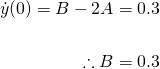
...giving rise to the particular solution...

A few solutions showing the behaviour of the mechanism with varying values of 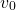 ...
...
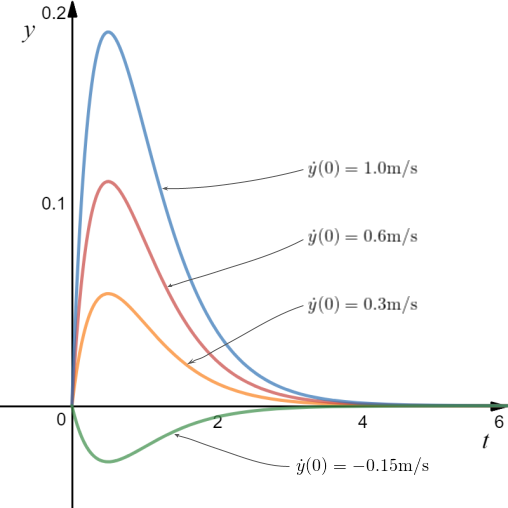
Figure 5. Various particular solutions to the critically damped car suspension problem.
Discussion about the above case...
Critical damping is what car manufacturers aim for in most cases. As we have seen with under damping, the residual vibrations that occur after hitting a bump can be very dangerous in terms of steering and car control. It can also cause passengers who are susceptible to motion sickness to become ill.
With over damping, which we will explore in the next post, the shock absorber is stiff and sluggish, which means it is slow to respond to bumps. This means that bumps are not absorbed as much and car returns to its equilibrium position slowly, making the ride quite uncomfortable. It feels like a car with no suspension, and may compromise the car's grip on rougher roads, because the wheels are in less contact with the ground at certain times (the car might do a "jump" when it hits a bump).
As I have mentioned previously, the parameters used for the this particular suspension set up is quite "soft" and "squishy" for most real-world applications. We have a soft spring at 1200N/m, and the critical damping coefficient for this softly sprung car will dissipate a bump of 15cm in about 4 seconds.
Credits:
All equations in this tutorial were created with QuickLatex
All graphs were created with www.desmos.com/calculator
First Order Differential Equations
- Introduction to Differential Equations - Part 1
- Differential Equations: Order and Linearity
- First-Order Differential Equations with Separable Variables - Example 1
- Separable Differential Equations - Example 2
- Modelling Exponential Growth of Bacteria with dy/dx = ky
- Modelling the Decay of Nuclear Medicine with dy/dx = -ky
- Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky
- Mixing Salt & Water with Separable Differential Equations
- How Newton's Law of Cooling cools your Champagne
- The Logistic Model for Population Growth
- Predicting World Population Growth with the Logistic Model - Part 1
- Predicting World Population Growth with the Logistic Model - Part 2
- What's faster? Going up or Coming Down?
First order Non-linear Differential Equations
- There's a hole in my bucket! Let's turn it into a cool Math problem!
- The Calculus of Hot Chocolate Pouring!
- Foxes hunting Bunnies: Population Modelling with the Predator-Prey Equations
Second Order Differential Equations
- Introduction to Second Order Differential Equations
- Finding a Basis for solutions of Second Order ODE's
- Roots of Homogeneous Second Order ODE's and the Nature their Solutions
- Modelling with Second Order ODE's: Undamped Free Oscillations
- Modelling Car Suspension with ODE's: Damped Free Oscillations Part 1
- Modelling Car Suspension with ODE's: Damped Free Oscillations Part 2
Please give me an Upvote and Resteem if you have found this tutorial helpful.
Please ask me a maths question by commenting below and I will try to help you in future posts.
Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu

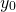
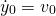
Excellent Mathematical description. Often hard to explain, but you did so with ease. Keep it up :)
Thank you @akeelsingh