Predicting World Population Growth with the Logistic Model - Part 2

In my last post, we solved an example problem for predicting the growth of the world's population using the logistic model. The resultant growth curve is shown below...

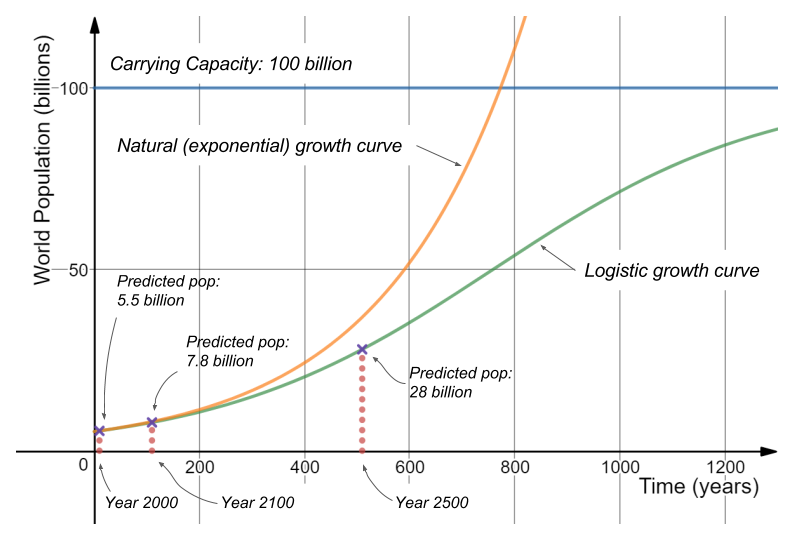Created with: www.desmos.com/calculator

The supposed upper limit of a population of 100 billion (called the "Carrying Capacity") is shown by the blue horizontal line.

We have the natural growth curve, which follows the exponential growth model, in orange. And we have the logistic growth curve shown in green.

We can see that the natural growth and the logistic growth curves track each other quite congruently at the beginning. They begin to diverge shortly after 110 years (the year 2100). The exponential growth curve continues to accelerate and become steeper, while the growth rate of the logistic curve slows and eventually decreases as the population heads toward its cap of 100 billion.

---

But now, what happens to the logistic growth curve when we halve the carrying capacity to K = 50 billion? Again, the general solution to the logistic equation is...

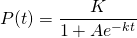
We find the coefficient A by the following formula...

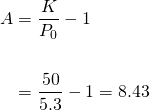
This time, due to a halving of the carrying capacity, we assume the "logistic coefficient" C(P) will have a significant influence on the result. At the beginning, its value is calculated as...

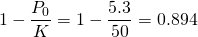
Now recall the logistic differential equation...

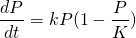
Substituting in the initial value for the logistic coefficient, we have...

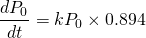
And from this, we can determine the growth factor k

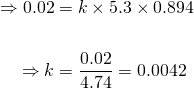
Knowing all of the above, we have the particular solution to this initial value problem as...

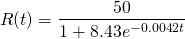
Ok, let's graph this and see how it compares with our earlier result...

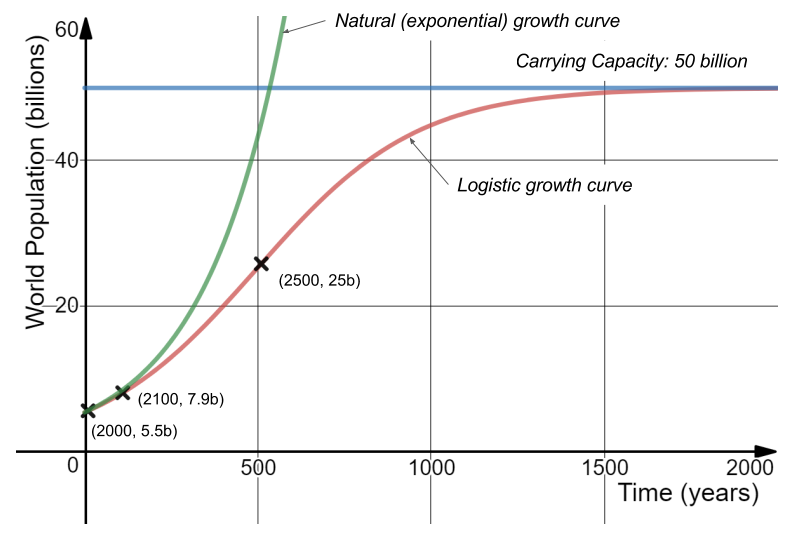Created with: www.desmos.com/calculator

It's a bit hard to visually see because I didn't use the same scales for generating the 2 graphs (apologies, my bad), but the most difference is the growth rate is more rapid at the beginning when we lower the carrying capacity, but it also decelerates faster as time goes on, and the population to levels off to the lowered carry capacity quicker.

On a final note for this post, there are always 2 equilibrium solutions for the logistic model with P(t) = 0 and P(t) = K.

These make physical sense because if we have a population of a species at 0, it will always be 0. Otherwise it always tends to the carrying capacity.

This problem was adapted from an exercise in Calculus 5th Edition by James Stewart.

---

Below is a list of tutorials I've created so far on the subject of First Order Differential Equations:

1. Introduction to Differential Equations - Part 1

2. Differential Equations: Order and Linearity

3. First-Order Differential Equations with Separable Variables - Example 1

4. Separable Differential Equations - Example 2

5. Modelling Exponential Growth of Bacteria with dy/dx = ky

6. Modelling the Decay of Nuclear Medicine with dy/dx = -ky

7. Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky

8. Mixing Salt & Water with Separable Differential Equations

9. How Newton's Law of Cooling cools your Champagne

10. The Logistic Model for Population Growth

11. Predicting World Population Growth with the Logistic Model - Part 1

12. Predicting World Population Growth with the Logistic Model - Part 2

---

Please give me an Upvote and Resteem if you have found this tutorial helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu