Predicting World Population Growth with the Logistic Model - Part 1

Here is a graph by Our World in Data depicting growth and predictions of world's population. As you can see, it follows the general trend of the logistic model.

Image Source

Let's do an example problem using the logistic model: The world's population was around 5.3 billion in 1990. Birth rates at that time was approximately 40 million per year, and death rates approximately 20 million per year.

Assuming that the carrying capacity for the world population is 100 billion, let's use the logistic model to:

• estimate the world population in the year 2000
• predict the world population in the years 2100 and 2500

Ok, first of all, let's write the logistic differential equation:

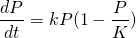
Let's assume the year 1990 is time t = 0. We have the growth rate:

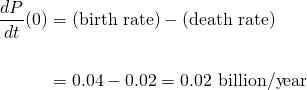
Now, taking into account the given parameters, in the beginning, the ratio P/K is quite small. And thus, the differential equation acts more like the natural growth, or the exponential model. That is...

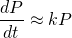
From this, we can solve for the growth factor k, which is one of the key pieces of this puzzle.

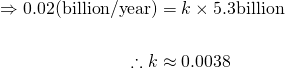
Excellent, now we have k, we also know the general solution to the logistic differential equation from our last post:

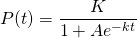
We have the initial population (initial value) of 5.3 billion and the carrying capacity of 100 billion. From this data, we can find the coefficient A by rearranging the above equation and setting t = 0...

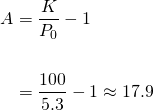
And thus we have the particular solution:

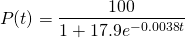
Alright. Now to estimate the world population in the year 2000, when t = 10:

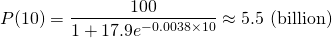
This is a conservative estimate of the world population in the year 2000, as the actual population was around 6.1 billion. Our estimate was about 10% less than the actual, and predicted a population increase of only 200 million in those 10 years. Therefore there may be some parameters which we may not have correct in our model.

But let's assume our model and data is correct. What is the population going to be in 2100, when t = 110 years?

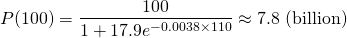
The world's population is predicted to be roughly 8 billion in 2100, which may also be conservative considering it is currently at 7.6 billion.

And in the year 2500? This is t = 510 years from 1990.

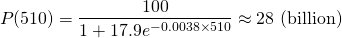
According to our model with its current parameters, world population is expected to be about 28 - 30 billion. This is probably too far into the future to be an accurate prediction.

That'll do it for Part 1. In Part 2, we'll look at our solution graphically and see how our results change if we change the carrying capacity to 50 billion.

This problem was adapted from an exercise in Calculus 5th Edition by James Stewart.

Below is a list of tutorials I've created so far on the subject of Differential Equations:

1. Introduction to Differential Equations - Part 1

2. Differential Equations: Order and Linearity

3. First-Order Differential Equations with Separable Variables - Example 1

4. Separable Differential Equations - Example 2

5. Modelling Exponential Growth of Bacteria with dy/dx = ky

6. Modelling the Decay of Nuclear Medicine with dy/dx = -ky

7. Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky

8. Mixing Salt & Water with Separable Differential Equations

9. How Newton's Law of Cooling cools your Champagne

10. The Logistic Model for Population Growth

11. Predicting World Population Growth with the Logistic Model - Part 1

Please give me an Upvote and Resteem if you have found this tutorial helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu