Physics - Electromagnetism - Magnetic force applied on Current-Carrying Conductors
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into the magnetic force that gets applied on current-carrying conductors. To understand this you should first know what magnetic fields and forces are, which means that I suggest you to go read those posts of the series. So, without further do, let's get started!
Current-Carrying Conductor and Magnetic field
We know that magnetic fields are generated by magnets, but this is not the only source of them. Current-Carrying Conductors/Wires can also create magnetic fields, which is something that we will get into later on during this series... Either way this all again shows us that Electricity and Magnetism are very closely binded together. The thing is Current-Carrying wires don't only create magnetic fields, but are also affected by magnetic fields. When a current-carrying wire is placed in a magnetic field the magnetic filed exerts a force on the wire. Until now we saw that Forces are measured in Newton's (N) and that the magnetic field strengh or flux density is measured in Tesla (T).
Magnetic force exerted on Current-Carrying Conductors
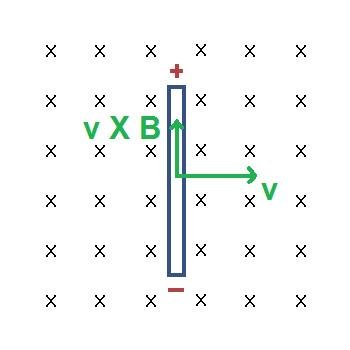
Let's consider a long, straight current-carrying wire that is placed inside of a magnetic field. The force exerted on that wire is proportional to the strength of the field, the amount of current and the length of the wire. The equation looks like this:
where:
- F is the force acting on the current-carrying conductor
- B the magnetic flux density or magnetic flux density
- I the magnitude of the current flowing through the conductor
- l the length of the conductor
- θ the angle the conductor makes with the magnetic field (remember that only perpendicular components are being affected)
An easy way of remembering this equation is by thinking of the name "Bill"! :P
Having the force be proportional to sinθ we can clearly see that the force is maximum when the conductor is perpendicular (θ = 90°) to the magnetic field. The force is zero when the conductor is parallel to the magnetic field, exactly as we saw last time with charged particles.
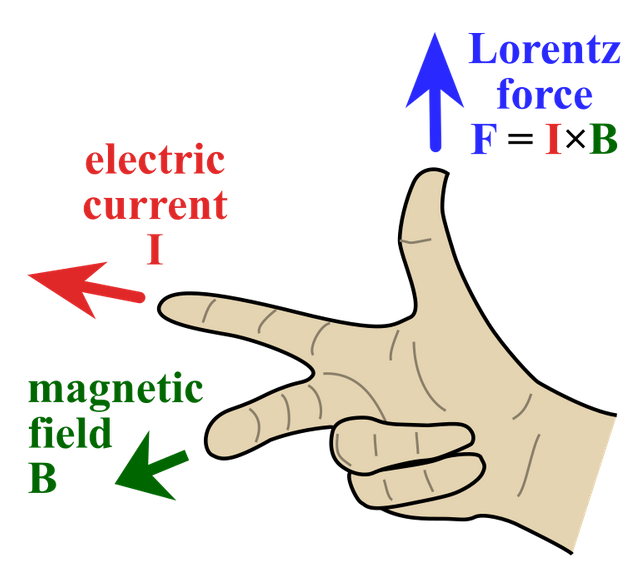
The direction of the force can be found again using the right-hand rule. The velocity now "switches" with the current (think of velocity and current showing the actual trajectory of the charge) and so the index finger now points in the direction of the current, the middle finger in the diretion of the field and the thumb shows us the direction of the magnetic force. All this is of course only true if the current is "positive". Here a diagram so that you understand it a little bit better:
Image source: https://commons.wikimedia.org/wiki/File:Right_hand_rule_cross_product_F%3DI%C3%97B.svg
Proof of the equation
So, ok all this is fine, but how do we end up with this equation?
Until now we saw that the magnetic force on a "single" charge is given by:
where:
- F is the magnetic force applied to the charged particle
- q is the magnitude of charge that the particle is is carrying
- v is the so called drifting velocity of the particle
- B is the magnitude of the magnetic field
The direction of that force was given by the right-hand rule (switch current with velocity in the previous diagram...).
In Current and Resistance we saw that the current I that passes through a section with area A is described as:
where:
- n is the number of charge carriers
- q is the magnitude of charge of each of those charges
- A is the area of the section
- v is the drifting velocity of each charge carrier
Suppose a wire of length l and a density of n charges per unit of volume in each nAdl section. The total number of charges is of course N = nV, where V is the volume of the wire, which is Al. By combining all these equations we can calculate the total magnetic force applied on the current which is:
Note that vector units are the length/trajectory and magnetic field vectors and so the correct "order" of the equation is IlB or lBI and not BIl, but it's easier to remember it as BIl. Also, for all this we considered a uniform magnetic field and l and B are also considered to be perpendicular (no sinθ part)...
Another interesting way of proving
The basic magnetic force exerted on a charged particle is given by:
Velocity is of course the distance travelled over time and so we get:
Current is defined as the charge that passes a section over time and so we get:
Cool hah?
Take-backs
So, what have we learned today?
- Magnetic fields affect current-carrying conductors by exerting magnetic force
- This magnetic force is calculate by the equation: F = IlBsinθ
- Similar to charged particles the magnetic field doesn't affect the wire/conductor when it's parallel to the magnetic field.
- The magnitude of the force is maximum when the wire/conductor is perpendicular to the field
- The direction of the force is given by the right-hand rule
REFERENCES:
- https://study.com/academy/lesson/understanding-forces-on-current-carrying-wires-in-magnetic-fields.html
- https://www.miniphysics.com/force-on-current-carrying-conductor.html
- https://courses.lumenlearning.com/physics/chapter/22-7-magnetic-force-on-a-current-carrying-conductor/
- https://pressbooks.bccampus.ca/collegephysics/chapter/magnetic-force-on-a-current-carrying-conductor/
- https://phys.libretexts.org/TextBooks_and_TextMaps/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_II_-_Thermodynamics%2C_Electricity%2C_and_Magnetism_(OpenStax)/11%3A_Magnetic_Forces_and_Fields/11.4%3A_Magnetic_Force_on_a_Current-Carrying_Conductor
- http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/forwir2.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism
The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion
Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens
And this is actually it for today's post!
Next time we will cover the Magnetic force and torque that's gets applied on current loops.
Bye bye!

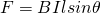
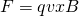
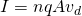
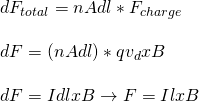
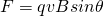
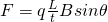
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
upvote for me please? https://steemit.com/news/@bible.com/2sysip