Physics - Electromagnetism - Electric current, resistance and emf exercises
Custom Thumbnail
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into the Exercises for current, resistance and emf that we covered in the previous 5 posts of this series. Those exercises or mathematical applications will only make sense if you already know about current, resistance, potential and emf.
Also, the promised explanation of the conductivity of materials more in-depth will not be done now and I will leave it for later when we get into Atomic Physics...
So, without further do, let's get straight into it!
We will get into examples for each of those three topics...
Electric current:
Let's consider a conductive wire with:
- a diameter d = 1mm
- a constant flowing current I = 2A
- a "free" electron density n = 9 x 10^28/m^3
Calculate:
- The electric current density J of the wire
- The "drifting" velocity (vd) of the electrons
1.
From theory we know that the electric current density is given by the equation:
The second "part" of the equation requires us to know:
- the density of charge n (which is given to us)
- the charge of an electron (which is a constant value that is of course also known)
- the drifting velocity (which is to be calculated in the second question)
That's why we will use the "second" part for question 2.
For the first "part" we have to find the area A of the cross-section of the wire, which is pretty easy considering that the wire is a cylinder. The Area of the circle cross-section is given by A = πr^2, where r is the radius. The value given to us is the diameter which of course is twice the radius and so d = 2r, which means tha the radius of the circle is r = 1mm/2 = 0.5mm. The final value of the area is:
And so the current density is:
2.
Knowing the current density, density of electrons and charge of an electron we can now calculate the drifting velocity with ease. The current density is J = 2.547x10^6 A/m^2, density of electrons is given to us as n = 9 x 10^28/m^3 and the charge of an electron is of course 1.6x10^-19C, which is a physics constant. That way the drifting velocity is:
In other applications we might have to calculate the current, radius, diameter, density of charge etc. and so the actual way of applying the current theory doesn't differentiate by a lot...Also don't forget that the current is the charge per time unit, which means that some time and the amount of charge that passes in that time can also be useful information for calculating current, speed etc.
Electric resistance:
Let's get into 2 applications which are strongly connected two the 2 ways of calculating or using resistance.
Application 1
Consider the conductive wire that we had before that had:
- a diameter d = 1mm (radius 0.5mm)
- a cross-section area A = 7.85x10^-7 m^2
- an electric current I = 2A
- a charge density J = 2.547x10^6 A/m^2
Calculate:
- the electric field's magnitude
- the potential difference of two points that have a distance l = 50m
- the resistance of a 50m section of the conductive wire
The electric resistivity ρ of the wire is:
1.
From the definition of resistivity we know that ρ = E/J which means that the calculation of the electric field can be done very fast like that:
2.
In a previous post we proved that the electric field can be calculated using E = V/d when having an uniform electric field, which is clearly the case for this ideal wire and so by replacing d with the distance l which the two points are apart we get:
3.
The Resistance can be calculated in two ways:
- Ohm's law which is R = V/I, where V is the potential difference of 50m that we already calculated and I is also known
- The relation of resistivity and resistance which is R = ρl/A, where we also know everything
Let's do both to see if we get the same result!
The second one is a little bit different, cause I approximated the result of the potential and electric field a lot, which means that we had some error...
Application 2
Let's consider a wire with thermal (temperature) coefficient:
and with a resistance of 1Ω at a temperature of 20 °C.
Calculate the resistance at 0 °C and 100 °C.
By using the formula of the theory we get:
You can see that the resistance drops when the temperature drops and increases when the temperature increases, which is exactly what we expected, cause the thermal coefficient is positive.
Electromotive Force (EMF):
There are 3 main cases for the energy source which are:
- Open circuit
- Closed circuit
- Short circuit
Let's consider a battery with EMF ε = 12V and internal resistance r = 2Ω.
Calculate:
- The voltage at the terminals of the battery
- The current of the circuit
- The power/wattage of the circuit
For the closed circuit consider a resistance of R = 4Ω and for the short circuit a total resistance R = 0.
Let's get into each circuit on it's own.
1.
When having an open circuit there is no current, cause one of the requirements for having a constant current flow is having a closed circuit. Which means that I = 0A. The voltage outside of the battery is of course equal to the EMF and so V = ε = 12V, where the voltage at the internal resistance r is of course 0, cause no current flows through. Having no current if of course have no power/wattage and so P = 0W.
2.
The current that flows through the closed circuit is calculated by I = V/R, where V is the EMF and R is the total resistance which is equal to R+r.
That way the current is:
The potential difference at the terminals of the battery is equal to the total voltage that the emf actually supplies the circuit with. This means that we have to remove the voltage of the internal resistance which is V = Ir and so the potential difference is:
Let's also find the voltage at the terminals of the resistor. Supposing that the wire is ideal it has no resistance, but the only resistance is the resistor of 4Ω. This means that the voltage at the sides of the resistor is:
I don't really specified what I mean by power/wattage, so let's calculate everything! The rate in which the stored chemical energy of the battery is converted into electrical energy is:
The heat dissipation of the battery is:
The power consumption of the resistor is:
which can also be calculated using P = VI.
That way we can clearly prove the equation that I pointed out last time:
that clearly proves us the consistency of our results!
3.
Having no resistance the potential difference at the terminals "outside" of the battery is V = 0. That way the current is calculated as:
which is 3 times the value that we had before!
The rate in which chemical energy is converted to electric energy in the battery is now:
The heat dissipation of the internal resistance r is:
And so all the power is converted into heat inside of the battery's resistance, which again shows us that the polar voltage or voltage outside of the battery is zero. Short circuiting the battery is not good, cause it destroys them and also creates a larger current which is not so good!
REFERENCES:
All the mathematical equations that I had in this post where drawn using quicklatex to make them look better! The small explanations of the steps that I take can also be found as actual theory in the previous 5 posts...
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
And this is actually it for today's post!
Next time we will start getting into direct current, which means that we will cover Kirchoff's Laws and R-C circuits throughout the next posts of Electromagnetism.
Bye!


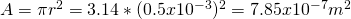
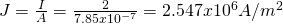
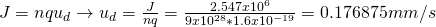
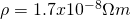
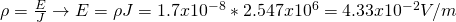
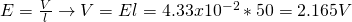
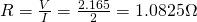
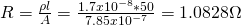
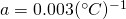
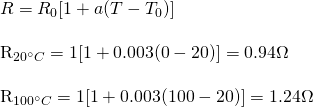
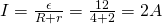
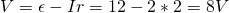
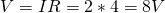
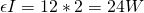
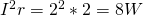
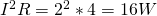
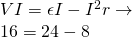
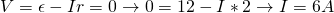

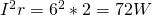
As a follower of @followforupvotes this post has been randomly selected and upvoted! Enjoy your upvote and have a great day!