Physics - Electromagnetism - Resistor Combinations
Image source: https://www.electronicshub.org/
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Resistor Combinations. I highly suggest you to read the post about Resistors/Resistance and the combination of resistors is also quite similar to the combination of capacitors which might also be interesting to check out. So, without further do, let's get started!
Quick reminder of resistors
Resistors are circuit elements that implement electrical resistance. They are useful for reducing current flow, adjusting signal levels, dividing voltages etc. The resistance of them changes with temperature, time and voltage. A very useful law that applies to ideal resistors (ohmic-resistors) is Ohm's law that states V = I*R, which means that the voltage (V) across a resistor is proportional to the electric current (I) times the resistance (R) of the resistor. Of course the resistance is calculated in Ohm's (Ω) which is equal to V/A (volt/ampere), but a lot of times we talk about smaller or larger resistances of mΩ, kΩ or even MΩ. What makes resistors very useful is the power dissipation in heat (used for hair dryers, boilers etc.), where the actual power consumed in watts is calculated by: 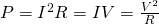
[1]
Resistor Combinations
Because resistors are so useful most circuits have resistors, but there are mostly more then one of them. The resistors can be connected in many different ways. The main two ways of connecting components and so resistors in electronic circuits is in a serial or parallel combination. We can also have more complex circuits which are "Mixed resistor circuits" and contain a mix of the previous two. Depending on the combination we can calculate the total or equivalent resistance of all those resistors combined. We actually only have mathematical formulas for serial and parallel combination, but can easily apply those "in steps" to solve more complex connections.
So, let's get into each combination on it's own to understand the concepts behind them.
Series combination
We say that resistors are connected "serially" if the current flows through them sequentially. This means that all resistors have the same current which is equal to the current of the battery (or energy supply in general). According to Ohm's law the voltage drop of each resistor is V = IR, where I is the same for all the resistors and R is the resistance of teach individual resistor. The sum of all the voltages is equal to the output of the energy source and so V = V1 + V2 + ... Because of the conservation of charge: V = IR1 + IR2 + ... = I(R1 + R2 + ...) which means that the total or equivalent resistance R is equal to the sum of each individual resistance Ri and so: R = R1 + R2 + ...
And so for series circuits:
- The current is the same for each resistor
- The some of voltage drop is equal to the voltage of the energy supply
- The total/equivalent resistance is equal to the sum of the individual resistances
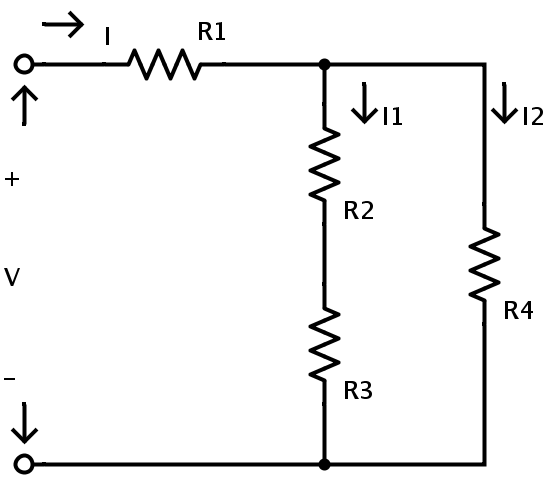
Parallel combination
We say that resistors are connected "in parallel" if they are all wired to the same voltage source. This means that each resistor is connected direcly to the voltage of the energy supply (battery) and has the full voltage of the source applied to it. That way each resistor draws the same current that it would if it was connected to the voltage sourrce on it's own. From Ohm's law we have that the individual current flow through each resistor is I = V/R where V is the same for all the resistors and so I changes depending on the resistance R of each resistor. From the conservation of charge we imply that the total current is I = I1 + I2 + ... and so equal to the sum of each individual current. Substituting the current I with the individual currents we get:
And so the total/equivalent resistance is calculated as:
And so remember that for parallel circuits:
- The voltage drop is the same at each resistor
- The total current is equal to the sum of each individual current
- The "converse" total/equivalent resistance is equal to the sum of the "converse" resistances of each resistor.
Mixed combination
When having more complex connections we mostly have combinations of series and parallel. We can reduce those combinations by finding the single equivalent resistance of each part that we identify as series or parallel. By continuing on this process we will finally end up with a single resistance. So, to calculate the resistance we just have to solve "cases" of series and parallel like we described before, remembering the two basic rules:
- Same current flow through series resistors
- Same voltage across parallel resistors
[2][3][4] (for all the combination section)
How to solve problems around Resistors
So, which exact steps are the best to take to solve the simple and more complex cases?
Well, it depends on the problem and from what I understand it clearly depends a lot on what we actually want to calculate. Most of the times what we want to calculate is not the total resistance of the whole complex circuit, but just a current, voltage or resistance of a specific point on the circuit.
Just always remember the following tips:
- Understand the connections and how the physics quantities that we study change depending on those combinations. This means that you should always know how to calculate the voltage (potential difference), current and resistance for any case.
- In series we have the same current and the voltage is the sum of each individual voltage drop.
- In parallel we have the same voltage and the current is the sum of each individual current.
- From the last two tips you can see that the current-voltage relationship if different depending on the combination and you should never, ever confuse them.
- A good way of solving complex circuits is by trying to solve parallel branches to turn them into serial ones. When having something serial in the parallel combation we of course will have to solve this serial connection first, but the main focus should always be solving the parallel ones. Having all the parallel connections solved the final step is solving a single serial connection then the total resistance is just a sum of each individual one.
Tips are based on what I know and learned about them in total...
Examples for all this can be found in the following links:
- http://www.physicsclassroom.com/class/circuits/Lesson-4/Combination-Circuits
- https://www.electronics-tutorials.ws/resistor/res_5.html
- http://www.dnatechindia.com/Resistor-Combinations.html
- https://www.electronicshub.org/resistors-in-series-and-parallel-combinations/
REFERENCES:
To refresh my knowledge I used a lot of the following:
- https://en.wikipedia.org/wiki/Resistor
- http://www.physicsclassroom.com/class/circuits/Lesson-4/Combination-Circuits
- https://www.electronicshub.org/resistors-in-series-and-parallel-combinations/
- https://opentextbc.ca/physicstestbook2/chapter/resistors-in-series-and-parallel/
Some mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
And this is actually it for today's post and I hope that you enjoyed it!
Next time we will cover Kirchoff's laws!
See ya!
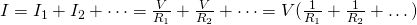
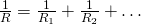
Hi @drifter1!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Resistors are passive circuit elements i. e they cannot amplify an electrical signal. Obviously from the name, they offer opposition to the flow of current be it in an AC or DC circuit. I remember having to question the use of resistors in an electronic circuit while in secondary school. My teacher fail to explain it to us.
But what is their importance in a circuit? It is to control the flow of current to other components and in a way acting as "current regulator".
Despite being one of the cheapest electronic component, it cannot be overlooked as less important in a circuit.
Congratulations @drifter1! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard!
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes