Criterios de Estabilidad de Sistemas Materiales en Estática Aplicada

Saludos y bienvenidos, en esta oportunidad aprenderemos un poco sobre los criterios de estabilidad de los sistemas materiales, tema fundamental en el estudio de la estática aplicada a la Ingeniería Civil. Para el estudio de la estabilidad es importante que el estudiante/lector aprenda algunos criterios básicos para reconocer cuándo y cómo se da. Esta lectura es la continuación de los siguientes artículos:

• Introducción al Estudio de la Estática Aplicada

• Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad

• Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación

Con esta publicación se busca dejar expresado de una manera concisa y didáctica el análisis de estabilidad de sistemas materiales de acuerdo al criterio del número de grados de libertad que los mismos poseen. Para el estudiante de Ingeniería Civil es muy importante reconocer cuando un sistema estructural es estable o no, o si tiene más vinculaciones de las necesarias para que el sistema sea estable. Por ello, también se estudian los sistemas inestables, que tienen la posibilidad de presentar movimiento para así poder diferenciarlos respecto de los sistemas estables, los cuales son de principal interés en el estudio de la Estática Aplicada.

---

Criterios de Estabilidad

Los grados de libertad son una medida de que tan inestable es un sistema material. Un sistema material que presenta la posibilidad de moverse total o parcialmente (es decir por lo mínimo uno de sus elementos tiene la libertad de moverse sin restricción) debe tener por lo menos, un grado de libertad, en otras palabras este sistema es inestable. Si el sistema material presenta las vinculaciones mínimas suficientes para que todos los movimientos de sus puntos se restrinjan totalmente, entonces el sistema está en equilibrio estático (isostático) y tiene cero grados de libertad. Si existen más vinculaciones de las necesarias para que el sistema material sea estable, entonces se dice que el mismo es hiperestático, y los grados de libertad resultan en un número negativo. Recordemos que los grados de libertad se calculan multiplicando por tres el número de chapas y restando las unidades de vinculación tanto externas como internas que posee el sistema material (ver Referencia [5]).

Vemos entonces como podemos clasificar los sistemas materiales según los grados de libertad que estos poseen. Cabe destacar que cada uno de estos criterios se cumple solo bajo ciertas condiciones. Según González-Cuevas (2002): “La inestabilidad se deriva de un número insuficiente o de una disposición inadecuada de los apoyos, o bien, de un arreglo inadecuado de partes de la estructura”. (p. 34). También señala González-Cuevas que cuando hay una disposición inadecuada de los apoyos o un arreglo inadecuado de partes de la estructura, la inestabilidad es geométrica. Esto quiere decir que un sistema material puede tener el número de vinculaciones suficientes para ser isostático (cero grados de libertad), o incluso clasificarse como hiperestático, pero si existe mala disposición de vínculos el sistema podría presentar movimiento y de esta manera sería inestable. Si esto ocurre, estaríamos en presencia de vínculos que no añaden o introducen ninguna unidad de vinculación debido a su posición o ubicación, es decir, vínculos aparentes [3].

Todo esto nos lleva a decir lo siguiente: para que un sistema sea estable, la condición GL=0 es necesaria, pero al mismo tiempo no es suficiente [3]. La estabilidad se verifica si se cumple la condición de suficiencia, es decir, al comprobar que no existen vinculaciones mal dispuestas (aparentes) que no aportan restricción al sistema.

---

Sistemas Inestables (Hipostáticos)

Cuando el número de grados de libertad es mayor o igual a la unidad, se dice que el sistema material es inestable o hipostático. Al ser sistemas que presentan movimiento, se les suele llamar “mecanismos”.

Un sistema puede presentar inestabilidad general, que es cuando no existe el número de vinculaciones suficientes para que el sistema sea estable.

_{Figura N°1: el sistema mostrado presenta tres grados de libertad según la Ecuación (1), es decir, existen tres parámetros independientes (desplazamientos y/o rotaciones) con los cuales se puede describir el movimiento del sistema material. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

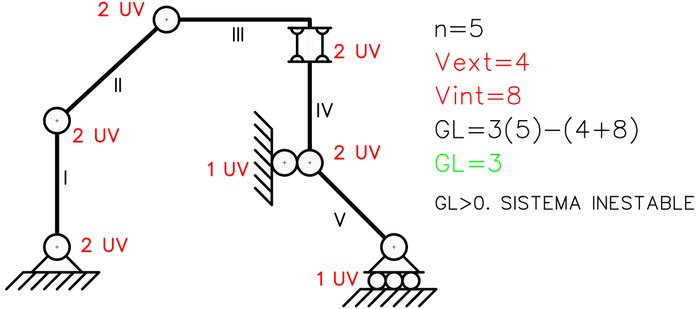
Recordemos la ecuación utilizada para calcular los grados de libertad de un sistema material (Referencia [5]):

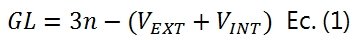
Sin embargo, puede que exista el número suficiente de vinculaciones pero al estar mal dispuestas se genera inestabilidad. Esta situación se conoce como inestabilidad geométrica y pueden presentarse tanto externa como internamente.

_{Figura N°2: par de ejemplos de inestabilidad geométrica externa. Primero vemos una chapa con tres restricciones paralelas, esto genera que la chapa pueda desplazarse en la dirección perpendicular, además se dice que uno de los tres apoyos simples es aparente ya que no aporta restricción adicional al sistema. Luego vemos un ejemplo de restricciones concurrentes en un punto, donde se genera un centro de rotación (polo) sobre el cual la chapa tiene la libertad de girar. De nuevo se dice que uno de los apoyos (cualquiera) es aparente, ya que no evita la rotación y puede removerse sin alterar la movilidad del sistema. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

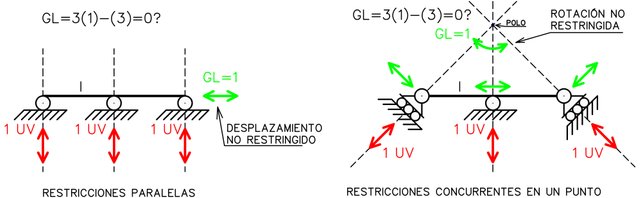
Se genera inestabilidad geométrica externa cuando existen suficientes vinculaciones externas para generar estabilidad pero el sistema tiene la posibilidad de presentar movimiento respecto al sistema tierra.

_{Figura N°3: el sistema presentado posee vinculaciones de sobra para poder ser estable (número negativo de grados de libertad) pero la mala disposición de las vinculaciones externas (apoyos) hace que el sistema material pueda moverse respecto al sistema tierra. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

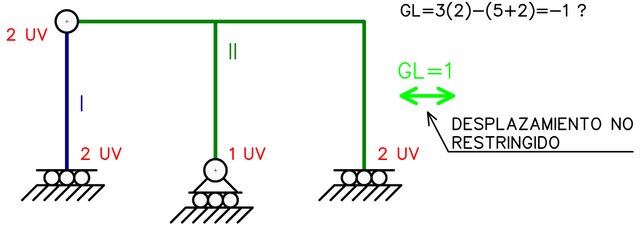
Por otro lado, si internamente existe la posibilidad de presentarse movimiento relativo de un cuerpo respecto a otro, la inestabilidad geométrica es interna.

_{Figura N°4: a pesar de que sobran dos vinculaciones y las vinculaciones externas estar bien dispuestas, internamente hay inestabilidad debido al mal arreglo de partes de la estructura. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

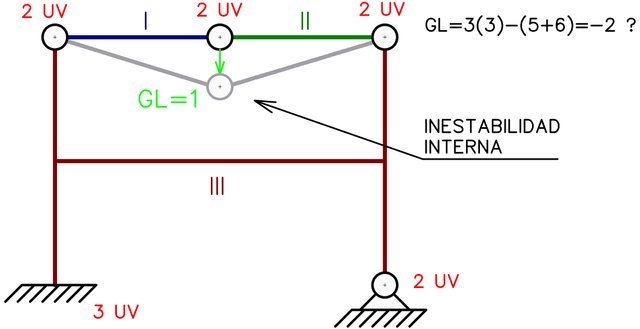
Recordemos que en el estudio de sistemas materiales en estática aplicada, las rotaciones que se pueden presentar son de orden infinitesimal, generando desplazamientos muy pequeños en comparación a las dimensiones de los elementos [4]. Por ello en la Figura N°4, el arreglo interno de dos barras articuladas que están alineadas entre sí con sus extremos opuestos fijos, genera una inestabilidad que permite a ambas barras presentar una rotación infinitésima con un pequeño desplazamiento en la rótula (en verde). Este desplazamiento es tan pequeño, que podemos asumir que cada barra no cambia de longitud al presentarse el movimiento.

---

Sistemas Isostáticos

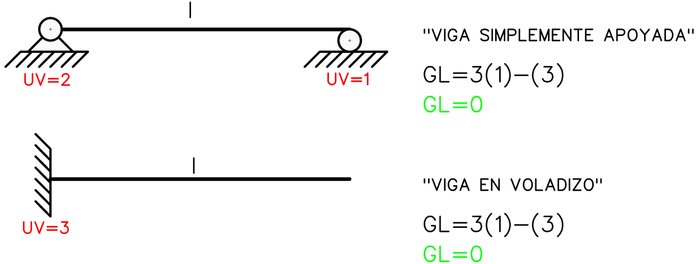
Cuando se comprueba que no hay vínculos mal dispuestos en el sistema material y además se tiene que GL=0, entonces el sistema es estable. Este sistema posee las mínimas vinculaciones necesarias para garantizar que no se produzca movimiento alguno en el mismo. El prefijo “iso” denota que todo el sistema material se encuentra bajo el mismo estado de equilibrio estático, es decir, no hay inestabilidades parciales ni vínculos de sobra para garantizar la estabilidad. Un ejemplo “elemental” de un sistema material isostático es la “viga simplemente apoyada”, también lo puede ser un elemento empotrado a tierra en un extremo.

_{Figura N°5: dos ejemplos simples de sistemas isostáticos: la “viga simplemente apoyada” y la viga en “voladizo”. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

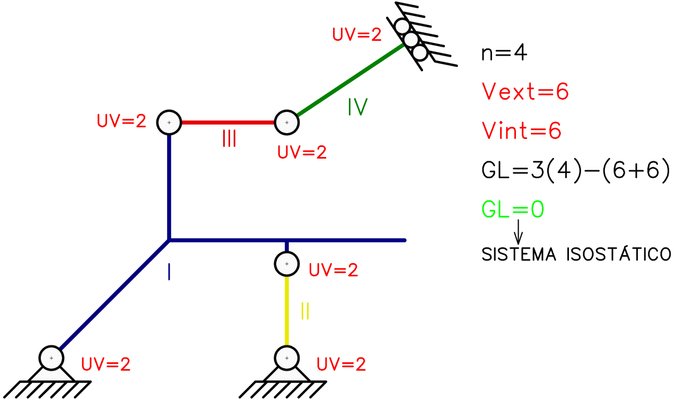
Un sistema material más complejo y de igual manera isostático es como el que se muestra en la Fig. N°6.

_{Figura N°6: sistema material isostático. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

---

Sistemas Hiperestáticos

Cuando se tiene un número negativo de grados de libertad, el sistema presenta hiperestaticidad. El prefijo “hiper” denota que existen vinculaciones en exceso, más de las necesarias para garantizar el equilibrio estático. Esto nos lleva a una nueva caracterización, los vínculos superabundantes, que se definen según Hernández (1998) como: “Vínculos adicionales al número mínimo que se requiere para llevar a condiciones de equilibrio un mecanismo cinemático”. (p. 10).

Si se cumple que no existen vinculaciones mal dispuestas (aparentes), entonces se puede establecer la siguiente relación:

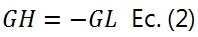
Donde “GH” representa a los grados de hiperestaticidad. De esta manera, los grados de hiperestaticidad indican cuantas vinculaciones superabundantes existen en el sistema material. Estos sistemas son objeto de estudio en temas más avanzados de análisis estructural puesto que pueden representar de forma idealizada estructuras reales las cuales en muchos casos son hiperestáticas. En estática aplicada se analizan estos sistemas únicamente desde el punto de vista del análisis de la estabilidad. En la Figura N°7 un ejemplo de sistema material hiperestático.

_{Figura N°7: el sistema material presenta dos grados de hiperestaticidad, es decir, posee dos vinculaciones superabundantes. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

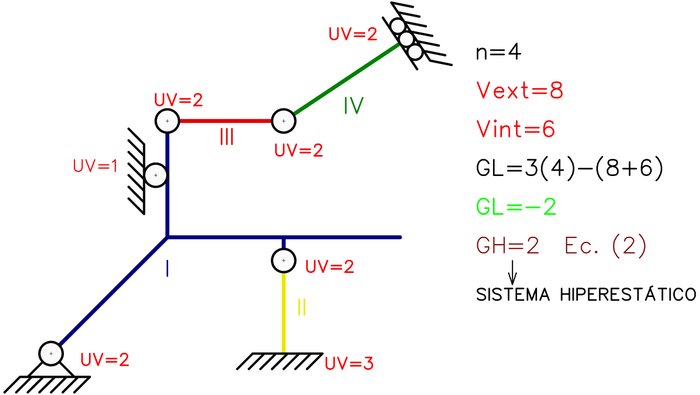
No obstante, podemos observar que respecto a la Figura N°6 hemos agregado dos unidades de vinculación al sistema (un apoyo simple de rodillo y se restringió la rotación de una de las articulaciones a tierra), haciendo que el sistema tenga más vinculaciones de las necesarias para que sea estable respecto al sistema tierra. Sin embargo, también puede darse el caso de que internamente una chapa compuesta por varias barras tenga más vinculaciones internas de las necesarias para que pueda considerarse cuerpo rígido plano. Esto significa que un sistema material puede ser isostático externamente pero presentar hiperestaticidad interna, como es el caso de la Figura N°8.

_{Figura N°8: a la izquierda se consideró todo el conjunto de barras como un solo cuerpo rígido ya que no presenta deformabilidad, de esta manera se comprueba mediante el cálculo de los grados de libertad que externamente no presenta hiperestaticidad. A la derecha se consideró cada barra como cuerpo rígido individual y se determinó que internamente existe hiperestaticidad de segundo grado, es decir, internamente hay dos vinculaciones además de las necesarias para que el sistema material presente estabilidad interna. Para tres barras vinculadas por junta rígida se usó la ecuación UV=3(n-1) [4], donde “n” representa el numero de barras. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

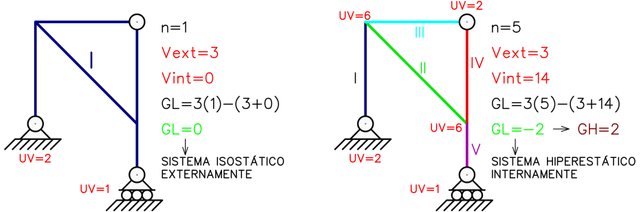
De esta manera podemos llegar al siguiente criterio para el estudio de la hiperestaticidad de sistemas materiales: si consideramos a cada chapa como el mayor número de elementos que vinculados entre sí logra conformar un cuerpo rígido entonces estamos estudiando la hiperestaticidad externa, en cambio si consideramos a cada barra como una chapa por separado y tomamos en cuenta el efecto de cada una de las juntas rígidas estamos estudiando la hiperestaticidad interna. Puede darse el caso de que un sistema material sea isostático o incluso inestable externamente pero presentar hiperestaticidad interna.

---

En resumen, un sistema material puede ser estable o inestable, de acuerdo a varios criterios según vemos en la Figura N°9.

_{Figura N°9: lo sistemas materiales estables son isostáticos o hiperestáticos, mientras que los inestables son mecanismos que no poseen las vinculaciones suficientes para ser estables o que si las poseen pero están mal dispuestas. | Imagen elaborada mediante LibreCAD | @acont | 2018.}

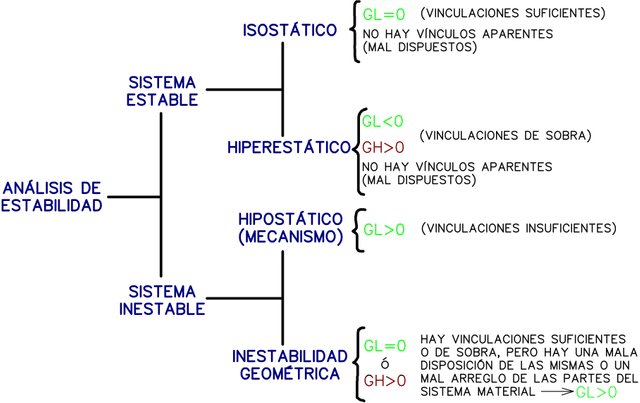
El análisis de estabilidad de sistemas materiales también puede realizarse tanto externa como internamente. La inestabilidad geométrica puede presentarse externamente cuando el sistema material puede considerarse como un cuerpo rígido en su totalidad pero la mala disposición de vinculaciones externas genera posible movimiento respecto al sistema tierra, o internamente cuando un mal arreglo de partes del sistema o mala disposición de un vínculo interno genera posible movimiento relativo entre chapas. De igual manera la hiperestaticidad puede ser externa cuando existen vínculos externos de sobra para garantizar el equilibrio estático, o interna cuando un arreglo de barras presenta más vinculaciones internas de las necesarias para considerar este arreglo un cuerpo rígido plano (chapa).

En algunas ocasiones, reconocer cuando una vinculación es aparente no es tan evidente, por ello en futuras publicaciones estudiaremos técnicas que nos ayudan a verificar la estabilidad de un sistema material, ya que la condición “GL=0” es necesaria pero no suficiente, y debemos estar seguros de poder cumplir de manera satisfactoria la condición de suficiencia. De igual manera abordaremos métodos que nos ayudan a calcular la hiperestaticidad interna de un sistema material de una manera más práctica.

---

Referencias

[1] Hernández, Suilio. (1998). Estática Aplicada. Caracas, Venezuela: Folleto Editado por el Departamento de Ingeniería Estructural U.C.V.
[2] González C. Oscar M. (2003). Análisis Estructural. México: Universidad Autónoma Metropolitana. LIMUSA.
[3] @acont. Introducción al Estudio de la Estática Aplicada. Disponible en: https://steemit.com/stem-espanol/@acont/introduccion-al-estudio-de-la-estatica-aplicada
[4] @acont. Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad. Disponible en: https://steemit.com/stem-espanol/@acont/estatica-aplicada-los-vinculos-y-su-aplicacion-a-sistemas-estructurales-en-la-realidad
[5] @acont. Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación. Disponible en: https://steemit.com/stem-espanol/@acont/determinacin-algebraica-de-los-grados-de-libertad-de-sistemas-materiales-en-esttica-aplicada-y-ejemplo-de-aplicacin-1540254330

---

Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word por @acont. Otras imágenes presentan su fuente respectiva.

---

Para encontrar contenido relacionado con Ciencia, Tecnología, Ingeniería y Matemáticas visite las etiquetas #steemstem y #stem-espanol. @STEM-espanol es una subcomunidad de @SteemSTEM que apoya y promueve el contenido académico-científico de alta calidad de la comunidad hispanohablante, puedes aprender más de ella uniéndote a su canal de Discord.