Introducción a las Ecuaciones Diferenciales Ordinarias | Lección #6

Saludos queridos lectores, bienvenidos nuevamente. Este post es la 6ta entrega de la serie Introducción a las Ecuaciones Diferenciales, en está oportunidad abordaremos el estudio de las ecuaciones diferenciales ordinarias de segundo homogénea con coeficientes constantes, su planteamiento y como llegar a su resolución. La misma está dirigida al público en general, pero con atención especial a estudiantes universitarios de ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Ecuaciones Diferenciales Ordinarias de 2do orden Homogénea con Coeficientes Constantes

En esta oportunidad abordaremos la resolución de Ecuaciones Diferenciales Ordinarias de 2do orden, homogéneas con coeficientes constantes, aquí estableceremos su método de resolución así como resolveremos algunos ejercicios.

---

Una ecuación diferencial de 2do segundo orden, homogénea con coeficientes constantes es de la forma siguiente:

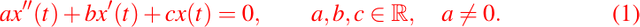
La ecuación dada por (1) lo que nos dice es que una cierta combinación lineal de x(t), x'(t) y x''(t), se anula.

Si usamos un poco de cálculo diferencial elemental, podemos verificar que:

es una candidata a ser solución del problema dado en (1) para un cierto valor de r. Luego, derivando esta posible solución y sustituyendo en la ecuación (1) se obtiene:


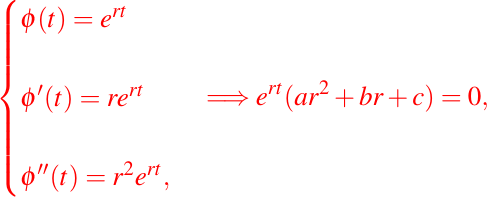
Si es una candidata a ser solución de la ecuación dada por (1), y ademas como el producto de esos dos factores es cero, entonces tenemos que:


A la ecuación (2) se le conoce como la ecuación característica de (1). Sus raíces están dadas por:


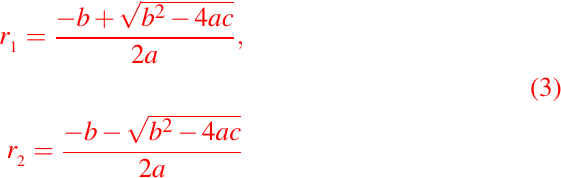
lo cuál nos lleva a estudiar los distintos casos.

---

---

Caso #1:

---

En este caso, sabemos que las raíces de la ecuación característica dada por (2) son reales y distintas, es decir,

son dos soluciones de la ecuación diferencial ordinaria dada en (1), donde las raíces están dadas por:


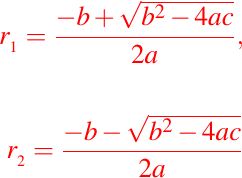
Además,


Entonces


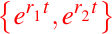
es base de soluciones de (1) y toda solución de la ecuación dada en (1) es de la forma:

---

---

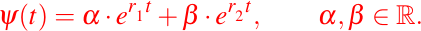
Caso #2:

---

En este caso, la ecuación característica dada por (2) tiene dos raíces iguales, a saber:

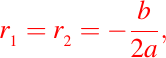
para lo cuál tenemos entonces solo una solución de la ecuación descrita por (1); como sigue:


La segunda solución tal que formemos una base de soluciones de la ecuación dada en (1), la podemos hallar aplicando el método de reducción de orden visto en la Lección #5, así de acuerdo con dicho método, debemos encontrar una solución tal que:


sea también una solución. Entonces, como ya vimos en la Lección #5, anterior,


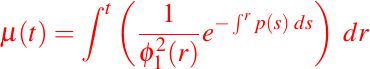
En nuestro caso,


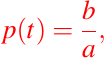
Así, tenemos entonces que:


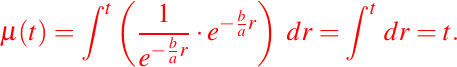
Entonces


Por lo tanto, el conjunto formado por:


es una base de soluciones de la ecuación dada por (1) y todas las soluciones vienen dadas de la forma:


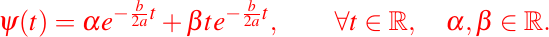
Observemos que en este caso, toda solución de la forma anterior de la ecuación (1) tenemos que:

---

---

Caso #3:

---

En este caso, las raíces de la ecuación característica dada por (2) son dos raíces complejas conjugadas, a saber;

Para poder continuar necesitamos el siguiente lema:


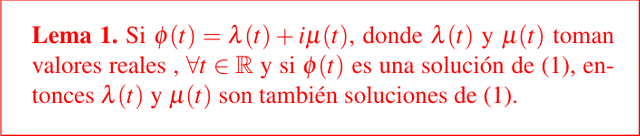
Para una demostración puede consultar

• Boyce, William E., Richard C. DiPrima, and Charles W. Haines. Elementary differential equations and boundary value problems. Vol. 9. New York: Wiley, 1969.

Ahora, regresando a nuestro caso, tenemos que

es una solución de (1) y por el lema enunciado anteriormente tenemos:


son soluciones reales de (1).

Como

entonces por el teorema de la Lección #5, la ecuación dada por (4) es una base de soluciones de (1) y la solución general esta dada por:

---

---

Ejemplo 01: Demuestre que cada solución no cero de


se anula a lo más una vez en los números reales.

---

La ecuación característica de la ecuación dada es

donde las raíces son


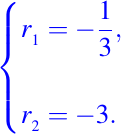
Luego, una base de soluciones para la ecuación dada es:


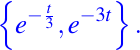
La solución general esta dada por:


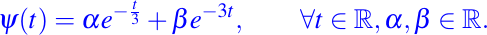
Así, la solución no es la solución cero, ella se anula a lo más una vez, y si lo hace, la hace para t=0.

---

---

Ejemplo 02: Demuestre que si


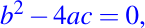
entonces toda solución de


es acotada en los reales positivos.

---

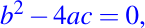
Como lo acotamos anteriormente, si dada una solución de la ecuación anterior, entonces

Luego, hay valor M positivo tal que


Pero como esta solución es continua en los números reales, en particular es continua en [0,M], y por el hecho que [0,M] es compacto, entonces esta solución es acotada en [0,M].

Sea L un número real positivo tal que

Si

entonces

---

---

Ejemplo 03: Si las raíces de la ecuación característica dada por la ecuación (1) tienen parte real negativa, entonces


para toda solución de la ecuación (1).

---

En efecto, si la parte imaginaria de dichas raíces es cero, entonces nuestro problema se reduce al Caso #1, que ya vimos anterioremente entonces toda solución es de la forma

y como por hipótesis tenemos que:


de donde

Si tenemos que 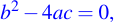entonces tenemos que:

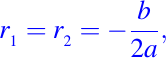
como lo vimos ya anteriormente en el Caso #2, luego por la hipótesis, implica que el valor debe ser mayor que cero. aplicando la reglas de L'Hôpital, tenemos:


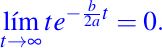
y como lo vimos en el Caso #2, toda solución de (1) es de la forma siguiente:


Luego,

Si finalmente la parte imaginaria de las raíces de la ecuación característica es distinta de cero, entonces por la ecuación dada en (5) y también porque

son funciones acotadas en los números reales, se tiene que

---

---

Queridos amigos y lectores, espero hayan disfrutado de esta 6ta entrega de la serie de Introducción a las Ecuaciones Diferenciales, de igual manera los invito para la próxima entrega de esta serie, donde continuaremos tratando este tema tan interesante e importante y de mucha aplicación en la ciencia e ingeniería. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y sus aplicaciones. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias.

• Beléndez, Augusto. Ecuaciones diferenciales ordinarias. Métodos Matemáticos de la Física. 1987.
• Hartman, Philip. Ordinary differential equations. (2002).
• Coddington, Earl A., and Norman Levinson. Theory of ordinary differential equations. McGraw-Hill Education, 1955.
• Boyce, William E., Richard C. DiPrima, and Charles W. Haines. Elementary differential equations and boundary value problems. Vol. 9. New York: Wiley, 1969.

---

También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales, que estoy seguro serán de su interés:

Lección #1	Lección #2	Lección #3	Lección #4	Lección #5

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath con
, y GIMP.

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}