Saludos queridos lectores, bienvenidos nuevamente. Este post es la cuarta entrega de la serie Introducción a las Ecuaciones Diferenciales, en está oportunidad abordaremos el estudio de las ecuaciones diferenciales ordinarias de segundo, su planteamiento y como llegar a su resolución. La misma está dirigida al público en general, pero con atención especial a estudiantes universitarios de ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Ecuaciones Diferenciales Ordinarias de 2do Orden

En este post empezaremos a estudiar las ecuaciones diferenciales ordinarias de 2do orden, comenzaremos hablando del espacio de soluciones y el Wronskiano, los cuales describiremos a continuación.

Espacios de soluciones y el Wronskiano

Para ellos debemos definir una ecuación diferencial ordinaria de 2do orden de forma general, de la siguiente manera:

Sean

tres funciones continuas. Entonces la ecuación diferencial ordinaria siguiente


se le conoce como una ecuación diferencial ordinaria lineal de segundo orden normalizada general.

Cuando decimos normalizada nos referimos a que el coeficiente de la segunda derivada es idénticamente 1 en (a,b). Ahora si g es idénticamente cero en (a,b), entonces la ecuación descrita en (1) toma la forma:

y se le conoce como la ecuación diferencial ordinaria lineal de segundo orden homogénea normalizada.

Para poder desarrollar los conceptos de este post debemos enunciar unos resultados previos los cuales no presentaremos su demostración, pero colocaremos una referencia donde el lector puede consultar su demostración con detalles. El único resultado que demostraremos es el referente al teorema 3, el cuál tiene implicación directa en este post.

Ahora con respecto a la ecuación dada en (2) tenemos el siguiente teorema:

Para una demostración pueden consultar la siguiente referencia:

• Boyce, William E., Richard C. DiPrima, and Charles W. Haines. Elementary differential equations and boundary value problems. Vol. 9. New York: Wiley, 1969.

---

---

Ahora definamos el Wronskiano como sigue:

---

---

A continuación enunciaremos el siguiente teorema y daremos una demostración del mismo, para mostrar las equivalencias de cuando dos soluciones son linealmente independientes:

Demostración:

. Evidente.

. Supongamos que

no forman una base de soluciones de (2), entonces por el teorema (2), el conjunto anterior no es linealmente independiente, así existen dos escalares, digamos


de tal manera que se satisface lo siguiente por la definición de funciones linealmente dependientes:


en consecuencia, derivando la ecuación anterior con respecto a la variable t, obtenemos:


luego, de estas dos últimas igualdades deducimos que el sistema lineal dado a continuación


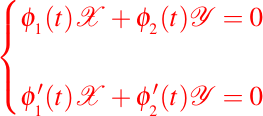
tiene la solución no trivial, a saber:


Por lo tanto, se tiene

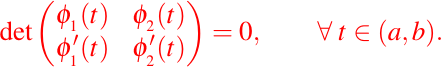
En otras palabras, tenemos que:


lo cual contradice nuestra hipótesis (2), así la suposición que hicimos al principio es falsa, por lo tanto hemos probado la implicación.

. Demostremos por reducción el absurdo, es decir, supongamos que (1) es falso. Así, existe,

por lo tanto


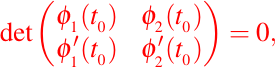
de esta manera, el sistema lineal siguiente:


tiene una solución no trivial, es decir, existen dos escalares, digamos


tal que podemos definir, la siguiente función de la forma:


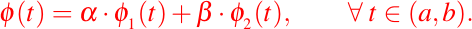
así, la función que acabamos de definir es solución de (2), ya que satisface las condiciones iniciales, pero la solución nula también satisface las mismas condiciones iniciales. En consecuencia,


lo cual contradice que las dos funciones son linealmente independientes. De esta manera, por reducción al absurdo (1) es cierto.

---

Lo cual completa la prueba de las equivalencias de las tres proposiciones. Pasemos a mostrar un ejemplo donde aplicamos el teorema.

---

---

Ejemplo: Mostrar que las funciones siguientes son linealmente independientes

En efecto, estas funciones son linealmente independientes en el intervalo abierto (-1,1), ya que ninguna es un múltiplo escalar de la otra, sin embargo se tiene que

)
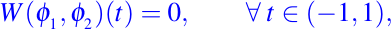Entonces por el teorema anterior, deducimos que las funciones no pueden ser solución de una ecuación diferencial ordinaria como la dada en (2).

Aprovechemos la oportunidad de observar que aunque las funciones son linealmente independientes en (-1 , 1), ellas son linealmente dependientes en el subintervalo (0,1) de (-1 , 1), sobre el conjunto de los números reales.

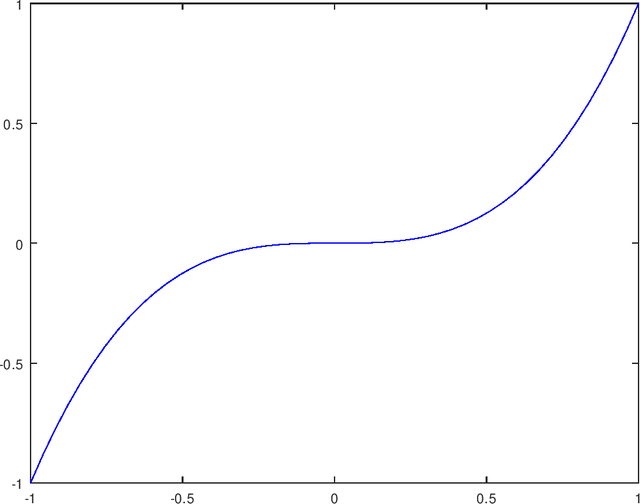
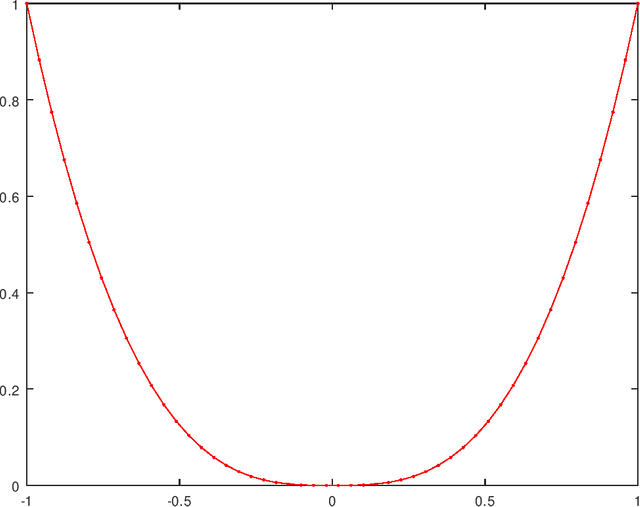
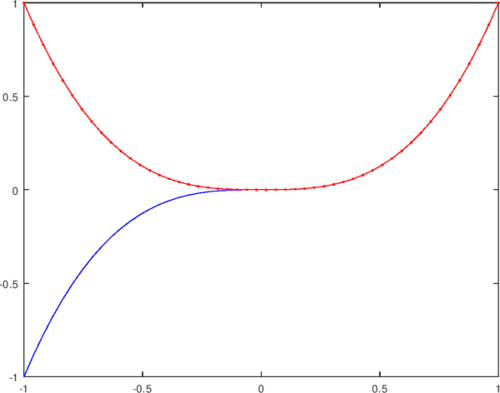
Lo cuál podemos apreciar al realizar el estudio de las gráficas siguientes. Las dos primeras, son las funciones graficadas por separados, y la última podemos apreciar que el intervalo (0,1) las dos funciones se superponen una sobre la otra, es por ellos que las dos funciones son linealmente dependientes en el intervalo (0,1).

---

---

Queridos amigos y lectores, espero hayan disfrutado de esta tercera entrega de la serie de Introducción a las Ecuaciones Diferenciales, de igual manera los invito para la próxima entrega de esta serie, donde continuaremos tratando este tema tan interesante e importante y de mucha aplicación en la ciencia e ingeniería. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y sus aplicaciones. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias.

• Beléndez, Augusto. Ecuaciones diferenciales ordinarias. Métodos Matemáticos de la Física. 1987.
• Hartman, Philip. Ordinary differential equations. (2002).
• Coddington, Earl A., and Norman Levinson. Theory of ordinary differential equations. McGraw-Hill Education, 1955.

---

También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales, que estoy seguro serán de su interés:

Lección #1	Lección #2	Lección #3

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath con
, y GIMP.

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}