Saludos queridos lectores, bienvenidos nuevamente. En este post desarrollaremos una serie llamada Introducción a las Ecuaciones Diferenciales, donde abordaremos su planteamiento y como llegar a su resolución. La misma está dirigida al público en general, pero con atención especial a estudiantes universitarios de ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Introducción a las Ecuaciones Diferenciales Ordinarias

A manera de introducción, o explicación breve, sabes que las reglas o leyes que rigen el universo siempre las podemos describir en función del lenguaje de las matemáticas. Por ejemplo, si queremos resolver problemas que no dependan del tiempo, es decir, estacionarios, mucha veces es suficiente con usa el álgebra. Pero en la mayor parte de los casos, los fenómenos naturales o físicos que son de interés dependen del tiempo, es decir, las ecuaciones que los describen involucran cantidades de cambio, lo cual lo relacionamos con una variable del tiempo t, la cual es independiente.

Ahora bien muchas de estás ecuaciones que involucran cambios, están definidas a partir de una función que desconocemos su descripción analítica, y como sabemos funciones las funciones que describen cambios estan relacionadas con la derivada de alguna función, valga la redundancia, en otras palabras a este tipo de ecuaciones que involucran derivadas de funciones desconocidas muchas veces, se les denomina Ecuaciones Diferenciales.

Las Ecuaciones Diferenciales, formal parte del papel fundamental en muchas de las disciplinas, tales como: la ingeniería, la física, la economía, la biología, la química, entre otras más.

---

---

Ecuaciones Diferenciales Ordinarias Lineales de 1er Orden

Definamos una ecuación diferencial de 1er orden de manera general.

Sean

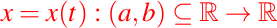
y

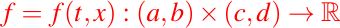
dos funciones, donde x(t) es una función diferenciable y f(t,x) es una función continua, entonces a la ecuación

se le conoce como una ecuación diferencial de primer orden . Si ahora tenemos una función, digamos

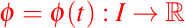
la llamaremos una solución local de (1) si

donde I, es un subintervalo no degenerado.

Ahora bien, si el gráfico de la solución local, pasa por el punto dado; es decir, si

entonces decimos que la función satisface la condición inicial.

de esta manera (1) y (2) constituyen lo que se conoce como un problema con valores iniciales.

---

Si a la ecuación (1) la podemos escribir de la siguiente manera:

decimos es que es: la ecuación diferencial lineal de primer orden normalizada, donde p(t) y g(t) son funciones continuas. El nombre de normalizada se debe a que el coeficiente de la derivada es idénticamente 1. En el caso que g=g(t) sea idénticamente cero en (a,b), entonces a la ecuación (3) se le conoce como ecuación diferencial lineal de 1er orden homogénea.

La ecuación diferencial lineal de 1er orden homogénea más simple es:

si multiplicando (4) por

tenemos

podemos observar entonces lo siguiente

de donde tenemos que

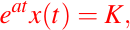
con K una constante.
Luego despejando x(t) obtenemos:

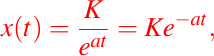
Es fácil verificar que está es solución de (4). Así, todas las soluciones de (4) son de esa forma con K una constante. Ahora, si especificamos una condición inicial (2), el problema con valores iniciales (4), (2), tiene una solución única, a saber:

---

---

Ahora, queremos resolver la ecuación diferencial lineal de 1er orden normalizada (1). Para ellos, motivados en la forma que acabamos de hacer para resolver nuestro caso simple, entonces debemos encontrar una función

tal que:

a esta función se le conoce como un factor de integración (3). Ahora, como

entonces debe satisfacer

sin perdida de generalidad, supongamos por un momento que el factor de integración sea positivo y distinto de cero en I. Entonces, para obtener (5) es suficiente tener:

es decir,

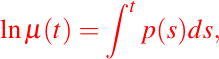
despejando tenemos:

multipliquemos ahora (3) por el la función dada en (6), entonces se tiene:

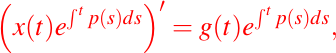
así, integrando ambos miembros de la igualdad anterior, obtenemos:

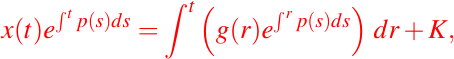
donde K es constante, por lo tanto,

Es fácil verificar haciendo uso del Teorema Fundamental del Cálculo, que cualquier función dada por (7), y para cualquier constante K, son soluciones de la ecuación (3).

Usando la notación referida en (6), la solución general dada por la ecuación (7) del problema (3) toma la forma;

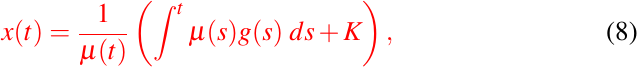
Luego, si se da una condición inicial, K queda únicamente determinada y así el problema (3), (2) tiene una única solución.

---

---

A continuación, presentaremos un ejemplo de como usar lo que hemos visto para resolver una ecuación diferencial ordinaria lineal de 1er orden.

Ejemplo: Resolver el problema con valores iniciales

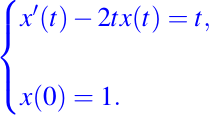
Para resolver el problema con valores iniciales, primeramente usemos la ecuación dada en (6) para así conseguir la función factor de integración la cual para este caso es:

Adicionalmente se tiene lo siguiente:

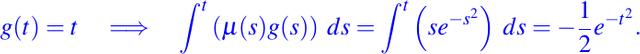
Luego, usando la ecuación de la solución dada por (8) tenemos que la solución general al problema con valores iniciales planteado es:

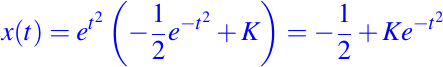
usando la condición inicial dada tenemos:

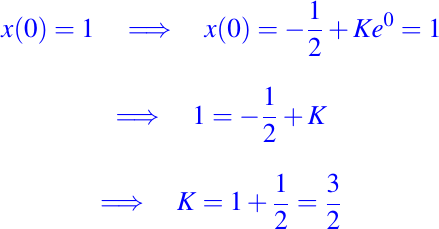
Entonces, la solución única del problema con valores iniciales dado es

---

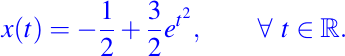
Queridos amigos y lectores, espero hayan disfrutado de esta primera entrega de la serie de Introducción a las Ecuaciones Diferenciales, de igual manera los invito para la próxima entrega de esta serie, donde continuaremos tratando este tema tan interesante y de mucha aplicación. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la computación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias.

• Beléndez, Augusto. Ecuaciones diferenciales ordinarias. Métodos Matemáticos de la Física. 1987.
• Hartman, Philip. Ordinary differential equations. (2002).
• Coddington, Earl A., and Norman Levinson. Theory of ordinary differential equations. McGraw-Hill Education, 1955.

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath con , y GIMP.

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}