Saludos queridos lectores, bienvenidos nuevamente. Este post es la 8va entrega de la serie Introducción a las Ecuaciones Diferenciales, en está oportunidad abordaremos el estudio de algunas aplicaciones de las ecuaciones diferenciales ordinarias, en esta publicación trataremos aplicaciones en diversas áreas, como química, economía, física, entre otras. Se tratará de hacerlo de una forma didáctica sin perder de vista el formalismo matemático, en cada aplicación daremos un pequeña descripción del proceso y de como deducir la forma de abordar el problema y seguidamente un ejemplo. La misma está dirigida al público en general, pero con atención especial a estudiantes universitarios de ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Aplicaciones de las Ecuaciones Diferenciales Ordinarias

Como ya lo habíamos comentado en la 1era publicación de esta serie, Introducción a las Ecuaciones Diferenciales Ordinarias | Lección #1

Las Ecuaciones Diferenciales, forman parte del papel fundamental en muchas de las disciplinas, tales como: la ingeniería, la física, la economía, la biología, la química, entre otras más.

La gran parte de los problemas significativos e importantes, que se formulan en términos de las matemáticas, siempre están necesitan de encontrar una cierta función que bajo ciertas condiciones satisface una ecuación, donde dicha ecuación contiene términos de derivadas de esa función que se desconoce. Esas ecuaciones son las Ecuaciones Diferenciales.

Si debemos hablar de algunos ejemplos, no podemos dejar de mencionar el mas conocido o el ejemplo clásico de la física, como es la Ley de Newton:

donde m la masa de una partícula, u(t) es la función desconocida que describe la posición de una partícula, sobre la cual actúa una fuerza F, que depende del tiempo, de la posición de la partícula en un instante de tiempo y de la velocidad de la partícula. Si deseamos determinar el movimiento de la partícula, entonces es necesario determinar la función u(t) que satisface la ecuación (1).

Si ahora decimos que la fuerza que actúa sobre el sistema físico descrito en (1), es la gravedad, entonces podemos escribir la ecuación de la forma siguiente:

ahora, como la masa y la gravedad no depende de el tiempo t, y la masa es una cantidad distinta de cero, entonces podemos integrar dos veces con respecto al tiempo, y así obtenemos lo ecuación que mostramos a continuación:

donde K₁ y K₂ son constantes reales. La ecuación mostrada en (3) es la solución general de la ecuación (2), ahora si queremos determinar la solución completamente se necesitan especificar las condiciones, es decir, la posición y la velocidad de la partícula en algún instante de tiempo, con ellos podríamos determinar los valores de las constantes K₁ y K₂ para dar la solución única del problema planteado.

Un segundo ejemplo, que es bueno mencionar es el de los circuitos eléctricos en serie, cuya ecuación esta basado en la 2da Ley de Kirchhoff :

donde, Q(t) es la carga del condensador de un circuito en serie cerrado, C la capacitancia, R la resistencia, L la inductancia, y E(t) el voltaje aplicado.

Otro ejemplo, es el que trata del calculo de cierta cantidad R(t) de una substancia radiactiva, donde se modela como decae el radio en función del tiempo, como sigue:

donde k es una constante conocida, llamada constante de proporcionalidad, donde dependiendo del signo puede tener diferentes interpretaciones la solución del problema. Para esta constante positiva, se dice que existe un decrecimiento o desintegración de la sustancia, y el caso que sea negativa, hay un crecimiento o incremento.

Muy bien, ya que hemos dado una pequeña introducción de algunos usos de las ecuaciones diferenciales ordinarias, pasemos a ver como podemos aplicarlas para resolver algunos problemas aplicados a distintas áreas.

---

---

Aplicaciones a la Economía

Mostremos una aplicación de las ecuaciones diferenciales para calcular interés compuesto, el cual podemos aplicar bien sea cuando hacemos depósitos a plazos fijos, o incluso para calcular créditos a bancos, entre otras aplicaciones.

Supongamos que un usuario de una banca bien sea pública o privada realiza un deposito de una cierta cantidad de dinero, digamos C₀ en una entidad bancaria que paga a sus ahorristas, intereses a una tasa del 6%. Este usuario quisiera tener una proyección del valor de su inversión al cabo de t años.

Para poder determinar esa cantidad, depende de la frecuencia con la cual se compone el interés. Es por ellos que mostraremos el efecto que tiene la frecuencia con la que se compone el interés.

Ahora bien, si el interés se compone una sola vez al año, entonces se sabe de la teoría que la ecuación es:

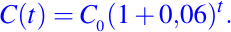
Si ahora, el interés se compone 2 veces al año, entonces su ecuación es:

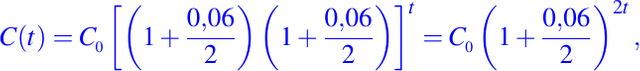
y en general, cuando el interés se compone k veces al año, la ecuación que modela este interés es:

Haciendo una aproximación del ejemplo de manera real, a través de un modelo matemático, donde vamos a suponer que el interés se compone de forma continua. Entonces, podemos escribir la ley de crecimiento de la inversión en la forma de una ecuación diferencial, de la forma siguiente:

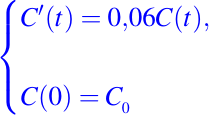
donde para calcular su solución podemos aplicar el método visto en la Lección #1, de esta manera tenemos:

---

Observación: Notemos lo siguiente, si en el segundo miembro de la igualdad dada en (6) obtenemos el segundo miembro de la igual en (7), esto debido al siguiente hecho:

---

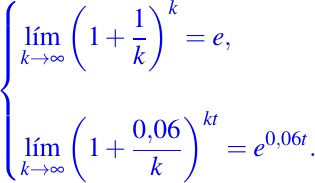
La anterior observación lo que nos hace ver es como el modelo discreto y el modelo continuo son equivalentes. Mostremos una tabla de datos, para analizar de mejor manera el modelo descrito ya. Para ellos supongamos que la inversión inicial es de 1.000 Bs. S. En la misma mostraremos las comparaciones de tres modelos, calculando el rendimiento. En estas comparaciones primero mostraremos el modelo continuo dado en (7), luego usaremos el modelo discreto dado en (6) donde el interés compuesto es cuatro veces al año, es decir, un interés compuesto trimestralmente, y en la tercera columna el mismo modelo continua de (6) donde el interés se compone diariamente, es decir, k=365.

Años	C(t)/C0 en (7)	C(t)/C0 en (6) con k=4	C(t)/C0 en (6) con k=365
1	1,0618	1,0614	1,0618
2	1,1275	1,1265	1,1275
5	1,3499	1,3369	1,3498
10	1,8221	1,8140	1,8220
20	3,3201	3,2907	3,3198

Como podemos apreciar, en la mayoría de los casos la frecuencia con la que se compone el interés no es de suma importancia. Se podría tener una importancia significativa si la inversión es muy grande y con tasas de interés más altas. Pero incluso si la inversión es alta, y la tasa de interés es pequeña, el interés generado podría ser significativo.

---

---

Aplicaciones en Química

Una reacción química de segundo orden implica la interacción (colisión) de una molécula de una sustancia P con una molécula de una sustancia Q, para producir una molécula de una nueva sustancia X;

la cuál es la notación usual. Suponga que p y q son las concentraciones iniciales de las sustancias P y Q respectivamente, y sea x(t) la concentración de X en el instante t. Entonces,

son las concentraciones de P y Q en el instante t y la rapidez a la que ocurre la reacción la describe la ecuación diferencial siguiente:

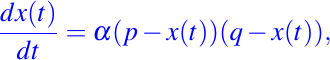
donde alpha es una constante positiva.

1. Si x(0)=0, encuentre la solución del problema.x(t).
2. Si las sustancias P y Q son las mismas, entonces la ecuación se transforma en:
   
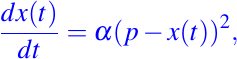
   si x(0)=0, encuentre x(t).

---

1. Para resolver este problema es necesario identificar el método que podemos usar para resolverlo. Como podemos observar, la ecuación, del lado derecho de la igualdad solo depende de x(t), ya que tanto p como q son cantidades constantes, por lo tanto el método que usaremos para resolverla, es el método de separación de variables. El cual pueden consultar en la Lección #2 de esta serie. Por lo tanto la solución general del problema viene dada por la ecuación siguiente:
   
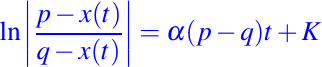
   usando la condición inicial, obtenemos la constantes K, y sustituyendo en la ecuación anterior tenemos:
   
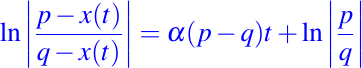
   Así, para despejar x(t) debemos realizar operaciones algebraicas, teniendo en cuenta propiedades de la función exponencial y la función logarítmica, y obtenemos nuestra expresión de la solución particular del problema, la cual queda expresada de la forma siguiente:
   
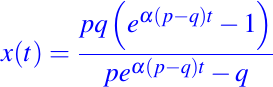
2. Ahora cuando las sustancias son las mismas, entonces la ecuación diferencial que se obtiene es:
   
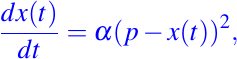
   Similarmente al caso anterior, el método que usaremos será el método de variables separables, por lo tanto la solución general es de la forma:
   
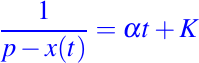
   usando la condición inicial obtenemos:
   
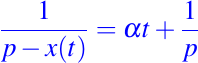
   así despejando x(t) de la ecuación anterior, tenemos:
   

---

---

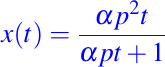
Queridos amigos y lectores, espero hayan disfrutado de esta 8va entrega de la serie de Introducción a las Ecuaciones Diferenciales, de igual manera los invito para la próxima entrega de esta serie, donde continuaremos tratando este tema tan interesante e importante y de mucha aplicación en la ciencia e ingeniería. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y sus aplicaciones. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias.

• Beléndez, Augusto. Ecuaciones diferenciales ordinarias. Métodos Matemáticos de la Física. 1987.
• Hartman, Philip. Ordinary differential equations. (2002).
• Coddington, Earl A., and Norman Levinson. Theory of ordinary differential equations. McGraw-Hill Education, 1955.
• Boyce, William E., Richard C. DiPrima, and Charles W. Haines. Elementary differential equations and boundary value problems. Vol. 9. New York: Wiley, 1969.

---

También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales, que estoy seguro serán de su interés:

Lección #1	Lección #2	Lección #3
Lección #4	Lección #5	Lección #6
Lección #7

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath con
, y GIMP.

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}