Angulo sólido subtendido por una de las caras de un cubo con respecto a un punto situado en el centro del mismo
Reciban mis cordiales saludos toda la comunidad de Steemit, especialmente la comunidad relacionada con el proyecto @steemstem y @stem-espanol, con sus etiquetas #steemstem y #stem-espanol. Saludos mis muy queridos y atentos Steemians-Lectores. Después de ausentado por un tiempo debido a quebrantos de salud, aquí estoy nuevamente compartiendo con todos ustedes interesantes temas de ciencia. En esta oportunidad decidí mostrarles, mediante una presentación bien detallada y didáctica, la forma de calcular el ángulo sólido subtendido por una de las caras de un cubo con respecto a un punto situado en el centro del mismo. Todo esto lo hago con la finalidad de hacer más fácil de entender todos los procedimientos involucrados.
Mis estimados Steemians-Lectores, en posts anteriores les presenté la teoría que considero necesaria para entender bien lo que es el Angulo Sólido. Estos posts son los siguientes:
- EL ANGULO SOLIDO - PARTE 1 - CONOCIMIENTOS BASICOS.
- EL ANGULO SOLIDO - PARTE 2 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 3 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 4 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 5 - DEFINICION DE ANGULO SOLIDO.
- EL ANGULO SOLIDO - PARTE 6 - EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO.
- EL ANGULO SOLIDO - PARTE 7 - PROPIEDADES DEL ANGULO SOLIDO.
Todos los anteriores posts los elaboré con la finalidad de tener un buen y abundante apoyo teórico sobre el Angulo Sólido, el cual suele ser muy escaso en los textos que podemos encontrar donde esta definición está involucrada.
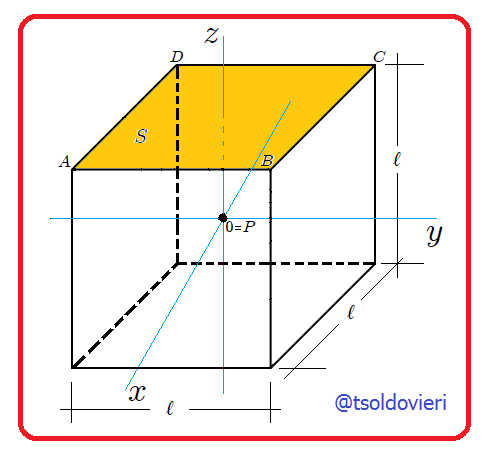
en cuyo centro se ha colocado el origen 
de un sistema de coordenadas Cartesianas y con respecto al cual se desea calcular el ángulo sólido 
subtendido por la cara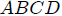 
.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
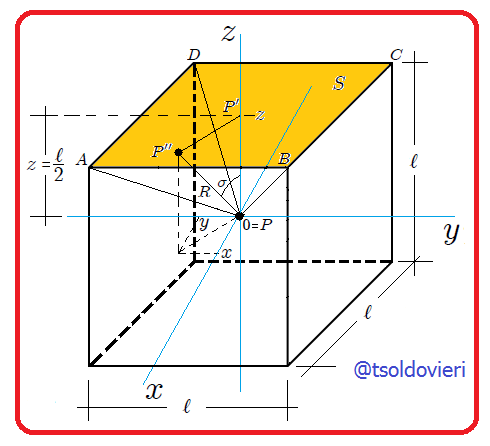
Mis amigos Steemians, en la figura 1 les muestro un cubo de lado 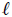en cuyo centro he colocado el origen 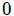de un sistema de coordenadas Cartesianas. Deseamos calcular el ángulo sólido 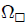subtendido por una de sus caras, en este caso la cara 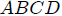, con respecto a un punto 
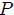situado en su centro. El cálculo lo haré usando coordenadas Cartesianas y coordenadas cilíndricas.
En coordenadas Cartesianas:
Mis Steemians-Lectores, el ángulo sólido 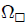viene dado a partir de la definición 6 en el post EL ANGULO SOLIDO - PARTE 6 - EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO. mediante,
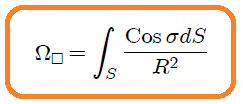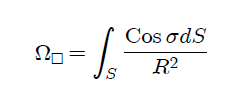
Si usamos coordenadas Cartesianas, como les muestro en la figura 2, es fácil encontrar al observar el triángulo 
que se cumplen las expresiones,
, en coordenadas Cartesianas, subtendido por la cara con respecto al punto ubicado en el centro del cubo.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
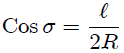
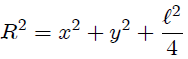
Si sustituimos primero (2) y después (3) en (1) obtenemos,
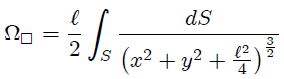
pero en coordenadas Cartesianas sabemos que,
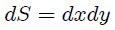
por lo que podemos escribir (4) como,
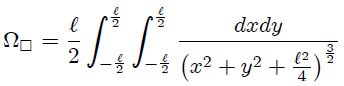
donde he tenido presentes los límites de integración para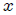 
y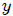 
en concordancia con lo mostrado en la figura 2.
Mis Steemians-Lectores, resolvamos primero la integración con respecto a 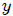. Utilizando 1.2.43.-17 (página 92) de la referencia 3 escrita para ,
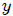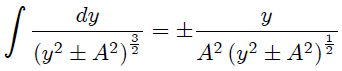
con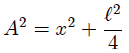 
nos resulta,
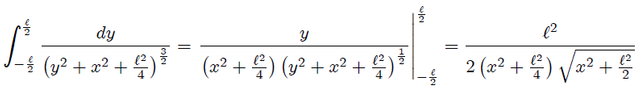
por lo cual (6) nos queda ahora como,
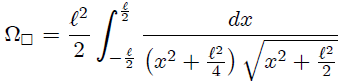
Si ahora, mis amigos Steemians-Lectores, utilizamos 1.2.45-10 (página 94) de la referencia 3,
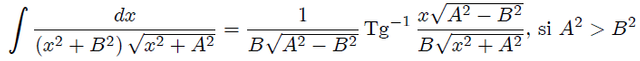
con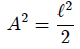 
y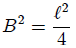 
nos resulta,
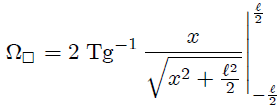
de donde finalmente,
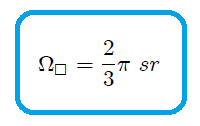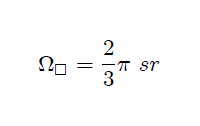
Este resultado era de esperarse, mis estimados y atentos Steemians-Lectores. En efecto, el ángulo sólido subtedido por las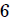 
caras del cubo con respecto al punto 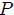es de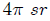 
por cubrir todo el espacio (como ocurre para una esfera), entonces el subtendido por una de sus caras es 
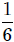de este valor, es decir,
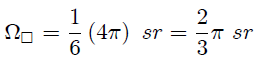
En coordenadas cilíndricas:
Para facilitar los cálculos mis Steemians-Lectores, encontraremos primero el ángulo sólido subtendido por la octava parte de la cara del cubo que es el triángulo rectángulo 
de la figura 3, donde les muestro también las coordenadas cilíndricas de que son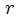 
, 
, 
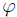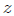. De esta figura y a partir del triángulo 
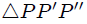es fácil que encontremos,
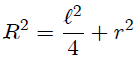
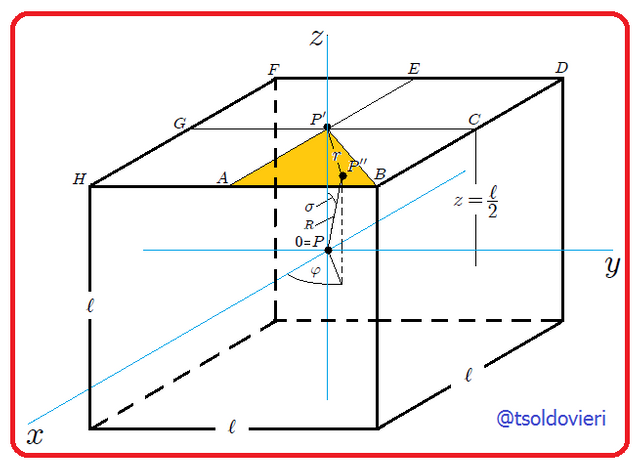
subtendido por la porción 
de la cara 
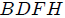del cubo con respecto al punto 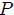.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
manteniéndose la expresión (2). Entonces, al sustituir primero (2) y luego (9) en (1) nos resulta,
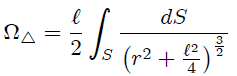
pero, mis atentos Steemians-Lectores, sabemos que en coordenadas cilíndricas,
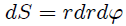
por lo cual (10) se puede escribir ahora como,
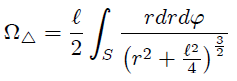
El problema ahora aquí, mis atentos Steemians-Lectores, es establecer los límites de integración. Las variables 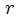y 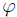están relacionadas por la ecuación de la recta que contiene al segmento 
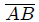que condiciona el límite superior para 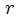como se puede observar en la figura 4 (el inferior es 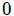como fácilmente se puede observar). En efecto, a partir del triángulo 
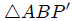podemos escribir,
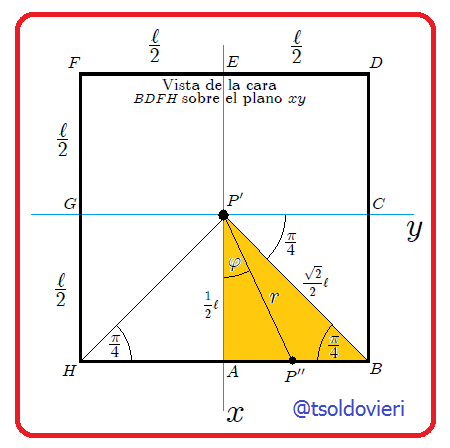
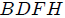sobre el plano 
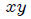con la finalidad de obtener el límite superior para 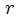en la integral (12).(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
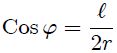
de donde,
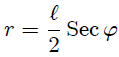
que es la ecuación de la recta que contiene al segmento 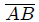, proporcionando el límite superior de la variable 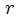. Ahora bien, en vista del anterior resultado (12) la podemos escribir ahora como,
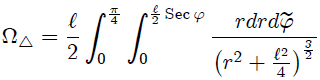
donde he usado la tilde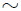 
para distinguir entre variables y límites de integración. Los límites para 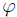los podemos determinar fácilmente a partir de la figura 4. Ahora, si integramos (15) obtenemos,
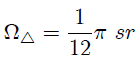
Finalmente, el ángulo sólido 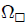subtendido por la cara 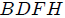es,
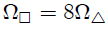
de donde,
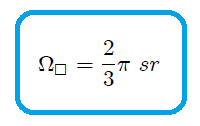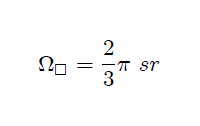
como habíamos obtenido a partir de coordenadas Cartesianas.
BIBLIOGRAFIA CONSULTADA Y RECOMENDADA
Mis estimados Steemians-Lectores, les presento 7 textos y un sitio web. El primero es un texto dedicado completamente al Angulo Sólido, siendo un texto único en su estilo pues no he sabido de otros textos dedicados únicamente a este tema. Los textos del 2 al 3 y del 5 al 7 sólo le dedican una pequeña sección al Angulo Sólido, lo cual es común en los textos encontrados en la literatura relacionada. En el texto 5 podemos encontrar una reseña un poco más completa ya que se le dedica un capítulo (poco extenso). La web 8 muestra el problema abordado en este post pero de una forma simplificada (en extremo), lo cual la hace difícil de asimilar. Se indican en cada caso las páginas correspondientes.
Soldovieri C., T. & Viloria A., T. EL ANGULO SOLIDO Y ALGUNAS DE SUS APLICACIONES. Preprint, 2018. El preprint puede ser descargado de la página http://www.cmc.org.ve/tsweb. Página 63.
Tipler, P. A. & Mosca, G. PHYSICS FOR SCIENTISTS AND ENGINEERS. W. H. Freeman and Company, 6th edition, 2008. Página 753.
Prudnikov, A. P.; Brychkov, Y. A. & Marichev, O. I. INTEGRALS AND SERIES: ELEMENTARY FUNCTIONS, volume 1. Taylor & Francis, 1998. Páginas 92 y 94.
Faget, J. & Mazzaschi, J. TEMAS PROGRAMADOS DE FISICA - GENERALIDADES, volume 1. Editorial Reverté, S.A., 1976. pp. 121 - 135. Página 123.
Kaufman, A. A. GEOPHYSICAL FIELD THEORY AND METHOD - GRAVITATIONAL, ELECTRIC AND MAGNETIC FIELDS, volume A. Academic Press, INC., 1992. Páginas 12 - 22.
Eyges, L. THE CLASSICAL ELECTROMAGNETIC FIELDS. Dover Publications, 1972. Páginas 12 - 22.
Alonso, M. & Finn, E. J. FISICA - MECANICA, volume 1. Fondo Educativo Interamericano, S.A., 1970. Páginas 22.
Weisstein, E. W. SOLID ANGLE. MathWorldA Wolfram Web Resource. http://mathworld.wolfram.com/SolidAngle.html.
Estimados amigos Steemians-Lectores. Espero que la anterior información les sea de mucha utilidad. Como ya es costumbre, si tienen preguntas no duden en hacérmelas llegar pues, con mucho gusto, les atenderé. Igualmente, si tienen detalles que puedan nutrir o mejorar la anterior información, por favor, háganmelas saber. Hasta mi próximo post ¡Saludos a todos! 😁.
Si deseas leer más artículos científicos de buena calidad, no pierda el tiempo, visite las etiquetas #steemstem y #stem-espanol. Es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Unete al canal de @steemstem. También puedes visitar el blog @steemstem y obtener mas información.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Muchas gracias por el constante apoyo @entropia. Gracias también por la participación en la mención especial. Saludos.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for the support @steemstem. Regards.
Un post de buena calidad, profesor @tsoldovieri. Saludos.
Te invito a unirte al servidor en Discord de #STEM-Espanol, donde puedes participar y recibir más feedback.
Muchas gracias @eniolw. Gracias por la invitación, trataré de hacerlo pues mi internet es muy inestable y limitada. Mis cordiales saludos.
Saludos, hermano. Tenia tiempo que no lei algo suyo. De verdad muy interesante. Tuve que leerme todos tus post para poder entender este. Asi que aprendi algo nuevo para mi.
Lo que no consegui en ninguno de tus escrito es una aplicación práctica etc. Viendo lo del angulo solido en un esfera (en tus post anteriores) me parece que seria interesante su aplicación en los GPS. No recuerdo bien donde lei que lo del GPS su dificultad radicaba en resolver un problema matematico topologico. Quien quita y sea Ud. el responsable de ese acertijo....
SALUTATIONS DU VENEZUELA
Gracias por pasarte por aquí , comentar y apoyarme mi hermano @soy-venezuelien. Gracias por leer mis anteriores posts. Estuve ausente por un tiempo debido a un quebranto de salud que ya superé. Si, aún no he presentado las aplicaciones del concepto de Angulo Sólido, que no son pocas. Esto lo haré en un post más adelante después de mostrar otros dos o tres post donde presente ejemplos del cálculo del mismo, como lo hice en el presente post. Se ve interesante lo del GPS, habría que ver. Saludos.
Saludos amigo @tsoldovieri!. Excelente publicación, como siempre muy didáctica y de sencilla comprensión.
Muchas gracias amiga @ufv por apoyar con frecuencia mis posts. Saludos.
Excelente explicación hermano, muy didáctico. Saludos.
Muchas gracias por tu comentario y apoyo mi amigo y colega @rnunez09. Saludos.
Es grato saludarlo estimado @tsoldovieri, excelente artículo hermano bien detallado, gran esfuerzo, nos seguimos leyendo !
Es grato también para mi verlo por mi blog. Gracias por su motivador comentario.
¡Mis cordiales saludos!
Buen trabajo @tsoldovieri . Tu puedes generalizar estos cálculos en coordenadas curvilíneas?
Gracias por tu comentario y apoyo mi estimado @germanmontero. Claro, se puede hacer. Saludos.
Saludos estimado @tsoldovieri. Como de costumbre un trabajo de calidad con la didáctica que lo caracteriza. gracias por compartir.
Muchas gracias por tu comentario y apoyo mi estimado @lorenzor. Saludos.
Excelente @tsoldovieri, muy buen aporte de saberes matemáticos debidamente detallado e ilustrado para una buena comprensión por parte de la comunidad!! Saludos cordiales!!
Muchísimas gracias por tu motivador comentario y apoyo @reinaseq. Ya te estoy siguiendo, sígueme si es de tu agrado. Saludos cordiales.