EL ANGULO SOLIDO - PARTE 7 - PROPIEDADES DEL ANGULO SOLIDO
Cordiales y muy afectuosos saludos a toda la comunidad de Steemit. Aquí estoy muy contento por la aceptación que han comenzado a tener mis publicaciones relacionadas con la ciencia, lo cual me incentiva a trabajar mucho más fuerte por crear publicaciones de calidad. Gracias a todos por su gran apoyo, muy especialmente @steemstem. Agradezco @steemstem por crear el tag stem-espanol que facilita el trabajo de nosotros los hispanoparlantes. Continuando con mi serie de posts dedicados a la definición de ANGULO SOLIDO, en el presente les muestro LAS PROPIEDADES DEL ANGULO SOLIDO. Todos estos posts los voy presentando de una manera pausada ya que requieren de considerable trabajo de edición de texto y creación de figuras. Es importante destacar que TODAS LAS IMAGENES AQUI PRESENTADAS SON, COMPLETAMENTE, DE MI AUTORIA. Disculpen lo extenso y por el abundante contenido matemático, pero es completamente necesario para lograr un excelente entendimiento de las propiedades del Angulo Sólido.
INDICE DE POSTS ANTERIORES:
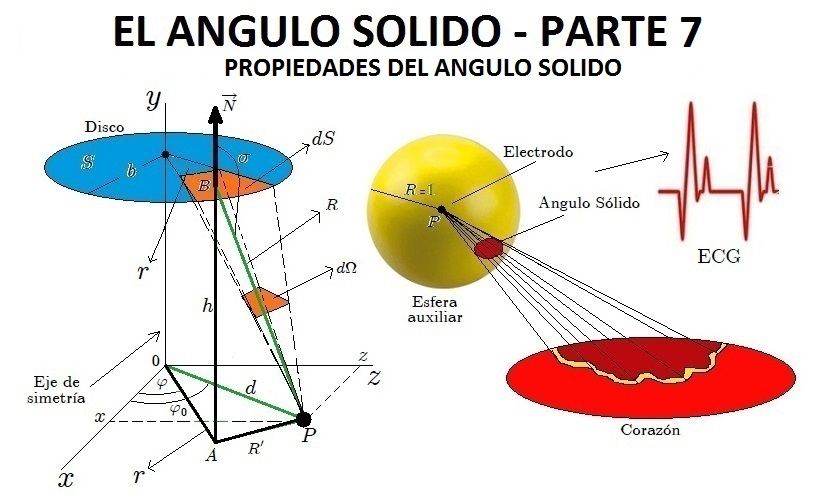
PROPIEDADES DEL ANGULO SOLIDO
El Angulo Sólido posee algunas propiedades interesantes. Estas son las siguientes:
PROPIEDAD 1
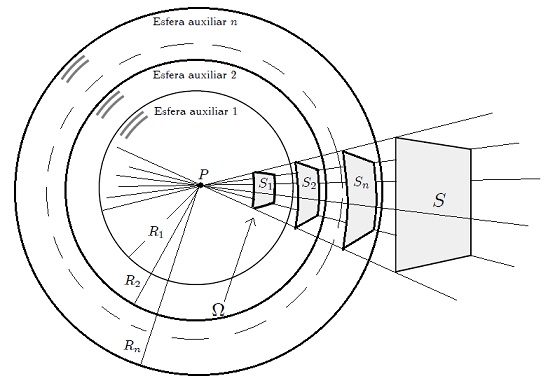
Cualquiera que sea el tamaño de la esfera auxiliar, el ángulo sólido 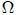 subtendido por una superficie abierta subtendido por una superficie abierta 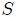 con respecto a un punto con respecto a un punto 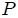 se mantendrá constante, si se mantiene también constante la distancia entre ambos. se mantendrá constante, si se mantiene también constante la distancia entre ambos. |
|---|
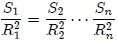 . Por esta razón
. Por esta razón 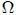 sirve para identificar cada ángulo sólido.
sirve para identificar cada ángulo sólido.Esta propiedad es debida a la homotecia vista en el post EL ANGULO SOLIDO - PARTE 1. Al igual como ocurre con los ángulos planos, si con centro en el punto 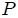 de la figura 1 se traza una esfera auxiliar de radio
de la figura 1 se traza una esfera auxiliar de radio 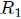 , se obtiene una superficie
, se obtiene una superficie 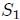 de manera que su cociente da como resultado la medida del ángulo sólido
de manera que su cociente da como resultado la medida del ángulo sólido 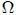 subtendido por el rectángulo con respecto a dicho punto. Si para la misma disposición se traza una nueva esfera auxiliar de radio
subtendido por el rectángulo con respecto a dicho punto. Si para la misma disposición se traza una nueva esfera auxiliar de radio 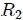 con centro en
con centro en 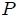 se obtiene una superficie
se obtiene una superficie 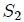 dando su cociente como resultado la misma medida
dando su cociente como resultado la misma medida 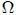 y así sucesivamente, es decir,
y así sucesivamente, es decir,
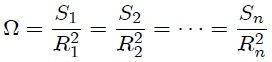
PROPIEDAD 2
El ángulo sólido 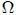 subtendido por una superficie abierta subtendido por una superficie abierta 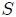 con respecto a un punto con respecto a un punto 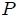 , es igual a la superficie que resulta sobre la superficie de una esfera unitaria centrada en , es igual a la superficie que resulta sobre la superficie de una esfera unitaria centrada en 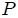 , debido a la intersección de las líneas rectas que van desde , debido a la intersección de las líneas rectas que van desde 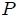 (que en conjunto forman un cono) hasta el perímetro de (que en conjunto forman un cono) hasta el perímetro de 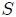 . . |
|---|
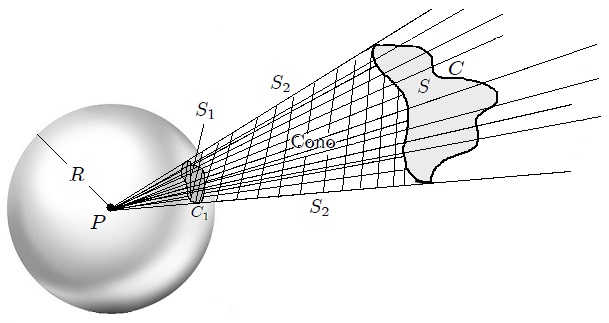
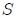 sobre la superficie de la esfera auxiliar de radio
sobre la superficie de la esfera auxiliar de radio 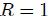 .
.Considérese la figura 2. En esta figura 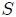 es una superficie abierta cuyo ángulo sólido subtendido con respecto a
es una superficie abierta cuyo ángulo sólido subtendido con respecto a 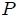 se desea calcular. Para hacer esto, como ya se vio antes, se posiciona una esfera auxiliar de radio
se desea calcular. Para hacer esto, como ya se vio antes, se posiciona una esfera auxiliar de radio 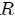 de tal manera que su centro coincida con
de tal manera que su centro coincida con 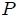 y luego se trazan líneas rectas desde
y luego se trazan líneas rectas desde 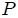 hasta el perímetro
hasta el perímetro 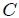 de
de 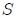 , generándose así un cono con vértice en el mencionado punto. La intersección de las líneas rectas con la superficie de la esfera origina el perímetro
, generándose así un cono con vértice en el mencionado punto. La intersección de las líneas rectas con la superficie de la esfera origina el perímetro 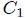 que da forma a la superficie
que da forma a la superficie 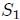 sobre la superficie de la misma. La superficie
sobre la superficie de la misma. La superficie 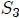 (representada por la zona con entramado) es la formada por la superficie
(representada por la zona con entramado) es la formada por la superficie 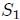 más la superficie
más la superficie 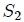 de la pared del cono que se encuentra entre el perímetro
de la pared del cono que se encuentra entre el perímetro 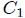 de
de 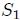 y el perímetro
y el perímetro 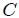 de
de 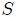 , es decir,
, es decir,
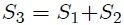
Las superficies 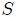 y
y 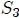 poseen el mismo perímetro
poseen el mismo perímetro 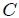 con respecto a
con respecto a 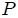 , así mediante la propiedad anterior es posible escribir que,
, así mediante la propiedad anterior es posible escribir que,
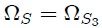
y además, las superficies 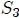 y
y 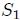 poseen el mismo perímetro
poseen el mismo perímetro 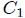 con respecto a
con respecto a 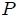 pudiéndose escribir,
pudiéndose escribir,
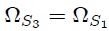
entonces de este resultado y de la ecuación 4 se puede concluir que,
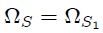
El ángulo sólido 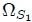 se obtiene como,
se obtiene como,
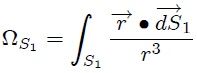
a partir de la definición de ángulo sólido vista en el post EL ANGULO SOLIDO - PARTE 6. Pero aquí 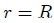 por estar
por estar 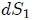 sobre la esfera auxiliar. Supóngase ahora que la esfera es unitaria, es decir,
sobre la esfera auxiliar. Supóngase ahora que la esfera es unitaria, es decir, 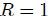 . Entonces,
. Entonces, 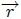 es un vector unitario para
es un vector unitario para 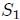 perpendicular a
perpendicular a 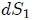 y, por ende, paralelo a
y, por ende, paralelo a 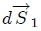 . Por lo tanto,
. Por lo tanto,
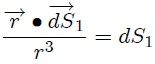
resultando a partir de la ecuación 6 que,
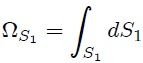
de donde,
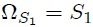
Finalmente, al sustituir el resultado dado por la ecuación 9 en la ecuación 5 se obtiene,
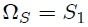
como se quería mostrar.
Por el anterior resultado se puede decir que,
Se define el Angulo Sólido bajo el cual se ve una superficie desde el punto 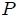 como el área de la proyección cónica de dicha superficie sobre una esfera de radio unidad centrada en como el área de la proyección cónica de dicha superficie sobre una esfera de radio unidad centrada en 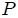 . . |
|---|
PROPIEDAD 3
Dado un cono correspondiente a un ángulo sólido 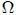 subtendido con respecto a un punto dado subtendido con respecto a un punto dado 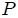 , todas las superficies abiertas que estén inscritas en él subtenderán el mismo ángulo sólido , todas las superficies abiertas que estén inscritas en él subtenderán el mismo ángulo sólido 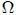 con respecto a dicho punto. con respecto a dicho punto. |
|---|
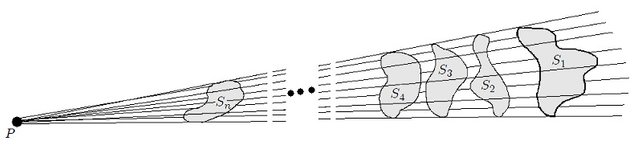
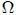 con respecto a un punto de referencia
con respecto a un punto de referencia 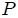 .
.En la figura 3, las superficies abiertas 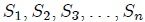 tienen todas curvas perimetrales inscritas en un cono común que tiene vértice en
tienen todas curvas perimetrales inscritas en un cono común que tiene vértice en 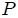 , por lo que todas subtenderán un mismo ángulo sólido
, por lo que todas subtenderán un mismo ángulo sólido 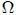 con respecto a dicho punto. Es decir,
con respecto a dicho punto. Es decir,
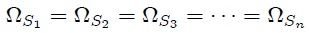
PROPIEDAD 4
Si se tiene una superficie abierta 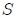 que genera un cono con vértice en que genera un cono con vértice en 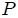 , subtendiendo así un ángulo sólido , subtendiendo así un ángulo sólido 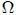 respecto al mismo, entonces toda superficie abierta respecto al mismo, entonces toda superficie abierta 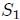 que resulte de la intersección de una superficie abierta que resulte de la intersección de una superficie abierta 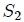 con dicho cono y de tal manera que quede inscrita éste, subtenderá el mismo ángulo sólido que con dicho cono y de tal manera que quede inscrita éste, subtenderá el mismo ángulo sólido que 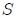 con respecto al mismo punto. con respecto al mismo punto. |
|---|
Lo anterior se representa gráficamente en la figura 4(a), para el caso en que la intersección se dé entre 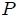 y la superficie
y la superficie 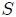 y en la figura 4(b), para el caso en que la intersección se dé más allá de
y en la figura 4(b), para el caso en que la intersección se dé más allá de 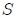 .
.
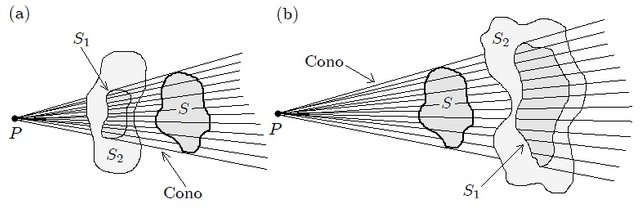
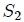 con el cono generado por una superficie abierta
con el cono generado por una superficie abierta 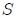 con respecto a un punto
con respecto a un punto 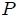 , en la que se obtiene una superficie
, en la que se obtiene una superficie 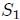 : (a) intersección entre
: (a) intersección entre 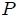 y
y 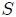 , (b) intersección más allá de
, (b) intersección más allá de 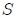 .
.Como la superficie 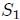 resultante de la intersección está inscrita en el cono generado por
resultante de la intersección está inscrita en el cono generado por 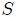 con respecto a
con respecto a 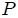 , entonces por la propiedad 3 resulta que,
, entonces por la propiedad 3 resulta que,
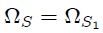
PROPIEDAD 5
Los ángulos sólidos subtendidos por dos superficies 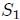 y y 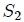 , que comparten el mismo perímetro , que comparten el mismo perímetro 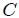 con respecto a un punto con respecto a un punto 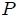 externo a ambas, subtienden ángulos sólidos iguales y opuestos en signo respecto a dicho punto. externo a ambas, subtienden ángulos sólidos iguales y opuestos en signo respecto a dicho punto. |
|---|
Considérese la figura 5. En dicha figura se muestran dos superficies 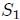 y
y 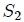 que poseen el mismo perímetro
que poseen el mismo perímetro 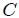 con respecto al punto
con respecto al punto 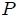 y que juntas forman la superficie cerrada
y que juntas forman la superficie cerrada 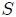 . El perímetro
. El perímetro 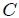 está determinado por todos los puntos de tangencia de la superficie cónica sobre la superficie cerrada
está determinado por todos los puntos de tangencia de la superficie cónica sobre la superficie cerrada 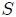 .
.
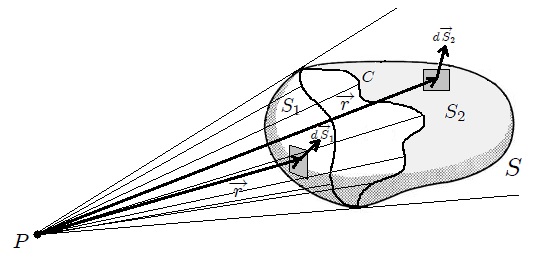
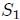 y
y 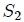 que poseen el mismo perímetro
que poseen el mismo perímetro 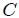 con respecto al punto
con respecto al punto 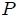 y que juntas forman la superficie cerrada
y que juntas forman la superficie cerrada 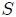 .
.En el caso de la superficie 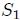 , su diferencial de superficie
, su diferencial de superficie 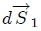 apunta hacia adentro de
apunta hacia adentro de 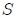 y en el caso de
y en el caso de 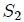 , su diferencial de superficie
, su diferencial de superficie 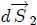 apunta hacia afuera de la misma. Si el diferencial de superficie
apunta hacia afuera de la misma. Si el diferencial de superficie 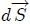 de
de 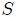 es definido de tal manera que apunte siempre hacia afuera de la misma, entonces el ángulo sólido total
es definido de tal manera que apunte siempre hacia afuera de la misma, entonces el ángulo sólido total 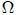 vendrá dado por,
vendrá dado por,
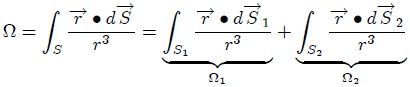
donde se ha usado la definición de ángulo sólido vista en el post EL ANGULO SOLIDO - PARTE 6. Pero a partir de Teorema de Divergencia Gauss (ver referencia 5),
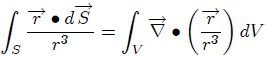
donde 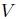 es el volumen encerrado por
es el volumen encerrado por 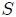 con
con 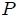 fuera del mismo. Para resolver la integral de la derecha, se desarrollará primero su integrando. En efecto,
fuera del mismo. Para resolver la integral de la derecha, se desarrollará primero su integrando. En efecto,
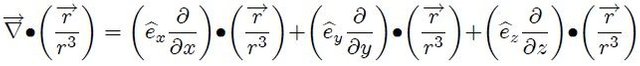
puesto que 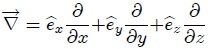 . Pero,
. Pero,
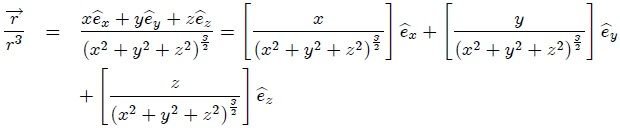
ya que 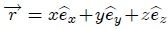 y
y 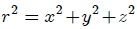 . Entonces, al sustituir la ecuación 16 en la ecuación 15 resulta,
. Entonces, al sustituir la ecuación 16 en la ecuación 15 resulta,
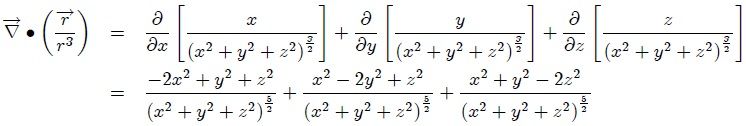
de donde,
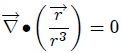
Ahora, si se sustituye este resultado en la ecuación 14 se obtiene,
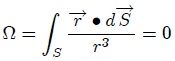
que al ser sustituida en la ecuación 13 da como resultado final que,
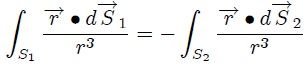
de donde,
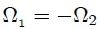
PROPIEDAD 6
El ángulo sólido 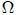 subtendido por una superficie cerrada subtendido por una superficie cerrada 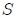 con respecto a un punto con respecto a un punto 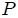 externo a la misma, es nulo. externo a la misma, es nulo. |
|---|
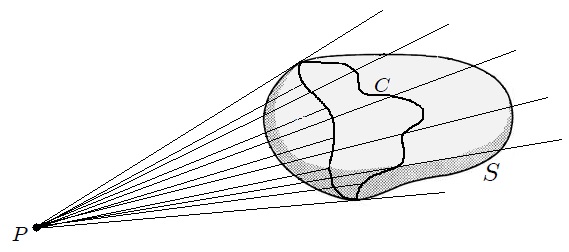
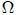 subtendido por una superficie cerrada
subtendido por una superficie cerrada 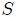 con respecto a un punto
con respecto a un punto 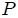 externo a la misma.
externo a la misma.Esta propiedad es consecuencia de la propiedad 5 y está demostrada por la ecuación 19. La situación descrita se muestra en la figura 6, donde la curva perimetral 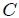 está formada por todos los puntos tangentes sobre
está formada por todos los puntos tangentes sobre 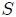 de las semirrectas que parten de
de las semirrectas que parten de 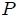 y pasan por los bordes de la misma. Nótese que, nuevamente, se tiene la situación representada en la figura 4 por lo que,
y pasan por los bordes de la misma. Nótese que, nuevamente, se tiene la situación representada en la figura 4 por lo que,
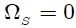
PROPIEDAD 7
El ángulo sólido 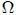 subtendido por una superficie cerrada subtendido por una superficie cerrada 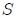 con respecto a un punto con respecto a un punto 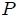 interno a la misma es interno a la misma es 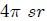 . . |
|---|
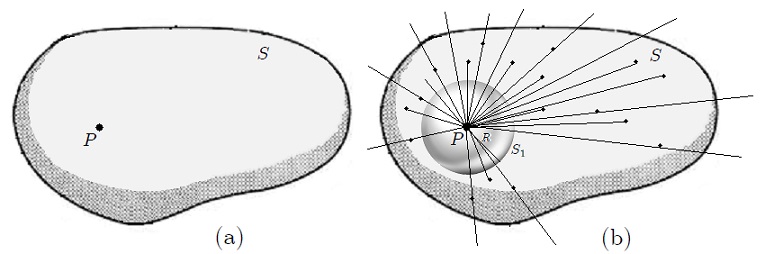
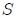 con un punto
con un punto 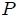 en su interior, respecto del cual se desea calcular el ángulo sólido
en su interior, respecto del cual se desea calcular el ángulo sólido 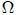 subtendido por la misma. (b) La superficie de la esfera auxiliar quedará completamente cubierta al proyectar
subtendido por la misma. (b) La superficie de la esfera auxiliar quedará completamente cubierta al proyectar 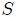 sobre la misma.
sobre la misma.Se tiene una superficie cerrada 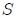 como la mostrada en la figura 7(a) y se desea calcular el ángulo sólido
como la mostrada en la figura 7(a) y se desea calcular el ángulo sólido 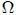 por ella subtendido con respecto al punto
por ella subtendido con respecto al punto 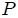 que se encuentra en su interior.
que se encuentra en su interior.
Procediendo de la forma ya descrita, se dibuja una esfera auxiliar unitaria (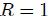 ) en su interior con centro en
) en su interior con centro en 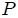 y se procede a proyectar
y se procede a proyectar 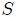 sobre la superficie de la misma, como se muestra en la figura 7(b). Obviamente esta proyección da como resultado toda la superficie
sobre la superficie de la misma, como se muestra en la figura 7(b). Obviamente esta proyección da como resultado toda la superficie 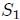 de la esfera auxiliar. Entonces por la propiedad 5 se tiene que,
de la esfera auxiliar. Entonces por la propiedad 5 se tiene que,
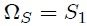
pero,
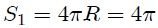
por ser unitaria. Entonces, al sustituir este resultado en la ecuación 23 se obtiene finalmente,
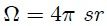
PROPIEDAD 8
Si se tienen dos conos opuestos por su vértice 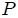 , los ángulos sólidos , los ángulos sólidos 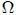 a los que corresponden ambos son iguales. a los que corresponden ambos son iguales. |
|---|
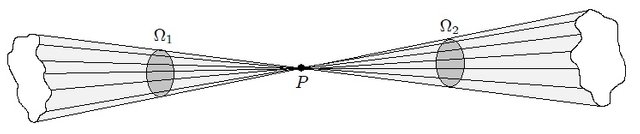
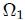 y
y 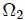 opuestos por el vértice.
opuestos por el vértice.A partir de la figura 8 es realmente obvio llegar a la conclusión de que,
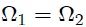
REFERENCIAS
- Soldovieri, Terenzio y Viloria, Tony. EL ANGULO SOLIDO Y ALGUNA DE SUS APLICACIONES. 1era edición (borrador). Puede descargarse en mi web http://www.cmc.org.ve/tsweb/
- Todas las imágenes aquí presentadas fueron elaboradas por mi. La imagen a color constituye una modificación de la imagen de portada del texto indicado antes, del cual soy autor.
- Alonso, M. & Finn, E. J. FISICA - MECANICA, volumen 1. Fondo Educativo Interamericano,
S.A., 1970. pp. 21 - 23 51 - 53. - Faget, J. & Mazzaschi, J. TEMAS PROGRAMADOS DE FISICA - GENERALIDADES, volumen 1. Editorial Reverté, S.A., 1976. pp. 121 - 135.
- Marder, L. CAMPOS VECTORIALES - SELECCION DE PROBLEMAS RESUELTOS, volumen 7. Editorial LIMUSA, 1974. pp. 38-39 63-65.

Como lo he dicho en los posts anteriores, es mi muy sincero deseo que la anterior información les sea muy útil. Sé que dentro de la comunidad de Steemit existe una enorme cantidad de estudiantes de carreras afines a la ciencia, a los cuales esta información puede ser de gran utilidad. El próximo de esta serie se referirá a las Diferenciales notables de ángulo sólido.
Hasta mi próximo post. ¡Saludos a todos! 😁.
Si desea leer más artículos científicos de buena calidad, no pierda el tiempo, y visite la etiqueta #steemstem, es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Unete al canal de @steemstem. También puedes visitar el blog @steemstem y obtener mas información.


Es muy interesante el aporte que haces a la comunidad científica de #stem-espanol con el dasarrollo matemático que expones aquí. Esperamos seguir contando con tus publicaciones
Gracias por tu comentario y apoyo @iamphysical. Claro que seguirán contando conmigo toda la comunidad científica de #stem-espanol y todo el resto de la comunidad de Steemit. Saludos!.
que buen trabajo y con tanta consistencia. Deberias escribir un manual para elaborar figuras y ecuaciones tan bellamente presentadas. Saludos
Es que soy un genio mi muy hermosa colega @emily61 😜. Cuando guste le muestro cómo lo hago. Saludos!.
Te tomaré la palabra. Un abrazo