Aplicaciones de las Ecuaciones Diferenciales Ordinarias | Lección #9

Saludos queridos lectores, bienvenidos nuevamente. Este post es la 9na entrega de la serie Introducción a las Ecuaciones Diferenciales, donde abordaremos el estudio de algunas aplicaciones de las ecuaciones diferenciales ordinarias, en esta publicación trataremos aplicaciones en diversas áreas, como química, economía, física, entre otras. Se tratará de hacerlo de una forma didáctica sin perder de vista el formalismo matemático. La misma está dirigida al público en general, pero con atención especial a estudiantes universitarios de ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Aplicaciones a la Mecánica Elemental

Algunas de las aplicaciones de las ecuaciones diferenciales de 1er orden, las cuales son muy importantes, están dadas en el campo de la mecánica elemental. Es por ellos que dedicaremos esta publicación a hablar sobre ellas, tratando de describirlas ampliamente, y mostrar algunos ejemplos.

Los movimientos de un cuerpo rígido de forma horizontal, o a lo largo de una recta, son de las aplicaciones más usadas en la mecánica elemental. Como sabemos los cuerpos rígidos obedecen las leyes del movimiento o inercia descritas por Newton. La 2da Ley de Newton describe "el producto de la masa del cuerpo por la aceleración es igual a la fuerza externa aplicada al cuerpo". Escrito en lenguaje matemático, tenemos:

donde F es la fuerza externa, m la masa del cuerpo y a es su aceleración en la dirección de F. Si la masa del cuerpo es una cantidad constante, que no depende del tiempo, entonces la ecuación dada en (1) la podemos escribir de la siguiente manera:

donde v(t) es la velocidad y P(t)=mv(t) es el momento lineal del cuerpo.

---

Sea ahora un cuerpo que cae libremente en el vacío, tal que la única fuerza de significante que actúa sobre el cuerpo es la gravedad de la Tierra. Entonces la ecuación (1) que ya describimos anteriormente se transforma de la siguiente forma:

donde w es el peso del cuerpo, y g denota la aceleración debido a la gravedad de la Tierra.

Es de hacer notar, que aunque la masa del cuerpo siempre permanece constante, tanto la gravedad como el peso varían dependiendo de la cercanía del cuerpo con respecto al centro de la Tierra. Es por ello que es importante señalar la expresión general para el peso de un cuerpo de masa m, la cual se puede obtener a partir de la Ley de Newton, y que podemos enunciar como sigue:

donde K es una constante. Cuando x=0, es decir, cuando estamos al nivel del mar, la ecuación toma la forma de la ecuación (3), entonces la constante K es:

y la ecuación general del peso del cuerpo queda determinada por:

---

---

Ejemplo 01:

Supongamos que se dejar caer un objeto desde el reposo, donde el objeto tiene masa m, donde el medio donde se desplaza el objeto ofrece una resistencia proporcional a su rapidez, es decir, es proporcional al modulo de su velocidad instantánea. Si, además tomamos como la fuerza gravitacional constante, entonces encuentre la posición y velocidad del objeto en cualquier instante de tiempo t.

---

Para iniciar a resolver y entender el problema es conveniente, hacer un gráfico del fenómeno físico que se describe.

_{Imagen elaborada por @abdulmath.
En Manjaro Linux, con Karbon. Software Libre.}

Como podemos observar, el peso del objeto que se deja caer, actúa hacia abajo de forma positiva, pero la resistencia, que en general es proporcional al modulo de la velocidad, actúa para impedir el movimiento. Cuando la velocidad es positiva o negativa, en ambos casos, la dirección de la resistencia es hacia arriba. De esta manera, en cualquier caso, por la Ley de Newton se puede escribir entonces como sigue:

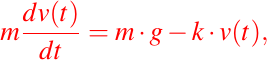
ó

Como podemos observar esta ecuación (5) es una ecuación diferencial lineal de 1er orden. Para resolver esta ecuación, podemos seguir el procedimiento descrito en la Lección #1, así podemos identificar en está ecuación lo siguiente:

entonces la solución de la ecuación diferencial viene dada por la ecuación:

Como el objeto que se deja caer parte del reposo, entonces tiene velocidad inicial cero, es decir, v(0)=0, la que usaremos como nuestra condición inicial para determinar la constante de la solución general, y obtenemos:

y por lo tanto la ecuación de la velocidad y además la solución única del problema de caída libre planteado es:

Ahora, como debemos también determinar la posición del objeto en cualquier instante de tiempo, usamos que la velocidad es la derivada de la función de desplazamiento o posición, entonces tenemos:

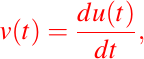
por lo tanto

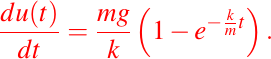
entonces integrando con respecto a t, nos queda

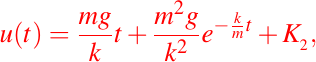
usando la misma condición inicial anterior podemos determinar la constante de integración, y sustituyendo en la solución general, obtenemos la ecuación de desplazamiento o posición, la cuál es:

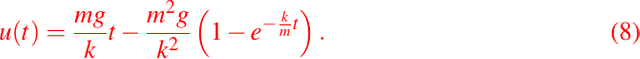
Ahora bien, notemos que si hacemos tender a infinito el tiempo en la ecuación (6) la velocidad tiene a su valor límite, el cuál es:

es decir, que la velocidad límite solo depende de la masa del objeto y del coeficiente de resistencia del medio. Y si tomamos ahora el coeficiente de resistencia tender a cero, la velocidad límite aumenta y se vuelve no acotada.

Otra observación que vale la pena mencionar, es que la resistencia del medio es una función de la rapidez, y cuando suponemos que hay una relación lineal, es solamente razonable para magnitudes de la velocidad bajas, ya que cuando la rapidez es una cantidad muy grande en magnitud, es necesario pensar y suponer que la resistencia del medio es proporcional a alguna potencia de la velocidad, y en algunos casos podría estar dada por una función polinomial de la velocidad.

---

---

Ejemplo 02:

Si lanzamos un cuerpo de masa constante hacia arriba, desde la superficie de la Tierra, con una velocidad v₀, suponemos que no hay resistencia del aire, y tenemos que tener en cuenta que el campo gravitacional varía respecto a la altura con respecto al centro de la Tierra, planteamos encontrar la velocidad inicial mínima que se necesita que el cuerpo tenga para que no regrese a la Tierra, esta velocidad es la que se conoce como "velocidad de escape".

---

Para iniciar a resolver y entender el problema es conveniente, hacer un gráfico del fenómeno físico que se describe.

_{Imagen elaborada por @abdulmath.
En Manjaro Linux, con Karbon. Software Libre.}

Como podemos apreciar en la figura, la única fuerza que actúa sobre el cuerpo es el peso, la misma ejerce su fuerza hacia abajo, por lo tanto la ecuación de desplazamiento o movimiento y la condición inicial, forman un Problema de Valor Inicial (PVI) planteado como sigue:

observemos que la parte derecha de la ecuación anterior solo depende de la variables x, en vez de la variable , entonces es necesario realizar un cambio de variable, y aplicar la regla de la cadena de la siguiente manera:

luego el PVI mostrado en (10) nos queda expresado ahora de la siguiente manera:

para resolver esta ecuación diferencial, debemos usar el método de separación de variables, el cuál vimos en la Lección #2, entonces la solución general esta dada por:

usando la condición inicial obtenemos que la constante viene dada por:

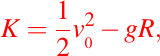
por lo tanto la solución única del problema planteado es:

---

---

Queridos amigos y lectores, espero hayan disfrutado de esta 9na entrega de la serie de Introducción a las Ecuaciones Diferenciales, de igual manera los invito para la próxima entrega de esta serie, donde continuaremos tratando este tema tan interesante e importante y de mucha aplicación en la ciencia e ingeniería. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y sus aplicaciones. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias.

• Beléndez, Augusto. Ecuaciones diferenciales ordinarias. Métodos Matemáticos de la Física. 1987.
• Hartman, Philip. Ordinary differential equations. (2002).
• Coddington, Earl A., and Norman Levinson. Theory of ordinary differential equations. McGraw-Hill Education, 1955.
• Boyce, William E., Richard C. DiPrima, and Charles W. Haines. Elementary differential equations and boundary value problems. Vol. 9. New York: Wiley, 1969.

---

También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales, que estoy seguro serán de su interés:

Lección #1	Lección #2	Lección #3
Lección #4	Lección #5	Lección #6
Lección #7	Lección #8

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath con
, y GIMP.

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}