Geometría analítica y Cinemática (Parte V)


Continuamos con la temática geometría analítica plana, en donde, seguimos fortaleciendo el carácter analítico de las matemáticas, en esta oportunidad nos mantenemos con el análisis entre el maravilloso nexo de la espectacular ciencia física y las imprescindibles matemáticas, esta última representada por la geometría analítica la cual ha servido de base fundamental para la descripción de importantes trayectorias llevadas a cabo por innumerables partículas, cuerpos u objetos presente en nuestro complejo pero maravilloso universo, dichas trayectorias las hemos analizado tanto desde el punto de vista del sistema solar así como desde la visión terrestre, realizando o llevando a cabo de esta manera el maravilloso fenómeno del movimiento.
Cada uno de nosotros somos testigos de los distintos tipos de movimiento que ocurren a nuestro alrededor debido a que el mismos se encuentra inmerso en la naturaleza y desde allí los hemos podido transmitir a las diferentes actividades del ser humano a través de la ciencia física esencialmente por medio de la cinemática y otras áreas complementarias relacionadas con el estudio del movimiento.
Es importante resaltar que de acuerdo a la trayectoria transitada por un cuerpo determinará el tipo de movimiento ejecutado, es decir, está relacionado con el lugar geométrico de la figura recorrida por dichos cuerpos como pudimos comprobar en las pasadas publicaciones, en donde a través de la circunferencia obtuvimos el movimiento circular, la parábola el movimiento parabólico, la elipse el movimiento elíptico y mediante la hipérbola el movimiento hiperbólico cada cual con sus respectivas características y formulaciones matemáticas ideales para su debido entendimiento o comprensión.
La finalidad de este análisis es seguir describiendo algunos de tantos elementos esenciales que unen a estas ramas científicas como ya lo hemos comprobado en las publicaciones antes mencionadas, ahora le corresponde a la esencial línea recta ofrecer sus aportes en el análisis de tan importante fenómeno uniéndola con figuras curvilíneas tales como la circunferencia y parábola para combinar trayectorias rectilíneas con circulares y parabólicas las cuales han sido de gran utilidad en nuestro desarrollo en todos los niveles.
Este análisis lo iniciaremos con la descripción geométrica de la importante línea recta debido a que la misma representa la trayectoria del fenómeno denominado movimiento rectilíneo, de igual forma seguiremos con una breve explicación de la circunferencia y su conocida implementación en el movimiento circular y de igual forma lo haremos con la parábola y su respectivo movimiento, por lo tanto, la intención es mostrar de manera o forma general la importancia de estas tres espectaculares figuras geométricas en el estudio del mencionado fenómeno.

Comprobamos en el análisis de los anteriores movimientos que la física ha podido alimentarse de las extraordinarias figuras geométricas como las cónicas, sin embargo, existe una esencial figura base la cual todos conocemos como línea recta de la cual todos hemos podido aprender y en consecuencia obtener las múltiples formas o cuerpos geométricos en sus distintas dimensiones, esta figura base representa nuestro principio elemental para la comprensión de la ciencia de las formas, figuras o cuerpos geométricos, es decir, la geometría en general.
La firme intención de comprender cada vez más nuestros fenómenos naturales nos ha llevado positivamente a realizar extraordinarios nexos entre nuestras ramas científicas, en donde, las misma adecuadamente se nutren una de la otra para complementarse y lograr su primordial objetivo en pro de la humanidad, lo hemos visto y demostrado con la física a través de la cinemática la cual conjuntamente con las matemáticas por medio de la geometría analítica lograr conformar un lenguaje universal que permite a cualquier persona de nuestra sociedad (si se lo propone) poder interpretar y entender cualquier tipo de fenómeno, en especial, el movimiento.
La línea recta es sin lugar a dudas la figura base para todos aquellos cuerpos geométricos que nos rodean o conforman nuestro medio ambiente, razón por la cual la misma representa la piedra angular para el desarrollo de cualquier área científica, y la cinemática conjuntamente con la geometría analítica han aprovechado tales virtudes para concretar y profundizar el estudio del movimiento, por lo tanto, todo conocimiento complejo siempre estará ligado a sus raíces o bases como lo ha sido la línea recta para la cinemática y en consecuencia para la ciencia física, por nombrar un ejemplo.
Podemos entonces afirmar que si quisiéramos entender cualquier tipo de movimiento (bien sea particular o combinado) realizado por un determinado móvil al menos de forma general siempre será necesario poder visualizar la descripción de su trayectoria, en donde, las distintas figuras geométricas juegan un esencial papel dándose de esta manera el más extraordinario nexo entre la cinemática y la geometría analítica.

La línea recta
Esta importante figura geométrica ha contribuido a la comprensión y desarrollo de innumerables actividades llevadas a cabo por la humanidad, así como en el entendimiento de distintos fenómenos que nos circundan día tras día durante el desenvolvimiento de nuestras vidas, y entre los cuales encontramos el reconocido fenómeno del movimiento en particular el movimiento rectilíneo.
Esta figura generalmente la relacionamos con la definición de la longitud cuando nos referimos a ella como la distancia más corta entre dos punto, sin embargo, la línea recta en términos de geometría analítica representa el lugar geométrico ocupado o formado por dos puntos distintos tales como P1(X1, Y1) y P2(X2,Y2) los cuales pertenecen a dicho lugar geométrico, teniendo en cuenta que el valor de su pendiente (m) podríamos calcularlo mediante la siguiente expresión:

Con la anterior descripción nos vamos familiarizando con la trayectoria recorrida por el movimiento rectilíneo, esto nos sigue permitiendo relacionar a estas dos grandes áreas de la ciencia, es decir, geometría analítica y cinemática, profundizando de esta manera en el estudio de los diversos movimientos de nuestro universo.
Por lo tanto, podríamos afirmar que la línea recta es una elemental figura para el análisis del movimiento en general, sobre todo en el movimiento rectilíneo, a continuación les dejo el enlace de una de mis publicaciones para que puedan seguir ampliando los conocimientos sobre esta magnífica figura geométrica como lo es la línea recta.
La circunferencia
Esta figura al igual que la línea recta, representan formas geométricas muy reconocidas por cualquiera de nosotros en especial por cualquier estudiante a diferente nivel académico, la circunferencia como ya hemos descrito en otras publicaciones relacionada con dicha figura, es el lugar geométrico en el cual un punto cualesquiera en el plano tiene movilidad pero a una distancia siempre constante a un punto fijo del mencionado plano y el cual lo llamamos centro (C), a la distancia descrita como constante es a la que conocemos con el nombre de radio (r), estos dos extraordinarios elementos en conjunto con las coordenadas polares son los encargados de dar forma a una trayectoria de tipo circular, como podemos observar en la siguiente figura 1.
Figura 1. Circunferencia trayectoria
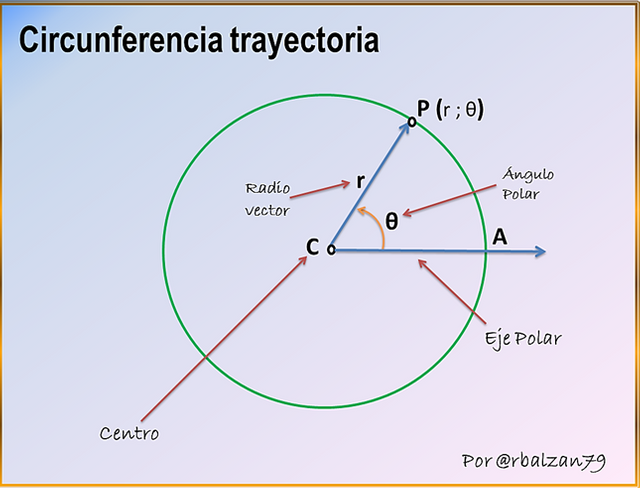
Una esencial figura que unida a la línea recta dan origen a una trayectoria combinada, es decir, rectilínea-circular de igual forma ampliando el rango para el análisis del movimiento por parte de la cinemática, para seguir profundizando sobre tal forma geométrica les dejo el enlace de una de mis publicaciones relacionada a la circunferencia.
La parábola
Figura geométrica de mucha relevancia para el estudio de diversos fenómenos de nuestro entorno y de la misma manera que la línea recta y circunferencia se consideran las tres elementales formas geométricas de gran utilidad para la formación académica de nuestros estudiantes, y de igual forma ampliamente conocidas en el amplio mundo tanto académico como científico debido a la descripción de sus lugares geométricos.
Por lo tanto, la parábola representa aquel espacio o lugar geométrico donde un determinado punto ubicado en un plano rectangular tiene movimiento de tal forma que la distancia a una recta fija llamada directriz será siempre igual a la distancia a un punto fijo llamado foco de dicha parábola, como podemos observar en la siguiente figura 2.
Figura 2. La Parábola y sus elementos más importantes
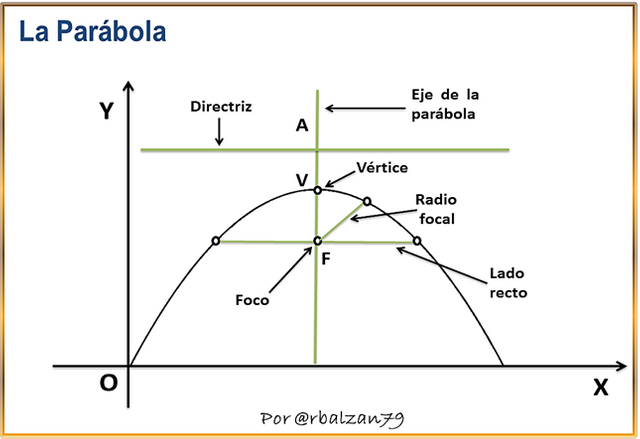
Otra esencial figura que unida a la línea recta y circunferencia pueden dar origen a una impresionante trayectoria combinada, es decir, recta-curvilínea aumentando aún más el rango para el análisis del movimiento a través de la cinemática, para profundizar sobre tal forma geométrica les dejo el enlace de una de mis publicaciones en relación a la parábola.

Movimiento rectilíneo
Este tipo de movimiento es posible observarlo a cada momento y en cualquier espacio de nuestras vidas, el mismo podríamos afirmar que representa la piedra fundacional del entendimiento sobre tal fenómeno, a pesar que por lo general los tipos de movimientos en nuestro entorno son curvilíneos.
El fenómeno del movimiento constituye para la ciencia física uno de los conceptos más esenciales debido a que su relación con nuestro medio natural es impresionantemente necesario y vital, como sabemos esta grandiosa ciencia se alimenta constantemente de nuestra naturaleza es por eso que cualquier relación de las distintas ramas del campo de la ciencia con lo natural siempre encontrará a la física como su mejor e imprescindible aliado, esto ya lo hemos visto con relación a la geometría.
Antes de llegar a este artículo realizamos por separado el análisis de cuatro importantes y vitales movimientos curvilíneos, los mismos fueron asistidos magistralmente por los espacios o lugares geométricos de las figuras denominadas cónicas representando de esta forma las diferentes trayectorias recorridas por cualquier partícula, cuerpo u objeto logrando de esta manera realizar el estudio del movimiento circular, parabólico, elíptico y el hiperbólico, en donde resaltamos el valioso papel que cada uno de ellos tienen en nuestro universo y en consecuencia en nuestras vidas.
Luego de los anteriores análisis le corresponde al movimiento rectilíneo mostrarnos sus características más allá de su propia comprensión y aplicación ya que se unirá a otros movimientos curvilíneos como el circular y parabólico mediante trayectorias combinadas y con ello resaltaremos una de las más grandes cualidades tanto de este tipo de movimiento rectilíneo como de la mente humana, debido a que el hombre a través de la ciencia ha logrado combinar distintos conocimientos incrementando exponencialmente su intelecto y calidad de vida.
En relación a lo antes expresado podríamos decir de forma general que una determinada partícula cuerpo u objeto puede desplazarse siguiendo un movimiento rectilíneo cuando en su trayectoria o recorrido describe el lugar geométrico de una línea recta.
La trayectoria recorrida como ya hemos expresado siempre nos permite ubicarnos en relación al tipo de movimiento realizado por cualquier cuerpo u objeto (móvil) a estudiar debido a que dicha trayectoria marcará la orientación y por lo tanto las formulaciones matemáticas a utilizar durante el análisis de un determinado movimiento.
Si nos ubicamos en nuestra realidad encontraríamos innumerables movimientos de tipo rectilíneo, una persona en un automóvil o en cualquier tipo de vehículo por lo general transita por una trayectoria rectilínea, o al caminar podríamos seguir una línea recta, un pícher o lanzador en un juego de béisbol en un determinado momento utilizará un lanzamiento llamado recta (sin darle efecto rotatorio a la pelota), en donde la pelota es lanzada con gran velocidad siguiendo la trayectoria del lugar geométrico de una línea recta, como podemos observar en el siguiente gif.
Gif representando un tipo movimiento rectilíneo.

Impresionantes ejemplos podríamos encontrarnos en nuestra cotidianidad con relación a dicho movimiento rectilíneo, sin embargo, su combinación o relación con otros tipos de movimientos lo hace aún más atractivo e impresionantemente útil para todos nosotros como veremos más adelante en los movimientos combinados.
La línea recta y el movimiento circular
La línea recta de forma general guarda una esencial relación con las distintas figuras geométricas, esto le permite jugar un importante papel en el estudio de los distintos movimiento de nuestro entorno y sin lugar a dudas en aquellos cuya trayectorias comprenden un sector o alguna representación lineal de forma por lo menos intrínseca como es el caso de la circunferencia y su esencial elemento como lo es el radio (r), cuya longitud esta expresada geométricamente por una línea recta y en el movimiento circular mediante el radio vector (característica de orientación aportada por la geometría analítica) podríamos lograr la ubicación de cualquier partícula cuerpo u objeto que transita por el espacio geométrico de una determinada circunferencia llevándose a cabo el movimiento circular.
Aunque en el ejemplo mencionado la línea recta no se combina con la trayectoria circular su utilización para el análisis de dicho movimiento es importante ya que la posición de la partícula, cuerpo u objeto forma parte esencial para el estudio del movimiento en general.
Un ejemplo práctico el cual relaciona la línea recta con un movimiento circular es representado por las órbitas geoestacionarias, este tipo de órbita es reconocida por el hecho de mantener a ciertos satélites artificiales en sincronía con el planeta tierra mediante un movimiento circular, es decir, que los mismos giren de forma sincronizada con nuestro planeta para lo cual se debe tener en cuenta tanto la velocidad de escape como la altura (h) necesaria para este tipo de órbita y de esta forma dichos satélites puedan permanecer siempre unido en el mismo punto con la tierra.
En relación a la altura requerida por esta órbita podríamos decir que es la distancia existente entre un punto cualesquiera de nuestro planeta con un punto en el espacio o lugar geométrico de la circunferencia trayectoria de dicha movimiento circular, el cual representará la órbita geoestacionaria, al unir estos puntos obtendríamos la figura de un línea recta la cual representaría la forma geométrica de la altura requerida para una órbita geoestacionaria en conjunto con la obtención de los datos de la velocidad de escape, ya que esta última determinará el tipo de órbita de cualquier partícula, cuerpo u objeto lanzado al espacio como es el caso de los satélites artificiales, a continuación presentamos un gif el cual representa una órbita geoestacionaria.
Gif de una órbita geoestacionaria

Como hemos podido notar la línea recta se encuentra inmersa en innumerables análisis o estudios de grandiosos fenómenos o actividades relacionadas con nuestra cotidianidad en donde el movimiento siempre ha sido parte esencial de nuestra existencia.
Movimiento rectilíneo-circular
Este maravilloso movimiento de trayectoria combinada nos permite incrementar la gran utilidad de los distintos tipos de movimientos existente de manera individual, cualquier persona es testigo fidedigno de esta clase de movimiento rectilíneo-circular o viceversa debido a que el mismo lo podemos llevar a cabo sin mucho o ningún esfuerzo en cualquier momento o también podemos observarlos, el ser humano ha logrado diseñar gran cantidad de elementos utilizados o implementados en diversas actividades con la finalidad de realizar algún tipo de trabajo con más facilidad y en consecuencia con un menor esfuerzo.
Podemos entonces referirnos a los distintos mecanismos empleados para la transmisión de un movimiento como el rectilíneo-circular o viceversa, por lo tanto, podemos de esta manera transferir y convertir fuerzas y movimientos desde de un determinado elemento motriz (motor) hacia un elemento receptor.
Un palpable ejemplo de este tipo de movimiento podríamos decir que lo representa la simple actividad de enroscar una tuerca en un tornillo, mediante este ejercicio podemos ver claramente que a medida que la tuerca gira o realiza un movimiento circular esta se desplaza simultáneamente en una trayectoria recta, este es el principio fundamental del fenómeno del movimiento en todas sus características poder formar parte de cualquier actividad del ser humano por muy simple que parezca.
Otro ejemplo lo podríamos observar mediante el movimiento circular realizado por un determinado piñón sobre una cremallera, originándose de esta manera la transformación de un movimiento circular en una lineal, este último representado por el movimiento de la cremallera, como podemos observar en la siguiente figura 3.
Figura 3. Transformación del movimiento circular en uno rectilíneo
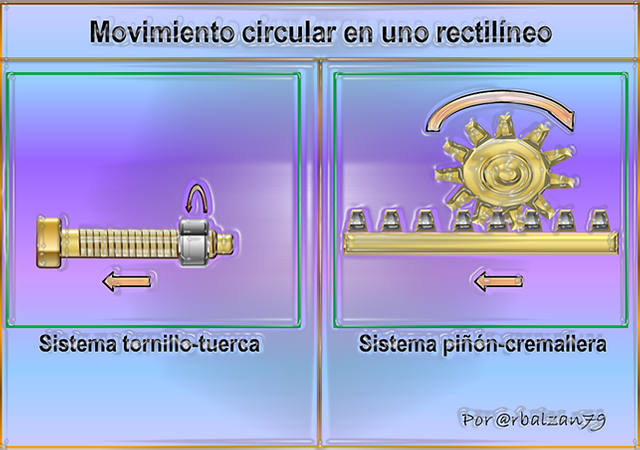
Innumerables son los ejemplos de este tipo de movimiento que sin duda la humanidad lo lleva a cabo con gran naturalidad que ni cuenta se da al momento de llevarlo a cabo.
Movimiento rectilíneo-parabólico
Este tipo de movimiento de igual forma lo podemos llevar a cabo de una forma práctica como también visual ya que en muchas ocasiones nos trasladamos en un automóvil o cualquier tipo de vehículos por una determinada autopista o carretera en donde cuya trayectoria por lo general es recta con gran cantidad de trayectos en donde notamos que subimos y bajamos, es decir, con elevaciones debido a que estas vías son construidas sobre algunas montañas y áreas planas o planicies coincidiendo de esta forma con trayectorias de tipo rectilíneas-parabólicas, como observamos en la siguiente figura 4.
Figura 4. Trayectoria combinada Rectilínea-parabólica
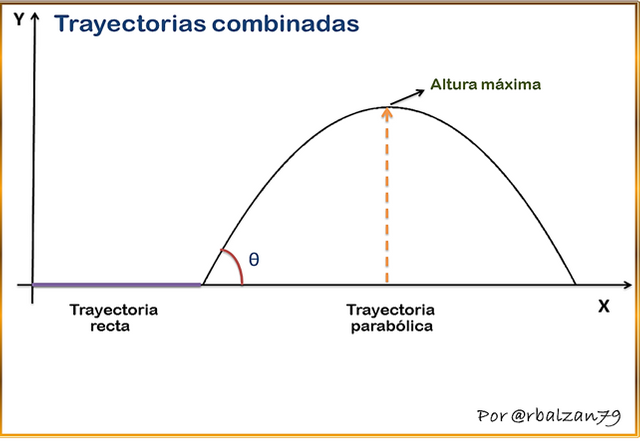
Es importante poder resaltar que un movimiento parabólico es posible estudiarlo mediante la unión de dos tipos de movimientos rectilíneos relacionando de esta forma a estos dos tipos de movimientos como el rectilíneo y el parabólico, y a pesar de no ser una combinación de trayectorias por medio del movimiento rectilíneo es posible analizar uno parabólico.
De esta manera considerando la trayectoria de una determinada partícula, cuerpo u objeto con movimiento parabólico y con proyección en el eje de las X, el cual se encuentra paralelo a la superficie terrestre observaremos como describe sobre tal eje un movimiento rectilíneo uniforme, esto si observamos dicho movimiento desde una mirada aérea, es decir, en el mismo plano vertical de dicha trayectoria.
Si observáramos dicho movimiento parabólico proyectado sobre el eje de la Y, podríamos ver como si el cuerpo o partícula se elevara y cayera verticalmente describiendo de esta manera un movimiento rectilíneo uniformemente acelerado y cuya aceleración estaría representada por la acción de la gravedad, este recorrido lo notaríamos al estar en el suelo de frente y en el mismo plano vertical de la trayectoria del lanzamiento (a una distancia considerable del disparo) que describe el mencionado movimiento parabólico, a continuación les mostramos un gif el cual representa un movimiento rectilíneo-parabólico.
*** Gif movimientos con trayectorias combinadas rectilíneo-parabólica.***

Movimiento rectilíneo-parabólico-circular
En relación a este tipo de movimiento encontramos la combinación de tres diferentes trayectorias representadas por el lugar geométrico de las figuras tales como la línea recta, la parábola y la circunferencia, originándose de esta forma también el extraordinario nexo entre los movimientos rectilíneos, parabólicos y circulares como lo podemos ver y en muchos caso disfrutar en algún parque de diversión a través de las denominadas montañas rusas, en donde podemos encontrar esta magnífica combinación de trayectorias y por tanto de los movimientos antes señalados como observamos en la siguiente figura 5.
Figura 5. Trayectoria combinada (Rectilínea-parabólica-circular)
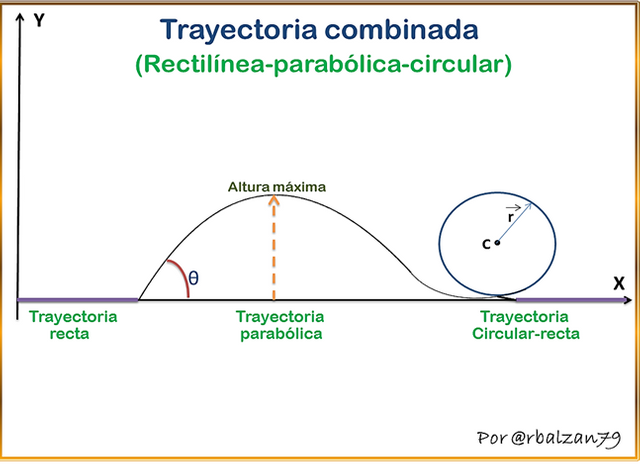
Es impresionante poder observar o disfrutar del recorrido de este tipo de trayectoria en el caso antes planteado como en el gif al inicio de esta publicación, pero son muchas las actividades del ser humano en donde la utilidad de este tipo de movimiento es de gran valía, por lo tanto, la combinación de movimientos nos ha permitido o facilitado muchas de nuestra labores o actividades en las distintas áreas que envuelven nuestra existencia.

Muchos son los modelos matemáticos utilizados para complementar el lenguaje universal del fenómeno del movimiento en sus distintos aspectos o características, en esta oportunidad conoceremos y recordaremos algunos modelos matemáticos específicos implementados durante el análisis de algún tipo de movimiento y de la misma forma aquellos modelos relacionados con las diferentes trayectorias que recorren toda partícula, cuerpo u objeto a través de los lugares geométricos de importantes figuras como la parábola, circunferencia y línea recta, permitiéndonos establecer y relacionar tantos las trayectorias como tipos de movimientos respectivamente.
Trayectoria recta-curvilínea
Es importante relacionar a estas figuras geométricas sobre todo conocer aquellos modelos matemáticos que nos permiten dibujar sus trayectorias ya que a través de las mismas nos hemos apoyados en cualquier tipo de complementariedad de algún tipo de conocimiento como lo hemos podido demostrar en el desarrollo de este artículo, por lo tanto, iniciaremos con aquellas formulaciones relacionadas con la trayectoria de una línea recta.
Trayectoria rectilínea
Una determinada trayectoria lineal desde el punto de vista geométrico la podríamos establecer al conocer las coordenadas de uno de sus puntos y su respectivo ángulo de inclinación y con este último dato obtendríamos su pendiente (m), por lo tanto, conocidas las coordenadas de uno de los puntos de la recta y su pendiente la formulación que representaría estas condiciones sería la siguiente:

De igual forma conociendo dos puntos de dicha recta tenemos la siguiente expresión o fórmula:

Trayectoria parabólica
Tomando en cuenta la trayectoria de la parábola en un plano cartesiano rectangular como de igual forma se realiza para las distintas trayectorias de cualquier figura geométrica en dos dimensiones, y en donde para este caso dicha trayectoria parabólica tiene su vértice en el origen y su eje focal coincide con cualquier eje coordenado del plano rectangular, por lo tanto, tomaremos en cuenta que el vértice de la parábola se encuentra en el origen (0,0) y su eje focal coincide con el eje de las X, la formulación para estas condiciones es la siguiente:

Para el caso en donde el vértice siga en el origen y el eje focal coincida ahora con el eje de las Y, esta trayectoria estará representada por la siguiente ecuación:

Trayectoria circular
Para representar este tipo de trayectoria tomando en cuenta que el centro (C) de la circunferencia tiene como coordenadas (h , k) y cuyo radio (r) es constante, utilizamos la siguiente formulación matemática:

En el caso cuando el centro de una circunferencia trayectoria se encuentre en el origen de un plano cartesiano rectangular tendríamos que h = k = 0, por lo tanto, la ecuación a utilizar sería la siguiente:

La cinemática en trayectorias combinadas
Esta impresionante ciencia del movimiento constantemente se ha alimentado de extraordinarias formulaciones matemáticas con la finalidad de dar respuesta a tantas interrogantes relacionadas sobre los distintos tipos de movimientos los cuales se llevan a cabo en nuestro tan movido entorno, poder analizar un movimiento en particular es realmente fascinante debido a su amplísima aplicación entre nosotros, ahora poder estudiar y describir la utilidad del nexo de varios movimiento eleva exponencialmente sin duda su ejemplar aporte para nuestro desarrollo en todos los sentidos.
Es importante tener en cuenta que podríamos tener visualizadas las trayectorias de un determinado recorrido de una partícula, cuerpo u objeto pero debe darse precisamente tal recorrido por dichas trayectorias para que puede existir algún tipo movimiento, cuando esto ocurre es en donde la cinemática se presenta con su amplia capacidad de interpretación del fenómeno del movimiento conjuntamente con aquellas trayectorias extraídas de destacables figuras geométricas ofrecidas por la geometría analítica.
Ambas ciencias (cinemática - geometría analítica) han logrado sus objetivos gracias a las distintas formulaciones matemáticas, es decir, el lenguaje más universalmente posible con que cuenta la humanidad alcanzando así de manera efectiva la transmisión de tales conocimientos hacia las distintas áreas de nuestro desarrollo intelectual y sin duda social.
En el recorrido de trayectorias combinadas rectilíneas-curvilíneas conoceremos algunas formulaciones matemáticas imprescindibles para la comprensión de los movimientos involucrados en esta asociación de trayectorias iniciando con aquellas expresiones relacionadas con el movimiento rectilíneo.
Formulaciones matemáticas para el movimiento rectilíneo
El movimiento rectilíneo como lo expresamos es aquel realizado por cualquier partícula, cuerpo u objeto (móvil) cuya trayectoria es el lugar geométrico de una línea recta, hasta ahora hemos conocidos algunas formulaciones o expresiones matemáticas especificas desde el punto de vista de su trayectoria, pero es necesario complementarlas con aquellas expresiones o ecuaciones que relacionen también el recorrido o movimiento de dicho móvil, para ello iniciaremos con el tipo de movimiento rectilíneo más sencillo.
Movimiento rectilíneo uniforme (MRU)
Para este caso el móvil se desplazará en línea recta y principalmente siempre a una velocidad constante, es decir, conservando tanto la misma intensidad como la dirección y sentido.Es importante tener en cuenta que dicho movimiento debamos tomarlo en cuenta en una sola dimensión, esto con el objetivo de facilitar su análisis por lo que es conveniente seleccionar un punto de referencia ubicado sobre la recta que representa la trayectoria y sobre esta hacer descansar el eje X, de esta forma nos aseguramos que todas aquellas magnitudes vectoriales, tales como velocidad, posición y desplazamiento las encontremos sobre la misma recta con el propósito de facilitar las interpretaciones o formulaciones matemáticas.
Para este caso de movimiento lineal la posición instantánea de un móvil queda definida claramente con la coordenada X, la cual nos informará la longitud o distancia al origen y el signo nos indicara de qué lado o posición del origen estará el móvil, como para este tipo de movimiento la velocidad es constante descartamos la interpretación de velocidades como instantánea, inicial, final o promedio ya que esta siempre será igual.
Movimiento rectilíneo uniformemente acelerado
Por lo general todos los movimientos presentes en nuestra cotidianidad su velocidad no la representa una magnitud constante y por lo tanto la aceleración estará siempre presenta bien sea por causas naturales como la representada por la acción gravitatoria o por otras razones o interacciones tales como el rozamiento, la fuerza ejercida por un motor u otros elementos o mecanismos diseñados por el hombre.
Para poder comprender este tipo de movimiento en forma general se considera influenciado por la acción natural de la gravedad con la finalidad de observar con mayor facilidad el cambio de la velocidad y el desplazamiento de cualquier móvil que realice este movimiento, de esta forma cualquiera de nosotros podríamos notar que al soltar algún objeto desde una determinada altura el mismo caerá y si lo arrojamos hacia arriba desde el suelo de igual forma describirá dicho objeto una línea recta proyectada en el eje vertical (como el mencionado ejemplo en relación con el movimiento parabólico) pero no lo hará con movimiento rectilíneo uniforme ya que se trata de un movimiento rectilíneo uniformemente acelerado cuya aceleración es constante y representada generalmente por la gravedad o según sea el tipo de fuerza que actúa sobre el móvil.
Para este tipo de movimiento lineal según sea las características a estudiar o analizar se utilizan las siguientes formulaciones o ecuaciones matemáticas:

Una vez conocidas ciertas formulaciones matemáticas sobre el movimiento rectilíneo ahora recordaremos las ecuaciones más relevantes en el estudio de los movimientos tanto circulares como parabólicos los cuales representan en esta oportunidad los tipos o clases de movimientos curvilíneos en tal combinación de trayectorias.
Formulaciones para el movimiento circular
Este movimiento representa un importante fenómeno particular para todos nosotros debido a que forma parte tanto de nuestro entorno como de nuestras actividades cotidianas, por lo que en resumen podríamos decir que el mismo representa un tipo de movimiento curvilíneo debido a que recorre la trayectoria de una circunferencia y lo hace con una velocidad y con un respectivo ángulo en su recorrido, por lo cual se denomina velocidad angular (ω), esta velocidad no es más que el número de vueltas que un determinado móvil efectúa por unidad de tiempo, por lo que la misma está representada por la siguiente ecuación:

De esta forma encontramos otras extraordinarias formulaciones para este tipo de movimiento por lo que invitamos a los amigos lectores a conocer más sobres dichas ecuaciones a través del siguiente enlace, en donde se realizó el análisis particular del movimiento circular.
Formulaciones para el movimiento parabólico.
Ahora nos encontramos con otro importante movimiento curvilíneo como lo es el movimiento parabólico y el cual de la misma forma que otros movimientos en particular cuenta con modelos matemáticos específicos y necesarios para poder entenderlo a través de un lenguaje universal como lo es el álgebra implementada en la geometría analítica, por lo tanto tomando en cuenta su recorrido por una curva la cual describe un ángulo tenemos algunas de sus importantes formulaciones:
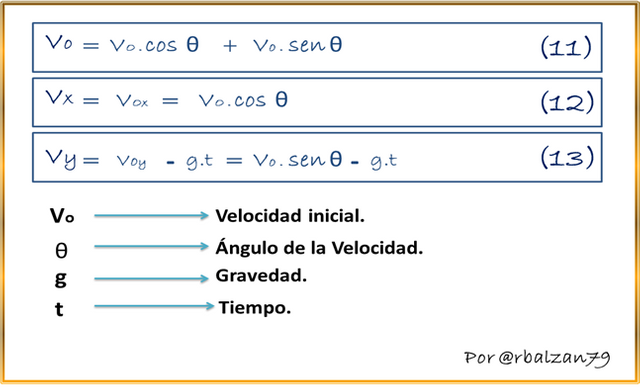
También encontramos otras extraordinarias formulaciones para este tipo de movimiento parabólico, por lo que invitamos nuevamente a los amigos lectores poder conocer más sobres dichas expresiones a través del siguiente enlace, en donde se realizó el análisis particular del movimiento parabólico.
De esta manera conocimos algunas expresiones o ecuaciones matemáticas específicas para cada caso de movimiento y las cuales de igual forma podríamos fácilmente utilizarlas en el caso de trayectorias recorridas de forma combinadas, realizando el análisis sectorialmente dependiendo de los distintos tipos de trayectorias mezcladas con la finalidad de un determinado propósito o actividad realizada por la humanidad.

1.- La ciencia física a lo largo de su historia ha hecho de nuestro mundo un hogar verdaderamente dotado de características naturales trasmitidas hacia nuestras actividades cotidianas, debido a que esta ciencia además de estudiar los distintos fenómenos a través de la observación y sus análisis teóricos ha podido traducirlos en un maravilloso lenguaje universal con la ayuda de la ciencia matemática específicamente a través de una de sus más fructífera rama como lo es la geometría analítica, ya que la misma como sabemos cuenta con el maravilloso lenguaje abstracto del algebra y en consecuencia dotándonos de espectaculares figuras y formulaciones matemáticas.
2.- Respecto al maravilloso fenómeno del movimiento cualquiera pudiese pensar que ha sido tarea fácil llegar hasta donde hemos llegado en cuanto a su entendimiento, sin embargo, esta tarea a través del espacio-tiempo no ha resultado nada fácil y es por eso que siempre debemos resaltar la extraordinaria labor de la ciencia del movimiento como lo es la cinemática, esta ha buscado a lo largo de su incansable estudio distintos nexos los cuales les permitiera resolver los innumerables enigmas que encerraban las acciones de tal fenómeno encontrando en su camino a la esencial ciencia de las formas y las figuras, es decir, la geometría analítica, a partir de ese momento los pasos dados han sido agigantados brindándonos hasta la actualidad todo lo que conocemos sobre el fenómeno del movimiento.
3.- Si observáramos con detenimiento todo aquello que nos rodea tanto en el aspecto natural como todo aquello diseñado por el hombre veríamos impresionantes movimientos bien sea de manera singular o plural, y al seguir cada recorrido podríamos describir visual y analíticamente cada una de las trayectorias recorridas, por lo tanto, fácilmente dibujaríamos con nuestra imaginación tales figuras geométricas, es decir, notaríamos como todo aquellos que nos rodea está representado por la ciencia geométrica analítica y estudiada por la ciencia física.
4.- Podríamos afirmar en términos generales que el movimiento rectilíneo representa la piedra fundacional para el entendimiento de este fenómeno de forma global, dicho movimiento hace uso del lugar geométrico de una línea recta en su recorrido.
Cualquiera de nosotros poder observar un determinado movimiento llevado a cabo por un móvil siempre será un enorme placer, sin embargo, poder realizar o sentir el recorrido de un movimiento bien sea particular o combinado eleva aún más el grado de satisfacción para cualquier ser humano que tenga la oportunidad de vivirlo, y es para eso que el hombre ha trabajado tanto con la finalidad de sacar el mayor provecho a cada uno de los conocimientos adquiridos y aumentar de esta manera tanto el tiempo de sobrevivencia en este planeta como elevar nuestro nivel de vida.
5.- Para concluir mis amigos y apreciados lectores como lo he expresado en las anteriores publicaciones, la geometría analítica con la cinemática representan un claro ejemplo de enseñanza para todos nosotros sin distinción de clase, raza o credo, y a pesar de ser muy complejas por tratar de entender nuestra naturaleza claro está, son realmente grandiosas debido a que ellas al igual que es resto del campo científico nos han brindado todo nuestro intelecto y estabilidad social en forma general.
Hasta otra oportunidad mis apreciados lectores de steemit, en especial a los miembros de la gran comunidad de #STEM-Espanol, los cuales reciben el apoyo de otras tres grandes comunidades como los son #steemstem, #utopian-io y #curie, por lo cual recomiendo ampliamente formar parte de este hermoso proyecto, ya que resalta la valiosa labor de la academia y del campo científico, pero sobre todo, por el gran respecto, dedicación y ayuda para sus miembros.
Nota: Todas las imágenes fueron elaboradas usando las aplicaciones Paint, Power Point y los gifs con la aplicación de PhotoScape, el gif relacionado con la órbita geoestacionaria se utilizó un porción de una imagen de dominio público extraída de Pixabay.com Fuente.

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.
[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.
[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.
[4] Gómez Ana Inés. Órbitas en el sistema solar, Volumen 3. Facultar de ciencias matemáticas, Universidad Complutense de Madrid.
[5] O. Montebruck, E. Gill. Órbitas de satélites.
[6] Bragado Ignacio Martin. Física General. [email protected] .12 de febrero de 2003.
[7] Alegría Pedro. Las cónicas y sus aplicaciones.pedro.alegrí[email protected].
[8] Prieto Santiago, Rodríguez, Silveira Ismael. Física General 1. Universidad de la República; Instituto de física, Facultad de ingeniería - UdelaR, 2007.
[9] Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5ta edición. Tomo I. McGraw-Hill.
[10] Arroyave Valencia, Carlos. Movimiento Parabólico. Instituto Técnico Industrial Pascual Bravo.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias amigos por su constante apoyo. Saludos.
Gracias a toda la comunidad de cervantes en especial a @ramonycajal por su valioso apoyo. Saludos.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks to the communities of @SteemSTEM, @ utopian-io and @curie for the support received.
Congratulations @rbalzan79! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Hi @rbalzan79!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks for your valuable support. Greetings.