En primer lugar mis saludos respetuosos para toda la comunidad de steemit, continuando con la temática geometría analítica plana, en donde seguimos dando importantes pasos para la comprensión analítica de las matemáticas, en esta oportunidad estudiaremos a la circunferencia, por lo tanto, conoceremos su ecuación en su forma ordinaria y forma general, con esto seguimos con el análisis detallado de las ecuaciones y los lugares geométricos de una curva específica, determinando de esta manera sus propiedades particulares.

En la pasada publicación analizamos a la línea recta, ahora como ya describimos analizaremos a la circunferencia, la cual representa después de la línea recta, una de las curvas más familiares para los estudiantes y personas en cualquier área profesional.

Ecuación de la circunferencia; en su forma ordinaria

Desde el punto de vista de la geometría analítica plana, podríamos expresar que la circunferencia es aquel lugar geométrico, en donde, un determinado punto tiene movilidad en el plano cartesiano de tal forma que se mantiene a una distancia siempre constante de un punto fijo del respectivo plano, y que dicho punto fijo lo llamaremos o conoceremos como centro (C) de la circunferencia, y que a dicha distancia constante la denominaremos radio (r), por lo tanto, en pocas palabras podemos expresar que la ecuación de una circunferencia cuyo centro tiene como coordenadas (h , K) y que además conociendo que su radio es constante (r), tiene la siguiente expresión:

En la siguiente figura podemos observar lo antes planteado, para la determinación de dicha expresión o ecuación de la circunferencia.

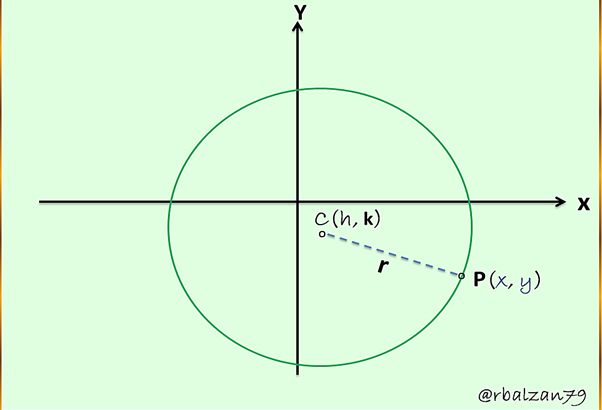
Por lo tanto, el punto P junto al centro (C) debe cumplir con la siguiente condición:

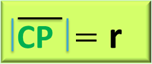
En donde mediante la fórmula para la distancia entre dos puntos en el plano ya conocida por nosotros con anterioridad, podemos demostrar analíticamente el planteamiento para la ecuación de la circunferencia en su forma ordinaria, por lo tanto, tenemos lo siguiente:

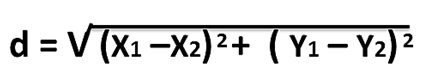
En donde, al simplificar la raíz nos queda la expresión:

Esto lo podemos aplicar a cualquier punto que se desplace a una distancia constante de un determinado centro, originando de esta manera la curva o espacio geométrico de una circunferencia.

Es importarte resaltar, cuando el centro de una circunferencia se encuentra en el origen del plano tenemos que tanto h = k = 0, por lo que su ecuación se reduce a la siguiente expresión:

Esta expresión en muchas de las ocasiones la encontraremos con el nombre de forma canónica, debido a que representa el ejemplar más sencillo de la ecuación de una curva, en este caso para la circunferencia.

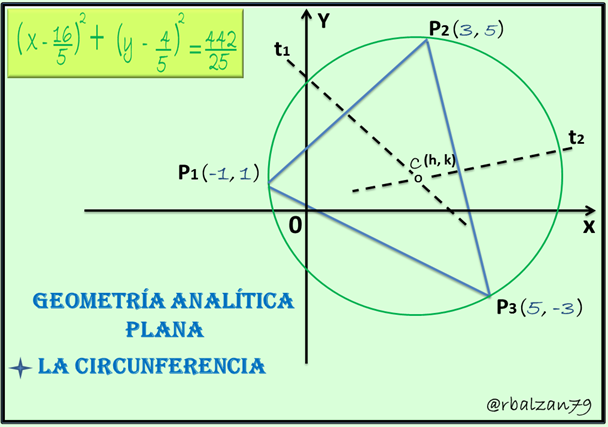
Ejercicio 1

Hallar la ecuación de la circunferencia la cual se encuentra circunscrita a un triángulo cuyos vértices son los puntos P1(-1 , 1) , P2(3 , 5) , P3(5 , -3), como se muestra en la siguiente figura:

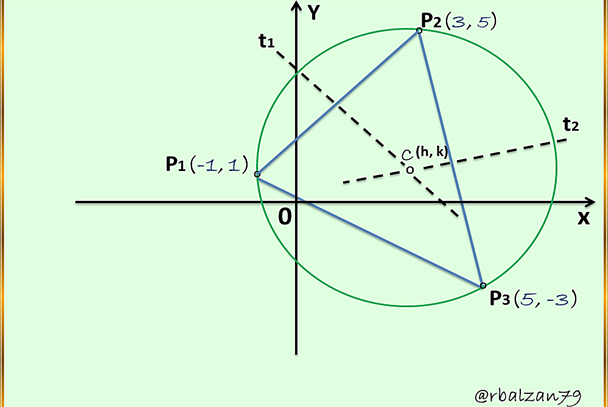
Para cumplir con las características antes mencionadas, nos apoyamos en el método de la construcción de mediatrices de los lados del respectivo triángulo, trabajaremos con al menos dos de estos lados, y denominaremos t1 y t2 a sus respectivas mediatrices, estos lados pudieran ser P1P2 y P2P3, en donde, la intersección de estas dos rectas (mediatrices) representará el centro (C) de la circunferencia, y por lo tanto, la distancia del centro (C) a cualquiera de estos tres puntos dados o vértices del triángulo será nuestro radio (r), entones, empecemos con nuestra tarea hasta llegar a la determinación de la ecuación de la circunferencia, por lo tanto, tenemos:

Determinaremos las ecuaciones de las rectas o mediatrices antes descritas, con la finalidad de realizar sus gráficas y encontrar su punto de intersección y con ello nuestro anhelado centro de circunferencia.

Sabemos por los distintos métodos analizados en la determinación de la ecuación de una línea recta que al conocer un punto de la misma y su pendiente podemos confeccionar su ecuación, entonces, para t1 del lado P1P2:

Identificamos las coordenadas del punto medio (M) del segmento, para ello recordamos lo siguiente.

Ahora sustituimos:

Ahora buscamos las pendientes de cada uno de estos lados, dichos lados representan los segmentos de una recta, por lo tanto, conocemos dos puntos para obtener dichas pendientes:

Luego de obtener ambas ecuaciones de las rectas (mediatrices), procedemos a despejar de una de ellas a (x) en función de (y) para sustituir en la otra ecuación y después a (y) en función de x, para encontrar las coordenadas del centro de la circunferencia.

Ahora conocemos con estas coordenadas el centro (C) de la circunferencia, con este punto C y con cualquiera de los tres puntos dados podemos encontrar el radio:

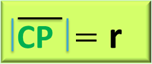
Forma general de la ecuación de la circunferencia

Para este caso conocemos la forma ordinaria de la ecuación de la circunferencia:

En donde al desarrollarla nos queda de la siguiente manera:

La misma podemos escribirla de la forma siguiente:

Para lo cual:

Por lo tanto, una determinada ecuación de la circunferencia es posible expresarla en la forma general antes planteada, pero debemos verificar la reciprocidad, es decir, si cualquier ecuación en forma general puede representar una determinada circunferencia, para ello, cuando queramos comprobar lo antes expresado pasamos de la forma general a la ecuación ordinaria de la misma, es decir, como sigue a continuación:

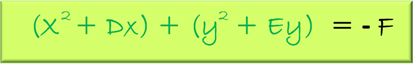
Ejercicio 2

Reducir la siguiente ecuación general a la forma ordinaria de la ecuación de la circunferencia, si la misma representa a una circunferencia encontrar su centro y radio.

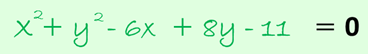
Aquí podemos recomendar la utilización del método de completar cuadrados, que nos permita colocar nuestra ecuación general de la siguiente forma ordinaria:

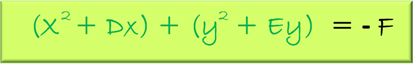
Entonces, procedamos a la aplicación del método antes mencionado, para ello organizamos nuestras variables iniciando con las que tienen x, luego las de y, después nuestro término independiente:

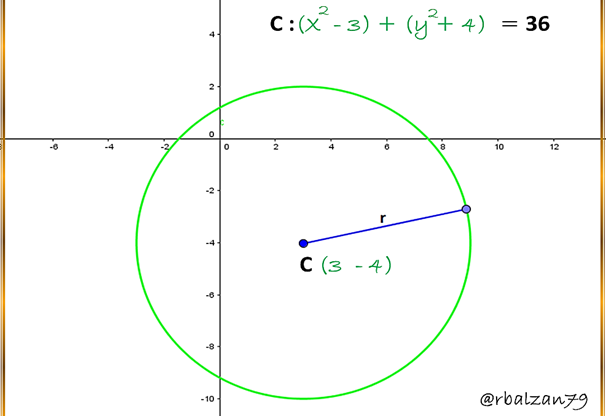
Con la ayuda de GeoGebra, mostramos la representación gráfica de la ecuación de nuestra circunferencia:

Conclusiones

1.- Por lo general denominamos ecuación ordinaria de una curva, aquella que nos permite obtener de forma sencilla y rápida las características más importantes de la curva a la cual pertenece dicha ecuación, para este caso, como pudimos observar mediante la ecuación ordinaria de la circunferencia es posible obtener rápidamente las coordenadas tanto de su centro como de su radio.

2.- Es importante resaltar la relación entre circunferencia y círculo, debido a que en ocasiones algunas personas tienden a confundirlas, por lo que llamaremos circunferencia al conjunto de puntos en un plano cartesiano los cuales están a una distancia igual al radio (r), y este parte del centro de dicha circunferencia, mientras que el círculo representa al conjunto de una determinada circunferencia, es decir, todos los puntos interiores de la misma, por lo tanto, geométricamente, una circunferencia siempre será una línea; mientras que el círculo es una superficie.

3.- En el desarrollo de esta publicación pudimos utilizar los conocimientos de la línea recta, la cual, siempre representará la base fundamental para la comprensión de cualquier tipo de curva, y ahora con la circunferencia, podemos ampliar nuestras herramientas para la determinación de las ecuaciones de otras curvas, por lo tanto, seguiremos estudiando dichas curvas para la consolidación de tan importantes y necesarios conocimientos en el ámbito académico y profesional.

Nota: Todas las imágenes fueron elaborados usando las aplicaciones Paint, Power Point y GeoGebra.

Referencias Bibliográficas

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.

[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.

[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.

Autor: @rbalzan79