En primer lugar mis saludos respetuosos para toda la comunidad académica y científica de steemit, en especial a #stem-espanol, #steemstem, #utopian-io, #cervantes y #entropia, su valioso apoyo hace posible nuestro crecimiento en todos los aspectos en esta prestigiosa plataforma.

Continuando con la temática geometría analítica plana, en donde, continuamos fortaleciendo el aspecto analítico de las matemáticas, en esta oportunidad extendemos el análisis entre el maravilloso nexo de la grandiosa ciencia física y las matemáticas, esta última representada por la geometría analítica, por lo tanto, seguimos describiendo algunos de tantos elementos fundamentales que unen a ambas ramas científicas, como lo hemos comprobado en la primera, segunda y tercera parte de este esencial nexo mediante el movimiento circular , el movimiento parabólico y el movimiento elíptico.

Este análisis lo iniciaremos con la descripción geométrica de la importante figura llamada hipérbola debido a que la misma representa la trayectoria del fenómeno denominado movimiento hiperbólico, por lo que esta figura juega un papel imprescindible para el análisis del mencionado fenómeno, en donde como ya sabemos el estudio y comprensión del movimiento lo lleva a cabo la ciencia Física por medio de la cinemática.

En esta oportunidad seguimos afirmando que el objetivo principal de este artículo es resaltar el maravilloso y necesario nexo entre las dos más grandes ciencias de la humanidad, es decir, física y la matemática.

Como hemos podido notar y comprobar en los otros movimientos, la física tiene y tendrá la capacidad de nutrirse de sus propias ramas, en donde la cinemática representa un claro ejemplo ya que habernos brindado el entendimiento de los distintos tipos de movimiento ha sido realmente determinante para nuestra evolución.

Si cualquiera de nosotros quisiéramos entender el fenómeno del movimiento de forma general necesario siempre será poder visualizar la descripción de su trayectoria o recorrido, como ha sido el caso de los movimientos de tipos circulares, parabólicos y elípticos los cuales cada uno de ellos han recorrido los lugares geométrico de diferentes figuras cónicas como la circunferencia, parábola y elipse respectivamente, esto es lo que nos ha permitido descifrar la comprensión sobre este hermoso fenómeno, por lo tanto al analizar el movimiento hiperbólico de igual forma tenemos que observar la descripción de su trayectoria la cual se encuentra representada por el lugar geométrico de la cuarta forma cónica, es decir, la hipérbola.

La geometría analítica con su lenguaje abstracto, formas y figuras al igual que nuestro universo siempre estarán en una constante revisión tanto conceptual como experimental lo que nos permitirá seguir uniendo a la ciencia física con las matemáticas desde una visión claramente geométrica.

La hipérbola

Esta importante figura geométrica ha hecho posible la comprensión del movimiento hiperbólico el cual se encuentra en varios aspectos de nuestra naturaleza como es el caso de varios cuerpos celestes o astronómicos de nuestro universo, entre otros casos de importante valor para el estudio de fabulosos comportamientos de ciertos cuerpos o partículas que describen en su recorrido tal trayectoria de forma hiperbólica, por lo tanto podemos decir que dicha figura representa el lugar geométrico creado por el movimiento de un punto del plano rectangular coordenado, en el cual el valor absoluto de su diferencia o resta de las distancias a dos puntos fijos denominados focos es siempre la misma, por lo tanto una cantidad constante, positiva y además menor que la distancia focal, es decir, la distancia existente entre dichos puntos fijos (focos).

Descrito su aspecto conceptual es necesario poder conocer los elementos que constituyen esta forma geométrica como se muestra a continuación en la figura 1.

Figura 1. Elementos que conforman una hipérbola.

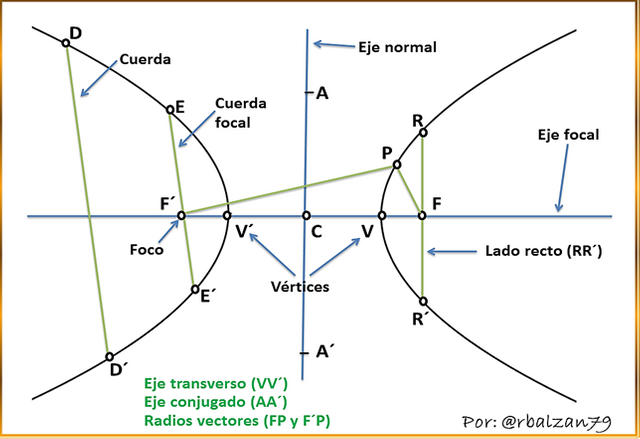
Con la anterior figura 1, nos vamos familiarizando con la descripción de la trayectoria o recorrido del movimiento hiperbólico, permitiéndonos seguir relacionando a estas dos áreas de la ciencia (geometría analítica y cinemática) en el estudio de los diversos movimientos de nuestro universo.

Una elemental figura para el análisis del movimiento hiperbólico realizado por la cinemática, es decir, la ciencia del movimiento, a continuación les dejo el enlace de una de mis publicaciones para que puedan ampliar más sobre esta magnífica forma geométrica como lo es la hipérbola.

Movimiento hiperbólico

El maravilloso fenómeno del movimiento ha dejado sus impactantes huellas en la humanidad, ya que sin su entendimiento y comprensión nuestro fabuloso desarrollo intelectual y social sería sin dudas mucho más bajo o aún más no hubiésemos logrado ser la especie viviente que somos hoy en día.

Entonces, podríamos afirmar que dicho fenómeno forma y formará parte de nuestra existencia y que gracias al extraordinario campo de la ciencia hemos sabido transmitir el lenguaje del movimiento a cualquier persona de este planeta con el firme propósito de mejorar nuestras vidas.

Antes de llegar a este artículo realizamos el análisis de tres importantes y vitales movimientos curvilíneos como lo son el circular, el parabólico y el elíptico, en donde destacamos el valioso papel que cada uno de ellos tienen en nuestro universo y por tanto en nuestras vidas, en esta oportunidad le corresponde al movimiento hiperbólico mostrarnos sus características e importancia entre todos nosotros.

De acuerdo a lo antes mencionado podríamos expresar de forma general que un determinado cuerpo, móvil o partícula puede desplazarse siguiendo un movimiento hiperbólico cuando en su trayectoria o recorrido describe el lugar geométrico de una hipérbola, en donde es importante resaltar desde el punto de vista de la geometría analítica el esencial elemento de excentricidad y el cual caracteriza a cada una de estas figuras cónicas como las estudiadas anteriormente, es decir, circunferencia, parábola y elipse dando origen de esta manera a una gran variedad y casi la totalidad de los tipos de movimientos del universo.

Un tipo de movimiento hiperbólico desde el punto de vista de la astronomía (mecánica celeste) es aquel descrito por un determinado cuerpo o partícula el cual escapa de la atracción gravitatoria de un determinado cuerpo central( representando dos claros ejemplos de cuerpos de fuerzas centrales, el Sol para nuestro sistema planetario y el planeta tierra para la luna y satélites artificiales) y de acuerdo a la teoría newtoniana la órbita descrita por estas partículas o cuerpos recorren el lugar geométrico de una hipérbola, esto se fundamenta esencialmente por el tipo de excentricidad de la órbita la cual es mayor a 1.

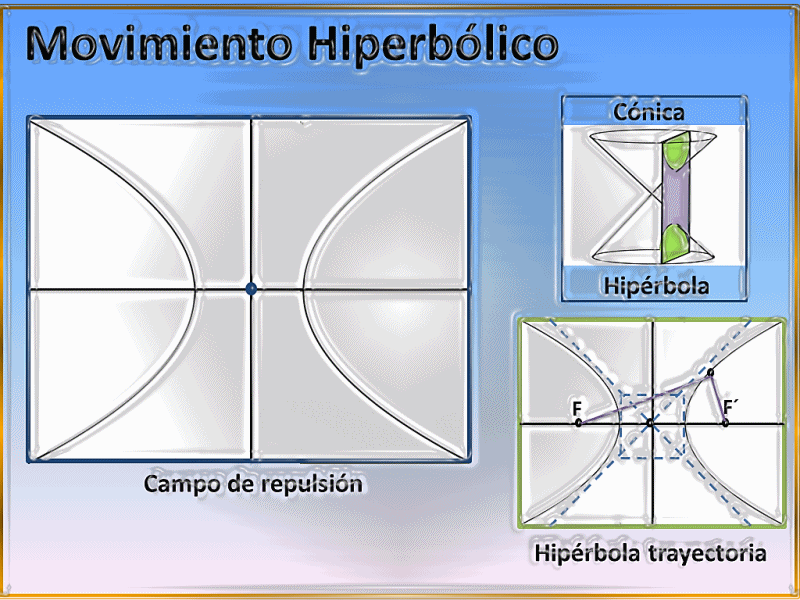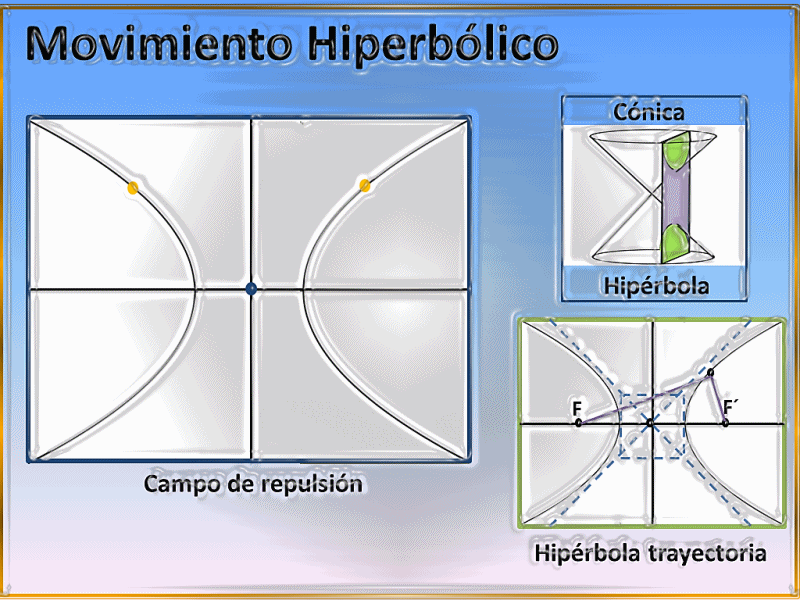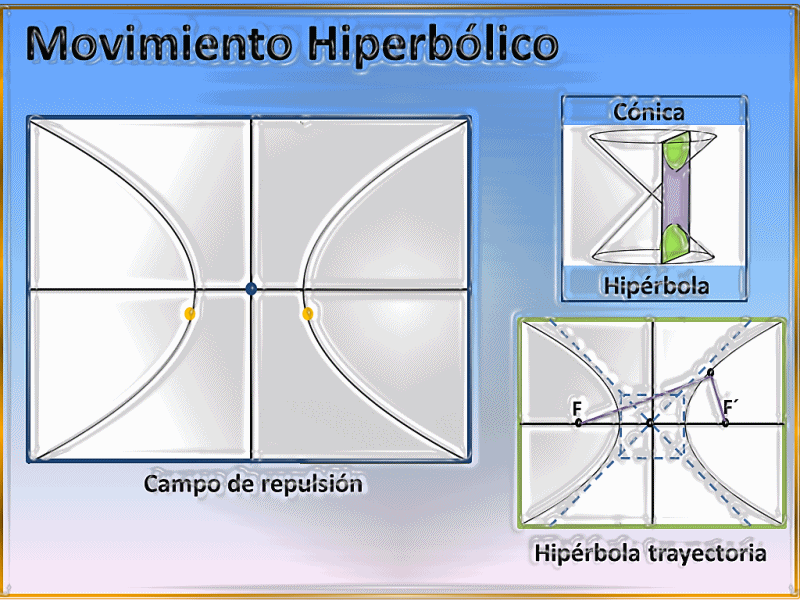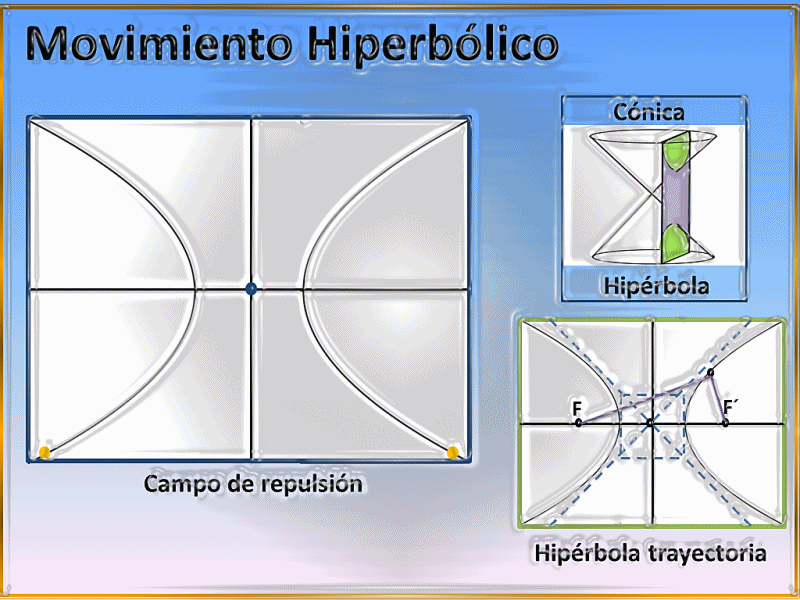
Debemos tener en cuenta que si estamos en presencia de un campo de repulsión la trayectoria seguida por cualquier partícula o cuerpo que se quiera aproximar al mismo siempre será la del lugar geométrico de una hipérbola, describiendo entonces el conocido e importante movimiento hiperbólico, un ejemplo histórico de este tipo de trayectoria lo ha representado la famosa dispersión de las partículas alfas por los núcleos atómicos, debido a que al disparar partículas de este tipo hacia el núcleo de un determinado átomo llegará un momento en donde algunas serán repelidas por dicho núcleo, siguiendo de esta forma trayectorias de tipo hiperbólicas, esta actividad la desarrolló experimentalmente el físico Ernest Rutherford.

Para este caso conoceremos algunos modelos matemáticos específicos utilizados durante el estudio de algún tipo de movimiento hiperbólico mediante el apoyo de la figura geométrica de la hipérbola.

Trayectoria hiperbólica

Es importante relacionar a la elipse y la hipérbola debido a que ambas guardan ciertas relaciones con respecto a sus elementos y de allí se hace útil la relación de estas dos curvas ya que el estudio del movimiento elíptico nos permite apoyarnos para el movimiento hiperbólico, por lo tanto podemos expresar nuevamente que la figura geométrica de la elipse al igual que la hipérbola son curvas con grandes simetrías en relación a un eje perpendicular al plano focal, cuyo centro es (O) con dos focos (FF´) y en donde cierto segmento o porción del eje focal lo llamamos también eje transverso (eje mayor) y cierto segmento del eje perpendicular lo denominamos eje conjugado (eje menor), los vértices de estas curvas son puntos de las mismas y anclados sobre los respectivos ejes antes mencionados, denominamos semieje transverso (a) la distancia media del eje transverso el cual se encuentra como expresamos sobre el eje focal, a las semidistancias focales la denominamos c, dándose la relación c = ae, a continuación mostraremos la siguiente figura 2 la cual representa una trayectoria hiperbólica con sus asíntotas permitiéndonos extraer relaciones o ecuaciones matemáticas importantes implementadas en el estudio del movimiento hiperbólico.

Figura 2. Trayectoria hiperbólica.

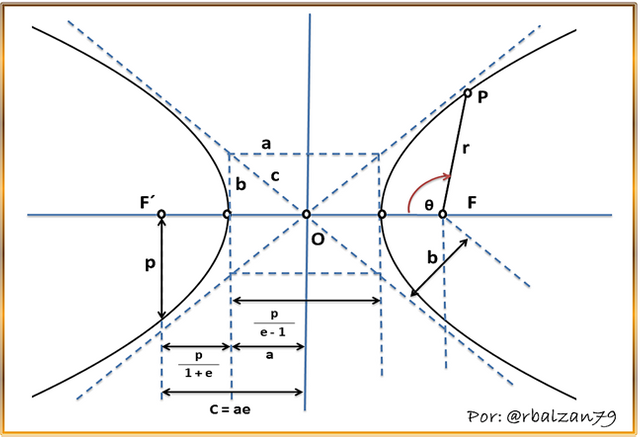
De acuerdo a la anterior imagen podemos considerar las siguientes ecuaciones geométricas necesarias para el análisis de los distintos movimientos hiperbólicos en nuestro universo.

Para poder determinar nuestra primera ecuación podemos realizar el siguiente análisis, el aspecto conceptual de la hipérbola nos indica que el valor de c > a, entonces la diferencia entre c2 – a2 dará siempre un valor positivo y esto hace que le asignemos analíticamente a dicho valor (b2) o utilizando la trigonometría (según figura 2) para relacionar a tales literales, de esta manera la relación entre a, b y c será a través la siguiente expresión:

Unas de las más importantes características de la hipérbola y por lo tanto del movimiento hiperbólico lo representa su excentricidad simbolizada por la literal (e) y la cual está conformada por la siguiente ecuación:

Seguimos con la determinación de otras ecuaciones matemáticas extraídas de la figura 2 en relación al semieje transverso (a) y semieje conjugado (b):

De esta manera continuamos con la determinación de formulaciones matemáticas, en esta oportunidad las ecuaciones que describen el lugar geométrico de la hipérbola, por lo tanto tomaremos en cuenta que dicha hipérbola tendrá como centro (C) el origen (O) de un plano cartesiano coordenado y cuyo eje focal coincide con el eje de las X, para este caso tenemos la siguiente expresión:

Para el caso en donde la trayectoria de la hipérbola tenga como centro el origen de un plano coordenado y ahora su eje focal coincide con el eje de las Y, tenemos la siguiente expresión:

Las fórmulas antes planteadas representan modelos matemáticos que sirven de base fundamental para el estudio de manera general de cualquier partícula, cuerpo u objeto que describa en su trayectoria o recorrido una hipérbola, e implementadas por la cinemática para el análisis de los distintos tipos de movimientos hiperbólicos.

La Hipérbola en la cinemática de algunas partículas, cuerpos u objetos que orbitan en nuestro universo

Desde el punto de vista de nuestra astronomía o más específicamente de la mecánica celeste, en donde la cinemática ha jugado un extraordinario papel gracias a los aportes de las maravillosas figuras cónicas entre las cuales encontramos a la hipérbola con todas esas expresiones o modelos matemáticos disponibles para la comprensión del fenómeno del movimiento hiperbólico.

Nuestro sistema solar a través de la acción gravitatoria del Sol representa un claro ejemplo de campo de fuerza central, esto hace que la energía potencial de una determinada partícula, cuerpo u objeto dependa sólo de su distancia a un punto fijo al cual se le denomina centro de dicho campo, esto permite que ciertos cuerpos materiales puedan atraerse con una fuerza la cual se encuentra dirigida en relación a la línea que los une y su intensidad será directamente proporcional al producto de las masas de dichos cuerpos pero inversamente proporcional al cuadrado de la distancia que los separa, formando entre ambos cuerpos órbitas circulares o elípticas como lo pudimos observar en la pasada publicación sobre movimiento elíptico.

Es importante recordar siempre que las diferentes órbitas que se desarrollan en nuestro universo dependerán del grado de la excentricidad (e) de su trayectoria o recorrido, por lo tanto, para las órbitas circulares (e = 0), elípticas (0< e <1), parabólicas (e = 1) e hiperbólicas (e > 1). La excentricidad de la hipérbola le ofrece una órbita a cualquier cuerpo u objeto que le permite escapar de la acción gravitatoria de un determinado cuerpo de fuerza central.

Resaltando enormemente la característica de excentricidad de tal órbita debido a que su valor será mayor a 1, esto nos permite recordar la ecuación para la velocidad de escape necesaria para que un cuerpo salga de la atracción del campo gravitatorio de la tierra, debido que al conocer este valor podríamos determinar el recorrido o trayectoria de cualquier tipo de órbita de una partícula cuerpo u objeto esto desde el punto de vista astronómico, por lo tanto tenemos la siguiente fórmula para el valor de la velocidad de escape:

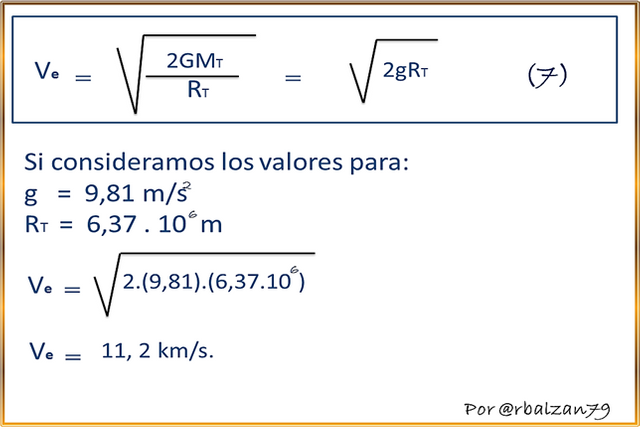
Una vez conocida el valor de dicha velocidad inicial de escape podemos mencionar que este tipo de desplazamiento lo conocemos también como trayectorias de escape según sea el caso de estudio, como por ejemplo en el lanzamiento de los satélites artificiales los cuales podrán describir distintas trayectorias como la de un círculo, parábola, elipse e hipérbola, todo dependerá de la velocidad con la cual sean lanzados, por lo tanto si dicha velocidad está por debajo a la de escape, el satélite describirá una órbita circular o elíptica si la velocidad es igual a la de escape la trayectoria de la órbita será de tipo parabólica y si dicha velocidad es mayor a la de escape la trayectoria que recorrerá la órbita será la de una hipérbola generándose un movimiento hiperbólico.

En el último caso que es el central para esta publicación podríamos expresar de forma simplificada que debido al exceso de velocidad final en comparación con un determinado cuerpo central dicha partícula, cuerpo u objeto viajará o se dirigirá al infinito, recalcando que la energía total de este tipo de órbita hiperbólica es positiva y llegando al infinito sin agotar su energía cinética.

La cinemática en la trayectoria o recorrido de una órbita hiperbólica

Esta ciencia del movimiento se ha nutrido constantemente de formulaciones matemáticas para poder dar respuesta a las innumerables inquietudes sobre los distintos tipos de movimiento que ocurren en nuestro complejo universo, y el fenómeno relacionado al desplazamiento de cualquier partícula, cuerpo u objeto mediante un recorrido o trayectoria hiperbólica representa el menos común entre los tipos de movimientos presente entre nosotros, sin embargo, esto no quiere decir que lo convierta en el menos importante debido a que muchos actividades del campo de la ciencia guardan algún tipo de relación con este tipo de fenómenos hiperbólico, en especial la astronomía y la física como hemos comprobado en el presente artículo.

Una de las características más resaltante de la cinemática está relacionada con las ecuaciones de la velocidad en este caso orbital, ya que para cualquier partícula, cuerpo u objeto es necesario determinar adecuadamente su velocidad orbital, podríamos decir que tiene que ser concreta ya que la misma le permitirá orbital una trayectoria especifica como lo hemos visto desde el inicio con el análisis del movimiento circular, parabólico, elíptico y ahora hiperbólico, claro también dependerá del tipo de lugar o espacio en que se encuentre dicho cuerpo u objeto de estudio ya que esto determinará el tipo de campo de fuerza que ejercerá una determinada acción sobre tal cuerpo.

Velocidad orbital (v)

Cuando un determinado cuerpo u objeto describe en su recorrido una trayectoria hiperbólica podemos utilizar la siguiente ecuación:

Tomando en cuenta ciertos cálculos estándar para dicha velocidad orbital (v) en cualquier lugar de la órbita se verifica la siguiente relación:

Con esto podemos expresar que al adicional un diferencial de velocidad relativamente pequeño el cual es requerido para acelerar hasta alcanzar la velocidad de escape, esto en el infinito representará una velocidad relativamente grande.

De esta forma pudimos conocer algunas expresiones o ecuaciones matemáticas específicas utilizadas para el análisis del movimiento hiperbólico en particular en la cinemática de las distintas partículas, cuerpos u objetos que orbitan en nuestro universo y que gracias a la geometría analítica a través de las figuras cónicas en especial la hipérbola han contribuidos en la determinación de distintas órbitas esenciales para el estudio de la mecánica celeste.

1.- Continuamos comprobando que esta rama de las matemáticas nos ha dado cualquier tipo de herramientas para poder realizar infinidades de estudios relacionados con distintas áreas del campo de la ciencia en general, como lo hemos observado en su nexo con la física a través de la cinemática, por lo tanto nuestro entorno será mejor comprendido y analizado con la ayuda de la fabulosa ciencia de las formas y las figuras, es decir, geometría analítica.

2.- Los modelos matemáticos siempre representaran para la física la base fundamental para su continuo y permanente crecimiento, en el análisis de cada uno de los de los movimientos según el recorrido de su trayectoria partimos con el movimiento circular, luego el parabólico, después el elíptico y ahora el hiperbólico en este espectacular recorrido nos hemos nutrido de este maravilloso nexo y comprendido que la cinemática y la geometría estarán unidas por siempre y lo más importante en pro de todos nosotros.

3.- La figura cónica de la hipérbola guarda mucha simetría con la elipse, a pesar que la primera representa una curva abierta formada por dos tramos y cuyo valor absoluto de la diferencia de sus distancias a los focos o puntos fijos es constante y por lo antes descrito el valor de esta constante es positivo y menor que la distancia focal, en cuanto a la elipse constituye una curva cerrada e igualmente con dos focos o puntos fijos y cuya suma de sus distancias desde un punto cualesquiera de dicha curva a tales puntos fijos será también una constante pero para este caso el valor de tal constante es mayor a la distancia focal, muchos elementos de una nos ayudan a comprender a la otra curva esta característica es lo que permite que ambas sean de gran utilidad en el mundo científico, debido a que muchas formulaciones matemáticas son aplicables en una trayectoria tanto elíptica como hiperbólica como notamos en los movimientos de cualquier partícula , cuerpo u objeto se transite sus respectivos lugares geométricos.

4.- Este artículo nos permitió comprender y analizar algunas características de manera general de las órbitas hiperbólicas y su relación geométrica con la figura de la hipérbola a través de sus elementos como la excentricidad por nombre tal solo uno pero de mucha relevancia en el estudio del movimiento hiperbólico desarrollado por la cinemática mediante sus aplicaciones con características de movimiento con magnitudes importantes como la velocidad, todo esto bajo la ayuda de la astronomía y su mecánica celeste, en donde sabemos tanto la geometría y cinemática han brindados sus esenciales frutos.

5.- Para concluir mis amigos y apreciados lectores, La geometría analítica con la cinemática representan un claro ejemplo de enseñanza para todos ya que a pesar que son muy complejas pero son realmente grandiosas, de nuevo resultó un grato placer hacer coincidir a estas dos formidables ciencias, es decir, las Matemáticas y la Física, y como en los anteriores artículos expresamos que sin ellas nada lograríamos y de ellas hemos aprendido a ser una especie ampliamente intelectual y de esta manera con gigantescos desarrollos sociales.

Hasta otra oportunidad mis apreciados lectores de steemit, en especial a los miembros de la gran comunidad de #STEM-Espanol, los cuales reciben el apoyo de otras dos grandes comunidades como los son #steemstem, #utopian-io y #curie, por lo cual recomiendo ampliamente formar parte de este hermoso proyecto, ya que resalta la valiosa labor de la academia y del campo científico, pero sobre todo, por el gran respecto, dedicación y ayuda para sus miembros.

Nota: Todas las imágenes fueron elaboradas usando las aplicaciones Paint, Power Point y el gif con la aplicación de PhotoScape.

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.

[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.

[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.

[4] Gómez Ana Inés. Órbitas en el sistema solar, Volumen 3. Facultar de ciencias matemáticas, Universidad Complutense de Madrid.

[5] De Bernardini Enzo. Leyes de Kepler. Astronomía Sur. Http://astrosurf.com/astronosur, UNLP, 1998.

[6] Alegría Pedro. Las cónicas y sus aplicaciones.pedro.alegrí[email protected].

[7] O. Montebruck, E. Gill. Órbitas de satélite.

[8] Williams J. Astore, Robert B. Giffen, Wiley J. Larson, Comprensión del
Espacio, segunda edición, 2004.

[9] Raymond Chang, Williams College. Séptima Edición. Editorial McGrawHill. México, 2002.