Physics - Classical Mechanics - Rigid Body Equilibrium
[Image 1]
Introduction
Hey it's a me again @drifter1! Today we continue with Physics and more specifically the branch "Classical Mechanics" to get into a new "chapter" called Equilibrium and Elasticity. In this chapter we will get into more advanced equilibrium problems that include both translational and angular motion. To get more specific this article is basically an introduction to rigid bodies and how we define equilibrium for them. So, without further ado, let's dive straight into it!
Equilibrium Conditions of Rigid Bodies
Up to this point in the series we mainly talked about point equilibrium, describing rigid bodies as a single point called the center of mass. After the introduction of angular motion and torque we can redefine equilibrium as a state where a rigid object doesn't move and/or rotate. This is actually the definition of static equilibrium. Another form of equilibrium is dynamic equilibrium, where an object is moving (or rotating) at constant velocity.Two conditions have to be met for a rigid body to be in equilibrium:
- The net force in all directions must be zero
- The net torque acting on the object must be zero
Mathematically, we can define those conditions as:
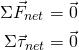
Net Force Condition
Getting more in-depth, in order to achieve the first condition the forces acting along all axes of motion must sum to zero. Thus, In two-dimensional space (x and y axes) we can write: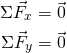
A great formula that can be used here is Newton's second law that connects force and acceleration:
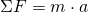
Net Torque Condition
To achieve the second condition, we first have to recall the quantities torque depends on. Thinking about the definition of torque for simple linear bodies, which is τ = Fl, we understand that torque depends on the force and lever arm.When the second condition is met, the body is spinning with constant angular velocity (or not rotating at all), having zero angular acceleration. An easy way to check for this condition is the reformulation of Newton's second law for angular motion, which is:
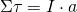
Of course torque can be written in respect to the various motion axes.
Center of Gravity
First of all, don't confuse center of gravity with center of mass! They are the same point only when inside of uniform gravitational fields. The center of mass is an imaginary point in space where the distributed mass sums to zero. The center of gravity, on the other hand, is a point through which the weight of the rigid body acts and where applying a force directly opposing the force of gravity balances the object.Let's proof why the COM and COG are the same in uniform gravitational fields...
COM = COG proof
Let's suppose a number of point masses m1, m2, etc. inside of three-dimensional space, located at the points (x1, y1, z1), (x2, y2, z2) etc. The coordinates of the center of mass (xcm, ycm and zcm are given by: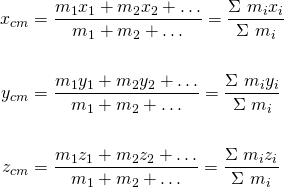
We can also write down the position in form of a position vector rcm:
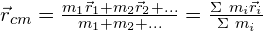
The torque of gravity for any of these points can be defined as:
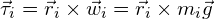
The total torque is therefore:
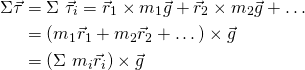
Multiplying and dividing by the total mass M, and substituting various equations that have been found previously during the calculation, we end up with:
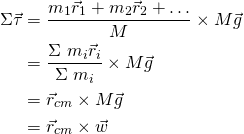
So the total torque is equal to the torque of gravity that acts on the center-of-mass (rcm). This basically tells us the the center-of-gravity is equal to the point of center-of-mass. During the calculation we supposed that g is the same for all the point masses. If it weren't then the center-of-gravity would of course end up being at a different position. This is something that occurs on planets, moons and bodies in general that have non-uniform mass distribution that also means non-uniform gravity.
Solving Equilibrium Problems
To solve problems around Rigid Body Equilibrium we use free-body diagrams that describe an idealized model of the system. Such a diagram shows all the external forces (actions and reactions).The steps for creating a free-body diagram can be summarized as:
- Draw the outlined shape of the body.
- Show all external forces (active loads, weight of the body, support reactions)
- Label all forces with their magnitudes and directions (indicate dimension using subscripts like Fx, Fy etc.).
You can find examples/exercises around such problems in Reference [5]
RESOURCES:
References
- https://courses.lumenlearning.com/boundless-physics/chapter/conditions-for-equilibrium/
- https://www.mun.ca/physics/undergraduates/fylabs/p1020/experiment6.pdf
- https://www.britannica.com/science/centre-of-gravity
- https://www.kpu.ca/sites/default/files/Faculty%20of%20Science%20%26%20Horticulture/Physics/Ch5-%201%20-%20Static%20Equilibrium_0.pdf
- https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_I_-_Mechanics%2C_Sound%2C_Oscillations%2C_and_Waves_(OpenStax)/12%3A_Static_Equilibrium_and_Elasticity/12.2%3A_Examples_of_Static_Equilibrium
Images
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
- Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
- Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
- Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
- Internal Energy and Work -> Internal Energy, Internal Work
Momentum and Impulse
- Conservation of Momentum -> Momentum, Conservation of Momentum
- Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
- Collision Examples -> Various Elastic and Inelastic Collision Examples
- Impulse -> Impulse with Example
- Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
- Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis
Angular Motion
- Angular motion basics -> Angular position, velocity and acceleration
- Rotation with constant angular acceleration -> Constant angular acceleration, Example
- Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
- Parallel Axis Theorem -> Parallel axis theorem with example
- Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
- Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
- Work and Power in Angular Motion -> Work, Work-Energy Theorem, Power
- Angular Momentum -> Angular Momentum and its conservation
- Explaining the Physics behind Mechanical Gyroscopes -> What they are, History, How they work (Precession, Mathematical Analysis) Difference to Accelerometers
- Exercises around Angular motion -> Angular motion examples
Final words | Next up
And this is actually it for today's post!Next time we will continue with Force Couples...
See ya!
Keep on drifting!


Congratulations @drifter1! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPThis post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Hi @drifter1!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 3.512 which ranks you at #6802 across all Steem accounts.
Your rank has dropped 6 places in the last three days (old rank 6796).
In our last Algorithmic Curation Round, consisting of 177 contributions, your post is ranked at #160.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server