Physics - Classical Mechanics - Exercises around Angular motion

[Image 1]

Introduction

    Hey it's a me again @drifter1! Today we continue with Physics and more specifically the branch "Classical Mechanics" to get into Exercises around Angular motion. I suggest you to read the previous articles of this chapter before this article. As always I will split the Examples into sections that correspond to the various articles of this chapter. So, without further ado, let's dive straight into it!

---

Basics

    Let's consider an object is moving along a circle with radius r = 0.5 m, needing T= 5 sec to do a complete cycle.

Calculate the following:

1. the angular velocity ω if it's angular acceleration is zero
2. the angular position θ after 8 seconds

1. Angular velocity

The circumference of a circle is given by 2πr.

    Knowing that the object's period is 5 seconds and that it travels a distance of 2πr doing that cycle, we can easily calculate the average velocity of the object as:

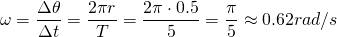
2. Angular position

    Using the same equation we can also calculate the position of the object after 8 seconds by simply substituting the calculated angular velocity ω and time, as following: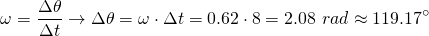

---

Constant Angular Acceleration

    Let's now suppose an object that is moving in a circle of radius r = 5m with a constant angular acceleration of unknown value, starting at rest from θ = 0° and reaching an angular velocity ω = 30 rad/s after t = 15 sec.

Calculate the following:

1. The angular acceleration of the object
2. The angular position and velocity after t = 25 sec (from rest)

1. Angular acceleration

    Angular velocity is given by the following equation that contains the initial and final angular velocity value, time and angular acceleration: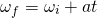


    Knowing the time that has passed (t = 15 sec), the initial value (0 rad/s - at rest) and final value (30 rad/s - given) of angular velocity, we can easily find the angular acceleration:

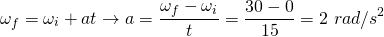
2. Angular position and velocity

    Using the same equation we can easily find the angular velocity after t = 25 seconds: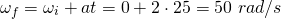


    Knowing that we start from θ = 0° degrees, we just have to substitute all our known quantities into the equation of angular position:

---

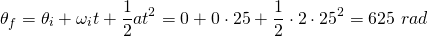
Rotational Kinetic Energy - Moment of Inertia

    Suppose that we have a linear rod of length L = 0.4m and mass M = 1Kg. It has been proven that the Moment of Inertia about the center is given by: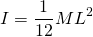


Considering a constant angular velocity of ω = 1 rad/s, calculate :

1. The kinetic energy if the rod rotates about the center
2. The kinetic energy if the rod rotates about a point parallel to the center with a distance of d = 0.1m

1. Rotate about the center

    To calculate the kinetic energy we just have to substitute the values into the equation of kinetic energy, as the moment of inertia about the center is already known: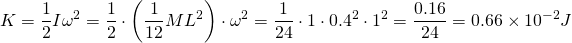

2. Rotate about a point parallel to the center

    When rotating about an axis parallel to an axis for which we know the moment of inertia, we have to use the Parallel Axis or Huygens-Steiner Theorem to find the moment of inertia along the parallel axis. That way we have: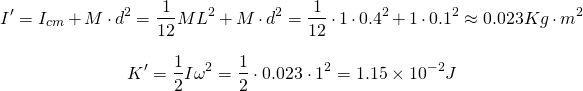

---

Torque and Angular Acceleration

    Let's consider a constant force F = 10N acts at an angle of θ = 45° on the second point (parallel to the center at a distance of d = 0.1m) of the previous example's object

Calculate:

1. The torque from that force
2. The angular acceleration of the object

1. Torque

Using the definition of torque we have: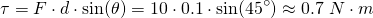

2. Angular acceleration

    The total torque is equal to the product of I and a, and thus using that we can calculate the angular acceleration, because the other quantities are known: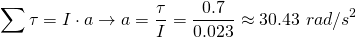

---

Rolling motion

    Consider the same object as in the example about rotational kinetic energy. Let's suppose that this object also moves in Translational motion, meaning that it's axis of rotation is moving with some speed through space and time. Combining these two motions, we basically end up with Rolling motion. So, knowing that the speed of it's center of mass is v = 0.5 m/s and talking about the first case of rotating about the center, calculate the total kinetic energy of the object.

Solution

    The total kinetic energy is equal to the sum of rotational and translational kinetic energy. We already know the first term and so by simply calculating the translational kinetic energy, we can calculate the total energy as: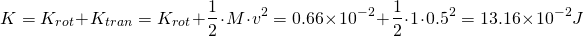

---

Work and Power

    Let's calculate the work and power of the torque that we had in the example about torque, supposing a distance of 2π and that the rod starts at rest.

The angular velocity after travelling a distance of 2π is:

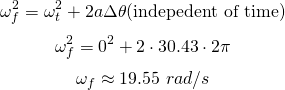
Work

    From the Work-Energy Theorem, we know that the Work is equal to the change in kinetic energy. Because the initial kinetic energy is zero, we can easily calculate the work: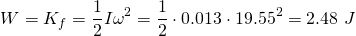

Power

We already calculated the final angular velocity and thus the power: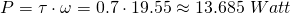

---

Angular Momentum

    Let's lastly also calculate the angular momentum at the same moment as in the previous example (word play), as we already know all terms: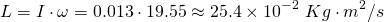

---

RESOURCES:

References

My previous articles...

Images

1. https://commons.wikimedia.org/wiki/File:Classical_angular_momentum.svg

Mathematical equations used in this article, where made using quicklatex.

---

Previous articles of the series

Rectlinear motion

• Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
• Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
• Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
• Rectlinear motion exercises -> examples and tasks in rectlinear motion

Plane motion

• Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
• Projectile motion as a plane motion -> missile/bullet motion as a plane motion
• Smooth Circular motion -> smooth circular motion theory
• Plane motion exercises -> examples and tasks in plane motions

Newton's laws and Applications

• Force and Newton's first law -> force, 1st law
• Mass and Newton's second law -> mass, 2nd law
• Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
• Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
• Contact forces and friction -> contact force, friction
• Dynamics of Circular motion -> circular motion dynamics, applications
• Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
• Contact force and friction examples -> exercises in force and friction
• Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
• Advanced Newton law examples -> advanced (more difficult) exercises

Work and Energy

• Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
• Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
• Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
• Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
• Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
• Internal Energy and Work -> Internal Energy, Internal Work

Momentum and Impulse

• Conservation of Momentum -> Momentum, Conservation of Momentum
• Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
• Collision Examples -> Various Elastic and Inelastic Collision Examples
• Impulse -> Impulse with Example
• Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
• Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis

Angular Motion

• Angular motion basics -> Angular position, velocity and acceleration
• Rotation with constant angular acceleration -> Constant angular acceleration, Example
• Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
• Parallel Axis Theorem -> Parallel axis theorem with example
• Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
• Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
• Work and Power in Angular Motion -> Work, Work-Energy Theorem, Power
• Angular Momentum -> Angular Momentum and its conservation
• Explaining the Physics behind Mechanical Gyroscopes -> What they are, History, How they work (Precession, Mathematical Analysis) Difference to Accelerometers

---

Final words | Next up

And this is actually it for today's post!

Next time we will start a new Mechanics "chapter"...

See ya!

Keep on drifting!