DIFERENCIAL DE UNA FUNCIÓN EN UN PUNTO

imagen copiada de Pixabay
Por fin ya puedo compartir otra publicación con ustedes, y he elegido como tema aplicar el concepto de diferencial de una función en un punto, en la resolución de problemas relativos a la geometría, física y electricidad para los que se requiere una aproximación de una determinada variable, error absoluto, relativo y porcentual.
DIFERENCIAL DE UNA FUNCIÓN EN UN PUNTO
Sea 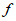 una función real de una variable real. Si
una función real de una variable real. Si 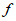 es derivable en el punto “
es derivable en el punto “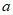 ”, existe entonces el límite,
”, existe entonces el límite,
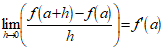 (1)
(1)Ahora bien, la expresión (1) puede escribirse equivalentemente de la forma,
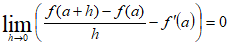 (2)
(2)o también,
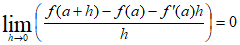 (3)
(3)Nótese que para que el límite (3) sea igual a cero, el numerador debe tender a cero mucho más rápidamente que el denominador, y esto nos dice que para valores “muy pequeños” de “ 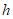 ”, la cantidad
”, la cantidad 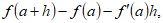 debe ser aproximadamente igual a cero. Expresaremos esto último escribiendo,
debe ser aproximadamente igual a cero. Expresaremos esto último escribiendo,
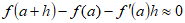 (4)
(4)o lo que es lo mismo,
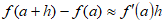 (5)
(5)Para un valor fijo de “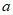 ” en el dominio de la función, la cantidad , es una función de la variable “
” en el dominio de la función, la cantidad , es una función de la variable “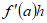 ” y esto nos conduce a la siguiente definición:
” y esto nos conduce a la siguiente definición:
DEFINICIÓN: Si 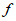 es una función derivable en un punto “
es una función derivable en un punto “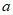 ” de su dominio, se define el diferencial de
” de su dominio, se define el diferencial de 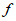 en “a”, que denotamos por
en “a”, que denotamos por 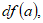 como la función,
como la función,
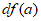 :
: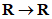
definida por,
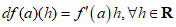 (6)
(6)Para una función derivable en todo punto de su dominio, podemos escribir:
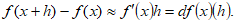 (7)
(7)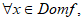 y valores “muy pequeños de “h”.
y valores “muy pequeños de “h”.
En la literatura clásica, en lugar de “h” se empleaba 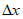 , para referirse a un pequeño incremento dado a la variable independiente “x” y la (7) aparece como:
, para referirse a un pequeño incremento dado a la variable independiente “x” y la (7) aparece como:
 (8)
(8)El primer miembro, es decir, el incremento que se ocasiona en la variable dependiente 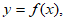 al pasar de “x” a “x+
al pasar de “x” a “x+ x ”, era denotado por
x ”, era denotado por  y en la literatura clásica y por ello la (8), también es presentada como:
y en la literatura clásica y por ello la (8), también es presentada como:
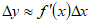 (9)
(9)Más formalmente, si en la (7) usamos la notación,
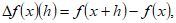
entonces podemos rescribirla como:
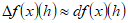 (10)
(10)para f derivable en “x” y “h” “muy pequeño”.
La notación en (10) es muy recargada y so pena de perder rigor, pero teniendo claro el contexto, abreviamos la escritura poniendo:

(donde:
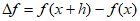 y
y 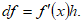 ).
).
Para la función identidad sobre los reales, esto es, la función: 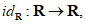 tal que,
tal que, 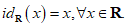
queda claro que su diferencial en cualquier punto, es la propia función identidad (por ser su derivada la función constante igual a 1), es decir, para 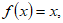
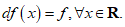
ya que para cualquier 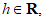 se verifica que:
se verifica que:
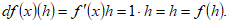
Usando pues ese resultado, de que para la función identidad (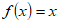 ), resulta
), resulta 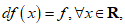 , denotaremos también por “d_x_” la función identidad sobre los reales. En ese contexto, para cualquier función f derivable en un punto “x” de su dominio, podemos escribir:
, denotaremos también por “d_x_” la función identidad sobre los reales. En ese contexto, para cualquier función f derivable en un punto “x” de su dominio, podemos escribir:

de modo que,
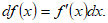 (11)
(11)o en el lenguaje de los clásicos:
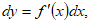 (12)
(12)para una función 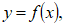 y que por otra parte, pretende justificar la notación de Leibnitz al escribir:
y que por otra parte, pretende justificar la notación de Leibnitz al escribir:
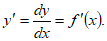
Muy a menudo deseamos calcular o estimar dentro de márgenes seguros, el cambio en el valor de una función causado por un pequeño cambio en el valor de la variable independiente. Como se observó anteriormente, cuando “h” es “pequeño”, 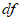 y
y  son en general, cercanamente iguales y en muchos casos el valor de
son en general, cercanamente iguales y en muchos casos el valor de 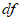 provee una aproximación suficientemente buena al valor de
provee una aproximación suficientemente buena al valor de 
En cualquier cómputo aproximado, la cantidad en que difieren el valor computado de la función, del verdadero valor, se llama el error del cómputo. Así pues, si calculo 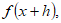 cuando lo que verdaderamente deseo calcular es
cuando lo que verdaderamente deseo calcular es 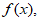 entonces, el error cometido en el cómputo es:
entonces, el error cometido en el cómputo es:
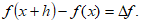
Al valor absoluto,
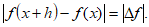
lo llamaremos el error absoluto, y, al cociente,
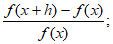
lo llamaremos, el error relativo.
Al porcentaje,
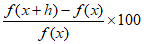 %
%lo referimos como el error porcentual.
Espero que no la interpretación de este contenido no se haga tediosa, de todas formas acepto consejos y sugerencias para mejorar, he tardado en publicar porque no encontraba la forma de colocar las ecuaciones y expresiones matemáticas, gracias a Dios ya encontré una forma muy fácil de hacerlo. Elegí este tema como una prueba piloto ya que he leído que existe una comunidad llamada @steemstem y @stem-espanol conformadas por profesionales de alto nivel, así que no quise irme por lo básico, pero como dije, acepto sugerencias, si quieren bajar de nivel con gusto lo haré, si quieren seguir por lo avanzado entonces seguiremos con el tema de integrales en las próximas entregas. Espero que sea de tu gusto este artículo.
Lecturas que recomiendo
Juan Luis Corcobado Cartes y Javier Marijuán López. Matemáticas I C.O.U Opciones A y B.
Louis Leithold. El Cálculo 7ma Edidción.
Pepperdine University

muy buena tu publicación con el razonamiento matemático aplicado en "DIFERENCIAL DE UNA FUNCIÓN EN UN PUNTO" saludo y éxito @apvk
@apvk cuando vi tu introducción me emocioné y dije "voy a seguir de cerca su contenido para ponerme muy lista en matemáticas y aprender lo que me falta" , ahora leo tu segunda publicación y me siento igual de perdida que en mi clase de matemáticas I en la universidad.
Creo que definitivamente las matemáticas no son lo mío y por eso me terminé cambiando de carrera.
Sin embargo tu contenido es muy bueno, gracias por compartirlo.
¡Saludos!
Jajaja. Gracias por tu comentario, lamento que mi contenido no sea afín a tus intereses. Igual admiro el esfuerzo que haces al tratar de entender aunque sin éxito. Saludos!!
@apvk yo tengo el Leithold 7ma edición y para mí eso es chino, no entiendo casi nada.
También tengo el Purcell 9na edición, que era con el que solía estudiar y me costaba entender, entonces uno de mis profesores me decía "si no entiendes con el Purcell, pues, no sé que haré contigo, el Purcell es el Bamby de los libbros de cálculo" jajaj
¿Qué recomendación podrías darme para ver si puedo despertar mi avidez en el tema de las matemáticas?
apvk como hiciste para poder poner las ecuaciones en el mark down? por cierto muy buena explicación me hiciste recordar mis días en la universidad ya que fui estudiante de ingeniera en telecomunicaciones
Hola, las escribes en microsoft word en insertar ecuaciones, luego las copias y pegas en power point y sin modificar nada copias de power point y pegas en tu artículo, entonces se pega como una imagen!! gracias por comentar!
La verdad que ese repaso que has hecho de la derivada de una función está muy bien llevado.
Las imágenes de las ecuaciones o formulas son excelentes.
Pero todo lo supera la explicación.
Soy Ingeniero Civil y jubilado como profesor Universitario y percibo este trabajo con mucha intensidad.
Buen trabajo matemático.
Muy buen post. gracias por publicar.
Congratulations @apvk! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPYou got a 8.99% upvote from @upme thanks to @apvk! Send at least 3 SBD or 3 STEEM to get upvote for next round. Delegate STEEM POWER and start earning 100% daily payouts ( no commission ).
You got a 6.21% upvote from @postpromoter courtesy of @apvk!
Want to promote your posts too? Check out the Steem Bot Tracker website for more info. If you would like to support the development of @postpromoter and the bot tracker please vote for @yabapmatt for witness!
Sneaky Ninja Attack! You have just been defended with a 24.65% upvote!
I was summoned by @apvk. I have done their bidding and now I will vanish...
woosh
A portion of the proceeds from your bid was used in support of youarehope and tarc.
Abuse Policy
Rules
How to use Sneaky Ninja
How it works
Victim of grumpycat?
The force is with you! You got a 31.48% upvote from @steemyoda courtesy of @apvk!