En primer lugar mis saludos respetuosos para toda la comunidad académica y científica de steemit, en especial a #STEM-Espanol, #steemstem, #utopian-io, #cervantes y #entropia, con su valioso apoyo hacemos posible nuestro crecimiento en todos los aspectos en esta prestigiosa plataforma.

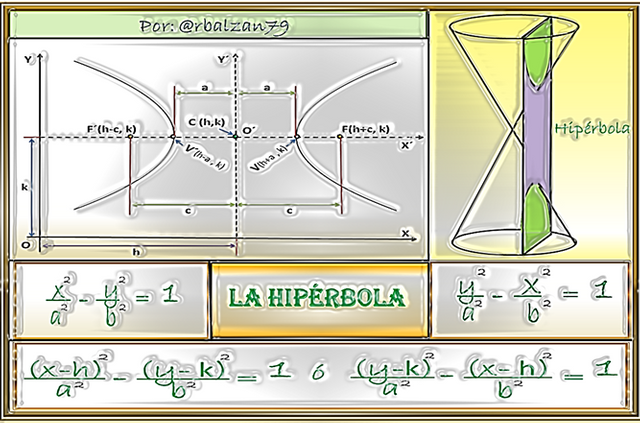
Seguimos con la temática geometría analítica plana, en donde, continuamos dando significativos pasos para la comprensión analítica de las matemáticas, en esta oportunidad estudiaremos a la hipérbola, por lo tanto, conoceremos la determinación de sus ecuaciones más fundamentales, con esto proseguimos con el análisis detallado de las ecuaciones y los lugares geométricos de una curva específica, determinando así, sus propiedades particulares, hasta ahora hemos estudiado a la línea recta, circunferencia, parábola y la elipse, recordando que en el análisis de la elipse realizamos un estudio más amplio ya que pudimos conocer su importancia en la determinación de grandes leyes que transformaron todo el campo de la ciencia y con ello todo lo referente a la sabiduría de la humanidad, en el presente artículo el propósito es el mismo, enfocar nuestro análisis tanto en la determinación de las ecuaciones de la curva llamada hipérbola e incentivar a la profundización en cuanto a su utilidad en nuestra vida cotidiana, para lograr un entendimiento más allá del ámbito académico.

Para definir esta importante curva, podemos expresar que es un lugar geométrico formado por el movimiento de un determinado punto en el plano, donde, el valor absoluto de la diferencia o resta de las distancias a dos puntos fijos (focos) será siempre igual a una cantidad fija o constante, positiva y menor que la distancias entre dichos focos.

A continuación mostraremos la siguiente imagen para poder analizar mejor y comprender la definición de esta importante curva, la hipérbola, con mayor facilidad, por lo tanto, tenemos:

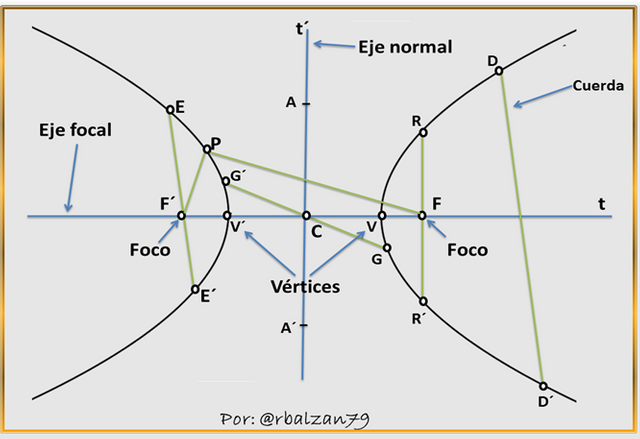
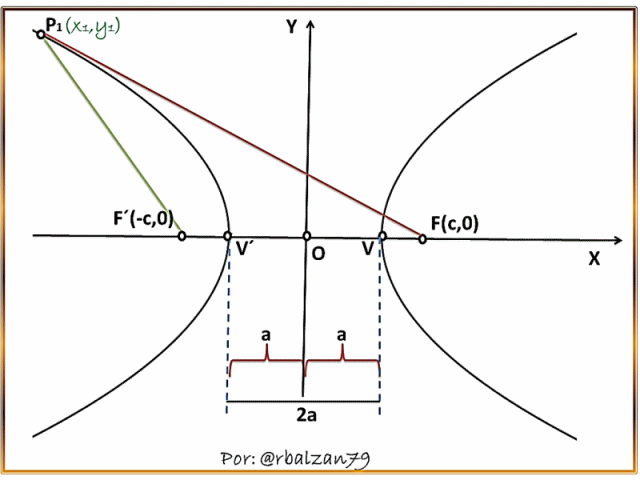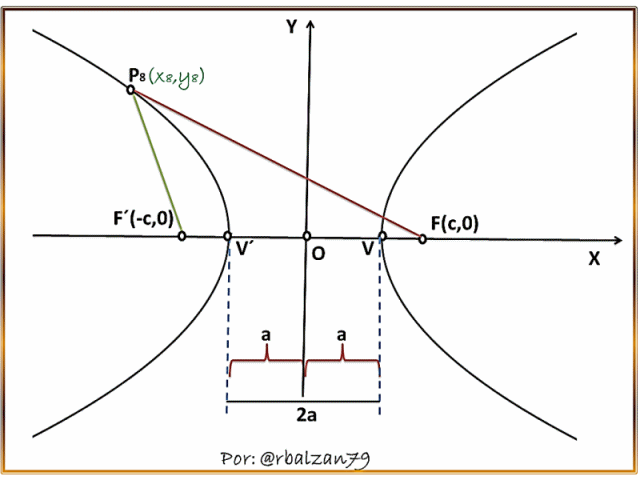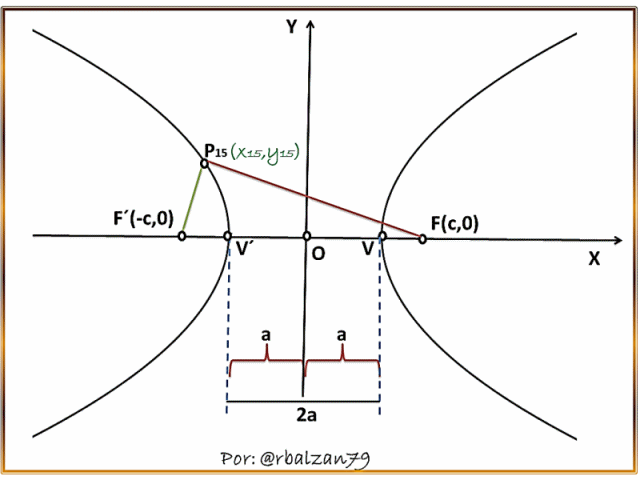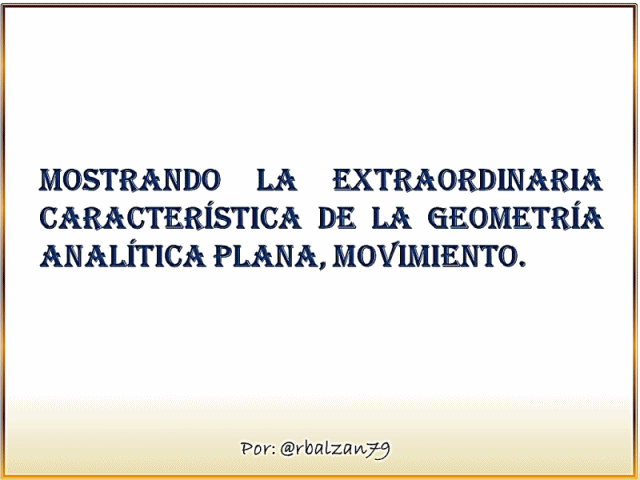
Para la determinación de esta ecuación tomaremos en cuenta la condición, en donde, la hipérbola tiene como centro el origen del plano y su eje focal coincide con el eje X, por lo tanto, los puntos fijos a los que hemos denominado focos se encuentran sobre dicho eje, el centro como expresamos estará representado por el origen (O), el cual será el punto medio del segmento originado entre los focos FF´, entonces, estos puntos tendrán como coordenadas F(c , 0) y F´(-c , 0), resaltando que c será una constante positiva, nos apoyaremos en la siguiente figura para realizar nuestro análisis.

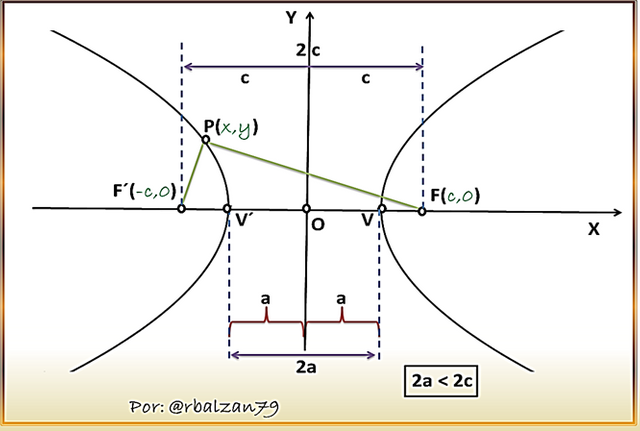
Si tenemos un punto P(x ,y) cualesquiera de dicha hipérbola, podemos expresar según la definición de hipérbola antes descrita, que el mencionado punto deberá satisfacer la siguiente condición geométrica:

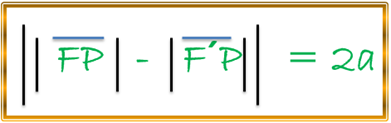
En la anterior expresión observamos la diferencia o resta en valor absoluto de las distancias que tenemos del punto P a cada uno de nuestros focos de la hipérbola, y que por definición sabemos que dicha diferencia siempre será constante, este resultado constante la representamos como 2a.

Debido a que dicho punto (P) se mueve como dijimos a lo largo del lugar geométrico que conforma la hipérbola, por lo tanto, mediante el movimiento de este punto encontraremos que va a concordar con el eje de las X para estas condiciones, y a su vez con cada uno de los vértices de dicha hipérbola, ya que los mismos están sobre tal eje, generando de esta forma los segmentos FV y F´V´ , los cuales sustituirán a FP y F´P respectivamente, y de esta manera logramos visualizar de mejor forma lo antes descrito , es decir, la condición geométrica antes planteada, como podemos observar en el siguiente gif animado, en donde, reflejamos el movimiento del punto (P) el cual describe una parte del lugar geométrico de la curva estudiada, resaltando de esta manera el carácter de movilidad brindado por esta parte de las matemáticas como lo es, la geometría analítica plana:

Luego de mostrar la extraordinaria capacidad que nos ofrece la geometría analítica con su inyección de movimiento a nuestros análisis, seguimos con el planteamiento ya descrito, por lo tanto, tenemos que (a) será una constante positiva y además 2a < 2c, por lo que la anterior condición es semejante a las siguientes dos relaciones:

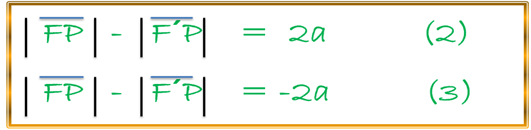
En donde, la relación que muestra 2a será cierta cuando el punto P se encuentre sobre la lado izquierdo de dicha hipérbola, mientras que la relación que muestra a -2a se comprueba cuando el punto P lo tengamos sobre el lado derecho de la mencionada curva.

Recordemos nuevamente la fórmula de la distancia para poder comprobar las anteriores relaciones o igualdades:

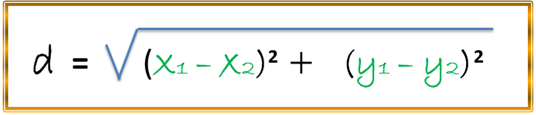
Esta fórmula la utilizamos para determinar la distancia entre los segmentos FP y F´P:

Seguimos con la determinación de la ecuación de la hipérbola de acuerdo a las condiciones geométricas descritas, comenzamos a resolver cualquiera de las dos relaciones mencionadas, es decir, (4) o (5), tomaremos la relación (4), para ello es conveniente realizar una serie de procedimientos algebraicos, entre los que se incluye el intercambio de miembros a ambos lados de la igualdad, luego elevar al cuadrado toda la expresión para después poder simplificar términos iguales como se muestra a continuación:

Con la finalidad de seguir simplificando la última expresión, elevamos nuevamente al cuadrado ambos miembros de la igualdad y desarrollamos los procedimientos correspondientes:

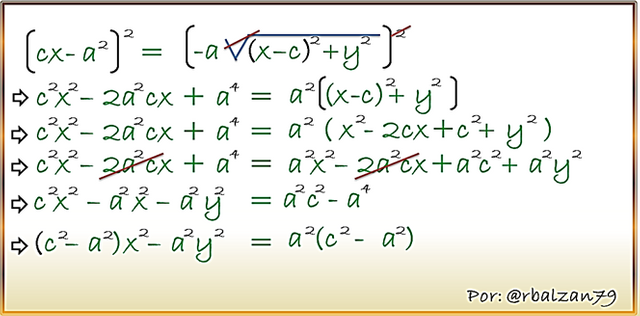
Antes de seguir, podemos realizar el siguiente análisis, como hemos notado según el aspecto conceptual de la hipérbola la cual nos indica que el valor de c > a, por lo tanto, la diferencia o resta entre c2 – a2 será siempre positivo y por lo cual podemos asignarle la literal b2, pero también podemos decir, que para cada hipérbola tendremos la relación, en donde, (a) será la longitud del semieje transverso, en cuanto (b) representará el valor del semieje conjugado y a lo que se refiere a (c) es la distancia del centro a cada uno de los puntos fijos a los cuales hemos denominados focos, esto hace que tanto a, b y c estén relacionadas con la siguiente igualdad:

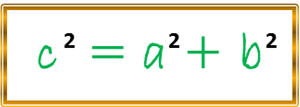
Entonces, conociendo esta relación podemos despejar (b) para seguir con la reducción de nuestra ecuación, la cual represente el lugar geométrico de una hipérbola según las condiciones inicialmente descritas, por lo tanto, seguimos:

Entonces, pudimos determinar la ecuación de la hipérbola con centro en el origen del plano coordenado y cuyo eje focal coincide con el eje de las X, por lo que las coordenadas de sus focos son F(c , 0) y F´(-c , 0) , es necesario expresar que en el caso de tener las condiciones para las cuales el eje focal coincida con el eje de las Y, y cuyos focos tengas las coordenadas F(0 , c) y F´(0 , -c) ; la ecuación a utilizar será la siguiente:

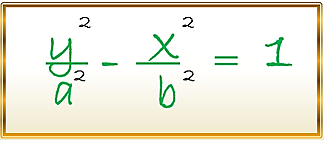
Para el análisis de esta importante curva también debemos tener en cuenta, que para cada hipérbola, la distancia o la longitud que representa cada uno de sus lados rectos debemos calcularlas utilizando la siguiente expresión:

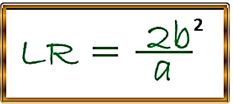
En cuanto a la excentricidad de la hipérbola, como la describimos en la pasada publicación de la elipse representada por la letra (e) y la podemos definir mediante la razón o cociente c/a, pero para el caso de esta curva dicho valor será mayor que la unidad, debido a que el valor de c > a , por lo tanto, su expresión algebraica es la siguiente:

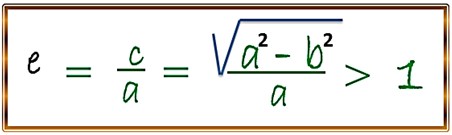
Para determinar esta ecuación tomaremos en cuenta la condición, en donde, el centro de esta curva no es el origen del plano coordenado y sus ejes serán paralelos a los ejes del referido plano, por lo tanto, tendremos que para este análisis, el centro de la hipérbola estará representado por el punto cuyas coordenadas serán (h , k) y su eje focal puede ser paralelo tanto al eje de las X como a de las Y, utilizaremos la siguiente figura para realizar tal determinación.

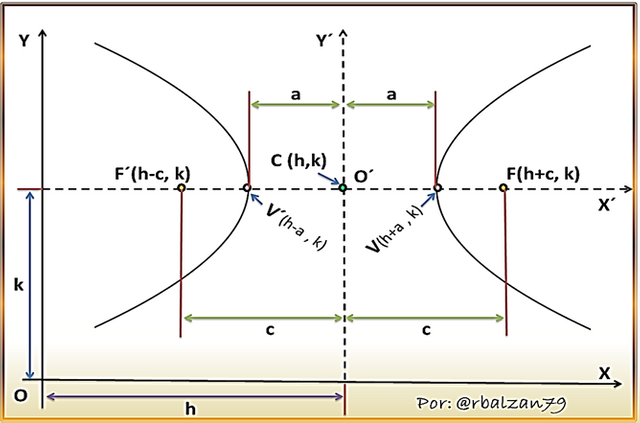
Podemos observar con facilidad que trasladamos los ejes coordenado a nuestro nuevo origen (O´), es decir, al centro de la hipérbola cuyas coordenadas son (h , k) según la condición antes descrita, además también podemos notar que el eje focal de la curva es paralelo al eje de las X, por lo tanto, nos podemos apoyar tanto en anterior figura como en la primera ecuación de la hipérbola, la cual, su eje focal coincide con el eje de las X, y su centro con el origen del plano coordenado, claro está, lo haremos con referencia a los nuevos ejes X´ y Y´, por lo tanto, tenemos:

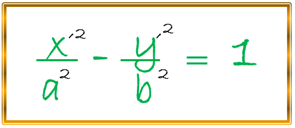
De la misma forma como lo realizamos para la elipse y la parábola podemos deducir en la expresión anterior, nuestra nueva ecuación relacionada a los eje iniciales u originales, es decir, X , Y; por lo que mediante la utilización de las conocidas ecuaciones de transformación podemos expresar lo siguiente:

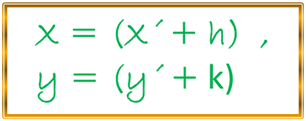
Luego al despejar X´ y Y´ tenemos:

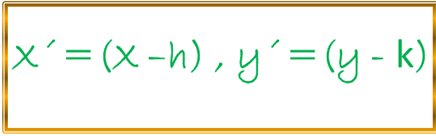
Al sustituir estos valores de X´ y Y´ en la primera ecuación de la hipérbola para el caso horizontal obtenemos:

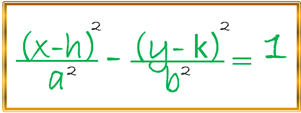
De esta manera determinamos la segunda ecuación de una hipérbola cuyo centro tiene coordenadas (h , k) y su eje focal paralelo al eje de las X, para el caso, en donde, el eje focal sea paralelo al eje (Y) la ecuación es la siguiente:

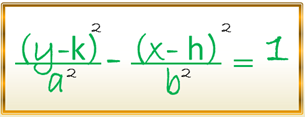
Con estas dos últimas expresiones consolidamos la segunda ecuación de la hipérbola para el caso horizontal y vertical, en donde, la relación entre los valores de a, b y c ; es de la misma forma que en la primera ecuación, de igual manera ocurre con la longitud de cada lado recto, así como para la excentricidad.

Es importante tener en cuenta que mediante el análisis de una expresión o ecuación general de la hipérbola, si los coeficientes A y C son diferentes en sus signos, entonces, dicha ecuación representará una hipérbola, bien sea, con eje focal paralelo al eje de las X o al eje de Y, es decir, a cualesquiera de los ejes del plano coordenado, por lo tanto, mostramos esta forma general:

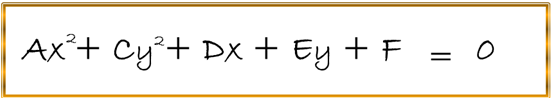
Ejercicio

Según la siguiente expresión de forma general:

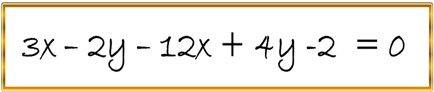
Analizar su lugar geométrico y luego hallar:

a.- El centro (h , k) de la elipse.
b.- Longitud del eje transverso y eje conjugado.
c.- Coordenadas de los focos.
d.- Coordenadas de los vértices.

La anterior ecuación general, debemos transformarla de la forma canónica para cualquiera de los dos casos (horizontal o vertical), es decir, tener las siguientes formas:

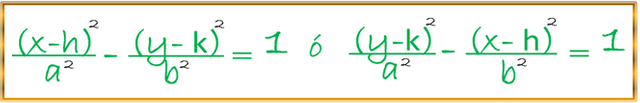
Iniciamos completando los cuadrados de cada una de las variables:

Ahora con esta ecuación podemos encontrar cada uno de los elementos solicitados en nuestro enunciado.

En nuestra actualidad, para nadie es un secreto que el inmenso o infinito espacio que nos rodea se encuentra repleto de secciones cónicas, aquellas descartadas por los matemáticos en sus inicios, sin embargo, ellas volvieron para retomar el lugar que les correspondían, es decir, estar al servicio de la humanidad, en la pasada publicación observamos la importancia de la elipse en la determinación de importantes leyes las cuales transformaron por completo tanto el campo de la ciencia como cualquier área que tenga que ver con nuestro desarrollo intelectual y por lo tanto social, es uno de los propósitos de este artículo, poder ir más allá de la utilización de estos valiosos conocimientos en nuestras aulas de clases, ya que es necesario despertar en cualquier persona el interés hacia nuestra ciencia, en todo su esplendor, y sabemos que las matemáticas nos ha permitido desarrollarnos exponencialmente en cualquier lugar o área de nuestras vidas.

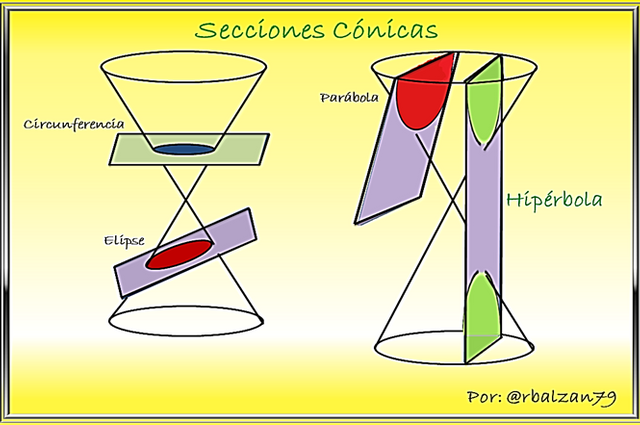
En esta oportunidad hablaremos y resaltaremos la importancia de otras de estas secciones cónicas, la hipérbola, la cual analíticamente podemos decir, que es el lugar geométrico de aquellos puntos los cuales comprueban una determinada relación de distancias, como claramente lo pudimos hacer en la conformación de la primera y segunda ecuación ordinaria o canónica de esta curva, esta característica es lo que nos ha permitido utilizarla o aplicarla en diversos campo de nuestra cotidianidad, estas figuras cónicas históricamente deben su típico nombre a las distintas secciones obtenidas de un cono circular recto, como podemos observar en la siguiente figura:

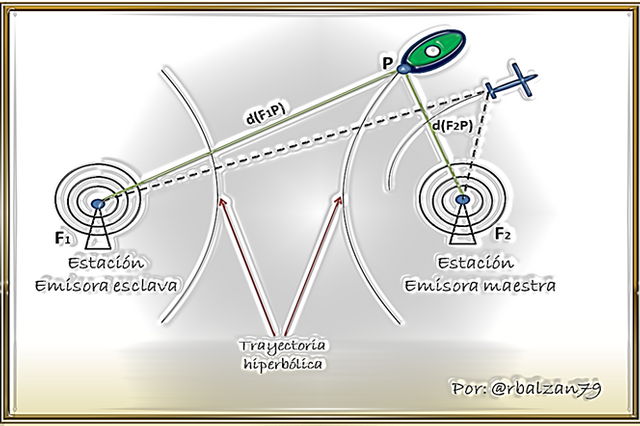
Unas de las aplicaciones de esta figura consisten en la ubicación o posición de un barco en alta mar o de un avión en el espacio aéreo, mediante el sistema de comunicación por radio denominado LORAN (abreviatura en inglés de long range navigation), es decir, navegación de largo alcance, este sistema es uno de los tantos métodos que les proporciona a los navegantes o pilotos establecer la posición de su embarcación o de su avión respectivamente, esto se logra partiendo de la diferencia de recepción de las señales de radio las cuales se originan de dos emisores ambos sincronizados y separados uno del otro, por lo que este sistema emisor se conforma por dos estaciones, una maestra y la otra esclava o secundaria, en donde dicha estación maestra transmite una pequeña señal en lapsos de 0.05 segundos y dicha señal es repetida por la estación esclava, esta última señal es controlada por radio desde la estación maestra, 0,001 segundos después, ambas señales son recibidas por el barco o el avión, las cuales se amplifican y se observan como pequeñas ondas sobre una pantalla, es importante resaltar que los respectivos circuitos del receptor están instalados de manera que la distancia que existe entre las señales correspondan a la diferencia de tiempo de recepción de las señales originadas en ambas estaciones, esto entonces hace que la curva que observa el navegante o piloto sea una hipérbola y cuyos focos lo representan ambas estaciones emisoras, como podemos observar en la siguiente figura.

El físico y químico Irlandés Robert Boyle, enuncia la ley de los gases, la cual expresa que a temperatura constante, PV = k, la gráfica sobre el comportamiento de esta ecuación es una hipérbola, como se muestra a continuación:

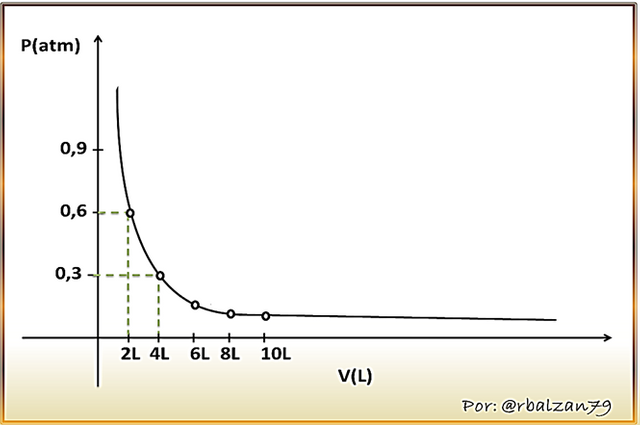
En la anterior imagen podemos observar la relación gráfica entre P y V a temperatura constante, en donde, notamos que el volumen de un determinado gas se incrementa al doble cuando reducimos la presión a la mitad.

En cuanto a la astronomía, los cuerpos celestes extraños (como cometas) al sistema solar y los cuales son atraídos por el sol, describen un recorrido en forma de hipérbola, esto permite que podamos calcular su trayectoria con extraordinaria precisión.

De esta forma podemos encontrar innumerables aplicaciones de esta sección cónica llamada hipérbola, áreas importantes para nuestro desarrollo social como la arquitectura, ingeniería, entre otras, estas curvas siempre tendrán una utilidad en las distintas actividades del ser humano.

1.- De igual forma que lo hicimos para el análisis de las curvas anteriores, comprobamos que siempre es muy necesario los conocimientos previos los cuales hemos ido obteniendo y compartiendo desde las curvas iniciales, muchos aspectos relevantes que destacar durante el estudio de esta figura cónica, podemos resaltar que la geometría analítica plana a través de una expresión general de segundo grado puede representar a tales secciones cónicas, como lo pudimos demostrar en el ejercicio planteado, en donde, obtuvimos la ecuación canónica que representa el lugar geométrico de una hipérbola de tipo horizontal, por lo que es necesario recomendar la transformación de este tipo de forma general a la forma más sencilla como la canónica, ya que podemos de manera objetiva visualizar con gran facilidad el tipo de cónica o curva que tenemos que analizar.

2.- Es importante la determinación de las ecuaciones más fundamentales de una cónica o curva como la hipérbola, debido a que de allí comienza todo tipo de interpretación relacionada a cualquiera de estas secciones cónicas, y en este artículo lo pudimos observar, logramos encontrar el lugar geométrico de la misma y comprender cada uno de los elementos que pertenecen a dicha curva, elementos vitales como los puntos fijos llamados focos, eje focal, eje transverso y conjugado, entre otros, los cuales son de gran importancia para el entendimiento de las expresiones algebraicas que dan lugar a las ecuaciones ya descritas.

3.- Debemos resaltar de igual forma el esencial análisis realizado al importante aspecto de movilidad ofrecido por la geometría analítica, y que gracias a aplicaciones como PhotoScape logramos tal cometido, ya que pudimos demostrar que realizando el análisis desde dos puntos distintos de la curva obtuvimos el mismo valor constante (2a), reflejado en la definición de la hipérbola, esto acompañado con las imágenes sin dudas nos permiten mejorar y facilitar el entendimiento de los conocimientos matemáticos, los cuales sabemos, que en muchas ocasiones cuesta lograr tal objetivo, pero estamos hablando de ciencia educativa y por lo tanto todo esfuerzo vale la pena y tendrá sus resultados positivos, ya que siempre debemos tener presente que a través del campo científico y la compresión de cada una de sus ramas en cualquier área y forma que se encuentren, será posible poder seguir sobreviviendo en este planeta.

4.- Hablar de matemática es hablar del pilar fundamentar de la humanidad, y sabemos que nos ha permitido poder nutrir a las distintas áreas del campo de la ciencia, así como a cualquier tipo de área que nos ha permitido nuestro bienestar social, por lo tanto, resaltar la utilidad de unas de las curvas cónicas como la hipérbola es vital para profundizar e incentivar tanto al conocimiento de las misma como a la valoración de tales aprendizajes, ya que estas cónicas cohabitan con nosotros desde tiempos muy remotos y a veces le restamos importancia a sus extraordinarias aplicaciones, las cuales serán parte de nosotros por siempre y por ello lo necesario de poderlas comprender lo más posibles.

5.- En el desarrollo del presente artículo logramos tres aspectos generales de gran importancia, uno, enfocados a la determinación de las ecuaciones fundamentales de la hipérbola para poder encontrar su lugar geométrico, dos, durante dicha determinación también pudimos resaltar y realizar el movimiento de un determinado punto, el cual desde dos diferentes ubicaciones nos permitió consolidar el aspecto conceptual de esta cónica, tres, cerrando con algunas de las aplicaciones de la hipérbola en nuestras actividades cotidianas, característica que tiene muchísimos aspectos intrínsecos vitales para el apasionamiento tanto por las matemáticas como por cualquier otras de las ramas de la ciencia, bien sea de manera educativa o experimental.

Hasta otra oportunidad mis apreciados lectores de steemit, en especial a los miembros de la gran comunidad de #STEM-Espanol, los cuales reciben el apoyo de otras dos grandes comunidades como los son #steemstem, #utopian-io , por lo cual recomiendo ampliamente formar parte de este hermoso proyecto, ya que resalta la valiosa labor de la academia y del campo científico, pero sobre todo, por el gran respecto, dedicación y ayuda para sus miembros.

Nota: Todas las imágenes fueron elaborados usando las aplicaciones Paint, Power Point, GeoGebra y el gif con PhotoScape.

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.

[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.

[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.

[4] Alegría Pedro. Las cónicas y sus aplicaciones.pedro.alegrí[email protected].

[5] Casanova Graciela Monica. Cónicas Por siempre Cónicas. Instituto Superior “FUNDACIÓN SUSUKI”. Marzo 2009.

[6] Bohórquez Salvador, A.; González Flores, J.M.; Haro Moreno J.M.; Mateos Ortiz, F.J. Idea de lugar geométrico en el plano, Cónicas. Universidad de Sevilla, 2013-2014.

[7] Raymond Chang, Williams College. Séptima Edición. Editorial McGrawHill. México, 2002.