La Elipse//Determinación de su ecuación y su gran utilidad en el amplio campo del intelecto humano

Continuando con la temática geometría analítica plana, en donde, seguimos dando importantes pasos para la comprensión analítica de las matemáticas, en esta oportunidad estudiaremos a la elipse, por lo tanto, conoceremos la determinación de sus ecuaciones más fundamentales, así persistimos con el análisis detallado de las ecuaciones y los lugares geométricos de una curva específica, determinando de esta manera sus propiedades particulares, hasta ahora hemos estudiado a la línea recta, circunferencia y la parábola, representando de estas tres líneas o curvas un aspecto de importante valor para cualquier estudiante o profesional en cualquier área donde se desempeñe, pero el objetivo es seguir brindando el aspecto analítico de importantes curvas para la mejor interpretación y comprensión de las mismas.

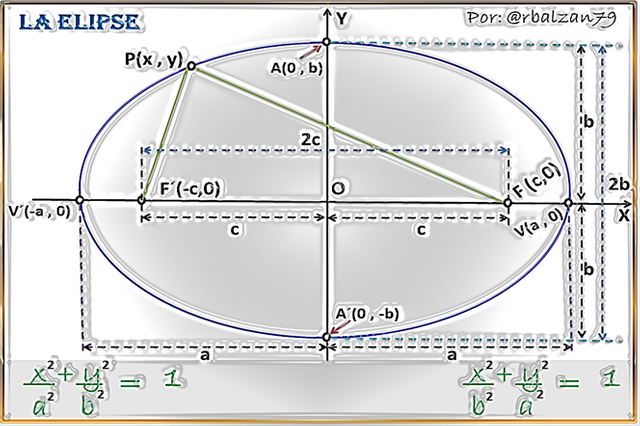
Para la definición de esta importante curva, podemos expresar que es un lugar geométrico formado por el movimiento de un determinado punto en el plano, en donde, tenemos presente a dos puntos fijos llamados focos y cuya suma de las distancias a estos puntos será siempre equivalente a una constante, la cual, es mayor a la longitud que exista entre tales puntos fijos.
Para una mejor comprensión de la definición de esta importante curva, la elipse, consideremos la siguiente figura para poder determinar el aspecto conceptual desde la visión analítica de la geometría plana, por lo tanto, tenemos:


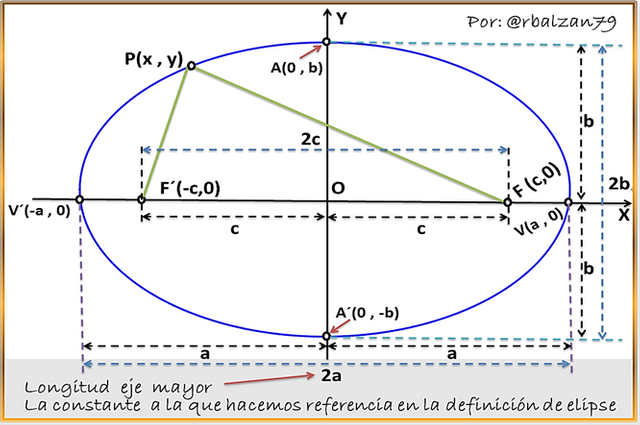
Para la determinación de esta ecuación tomaremos en cuenta la condición en donde, esta curva tiene su centro en el origen del plano coordenado y su eje focal coincide con el eje X, por lo tanto, los respectivos focos se encuentran sobre dicho eje, por lo tanto, el centro está representado por el origen (O) y es el punto medio del segmento formado entre los focos FF´, entonces, las coordenadas tanto para F son (c , 0) y para F´ son (-c , 0) resaltando que el valor de (c) será una constante positiva, como podemos observar en la siguiente figura:
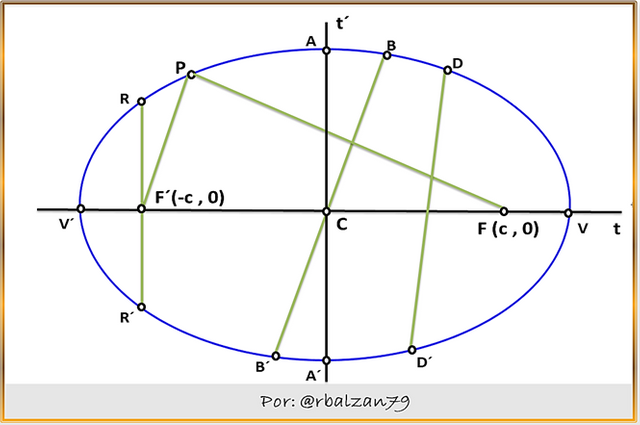
Si tenemos cualquier punto P(x,y) de dicha curva, podemos expresar según la definición de la elipse antes descrita, que el mencionado punto deberá satisfacer la siguiente condición geométrica:
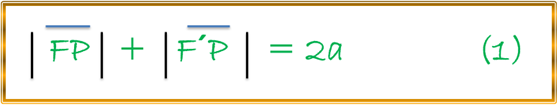
El valor de (a) siempre será una constante positiva y mayor que el valor de la constante (c), por lo tanto, recordemos la fórmula de la distancia entre dos puntos en el plano para poder verificar la anterior relación o igualdad (1):
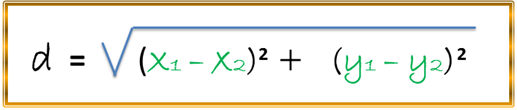
Aplicamos esta fórmula de la distancia a FP y F´P:

Siguiendo con la determinación de la ecuación de la elipse según condiciones geométricas descritas, procedemos a resolver la relación (2), para ello es conveniente pasar nuestro segundo radical al otro lado de la igualdad, y realizamos los procedimientos correspondientes, como elevar al cuadrado toda la expresión para luego simplificar términos iguales como se muestra a continuación:

Continuamos desarrollando la última expresión obtenida, con la finalidad de simplificarla lo más posible, para ello elevamos al cuadrado nuevamente ambos elementos de nuestra igualdad deducida anteriormente como se muestra a continuación:
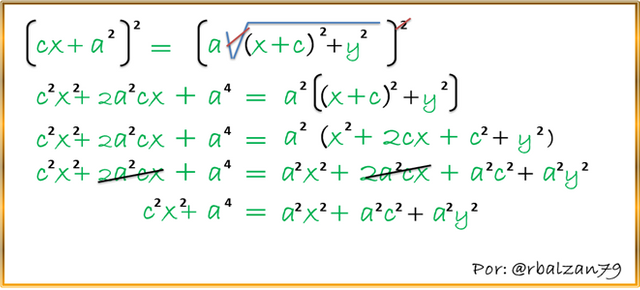
Antes de seguir es importante resaltar que para cada elipse tenemos que el valor de (a) representa la longitud del semieje mayor, en cuento al valor de (b) es la longitud del semieje menor, por lo que dichos valores están sujetos a la siguiente relación:
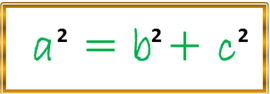
Conocida esta relación la utilizamos para seguir reduciendo nuestra ecuación analizada de una elipse con las condiciones geométricas ya descritas con anterioridad, por lo que continuamos de la siguiente forma:

Podemos expresar que encontramos la ecuación de la elipse cuyo centro es el origen del plano y su eje focal coincide con el eje de las X, donde su distancia focal es igual a 2c y cuya cantidad constante 2a, pero si tenemos, que nos presentan otras condiciones, en donde, el eje focal de una elipse coincide con el eje de las Y, por lo tanto, los focos tendrán coordenadas (0 , c) y (0 , -c) la ecuación de la elipse que representa estas condiciones será:
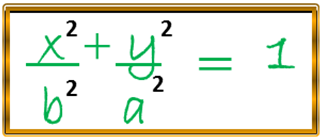
Tenemos que considerar que para la longitud de los lados rectos de la elipse, podemos utilizar la siguiente expresión:
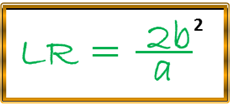
También es importante resaltar la excentricidad de una elipse, la cual representa el grado de aplastamiento de dicha curva cerrada, la misma representa uno de los más destacados elementos a considerar durante su análisis, por lo tanto, la podemos definir como la razón o el cociente c/a y este elemento lo simbolizamos con la letra (e), tenemos la siguiente expresión:
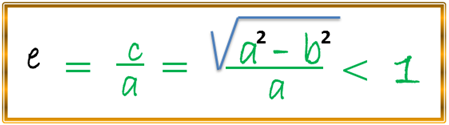

Para este análisis tomaremos en cuenta que el centro de una elipse está representado por el punto cuyas coordenadas son (h , k) y su eje focal paralelo al eje de las Y, nos apoyaremos en la siguiente figura para la determinación de esta ecuación.
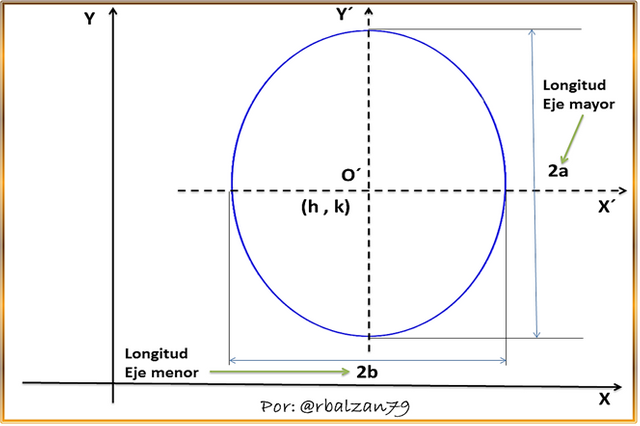
En la anterior figura podemos notar que hemos trasladado los ejes coordenados a nuestro nuevo origen, es decir, al centro cuyas coordenadas son (h , k) de dicha elipse, por lo que podemos seguir la relación de la ecuación de la elipse para el caso vertical determinada anteriormente, en donde, el eje focal de esta curva coincide con el eje de la Y, y su centro con el origen del plano coordenado, pero lo haremos en este caso con referencia a los nuevos ejes X´ y Y´, por lo tanto, tenemos:
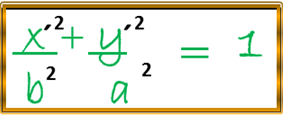
Mediante la anterior expresión podemos deducir nuestra nueva ecuación relacionada a los ejes originales, es decir, X , Y utilizando las conocidas ecuaciones de transformación, las cuales las implementamos en la pasada publicación sobre la parábola en donde podemos escribir lo siguiente:
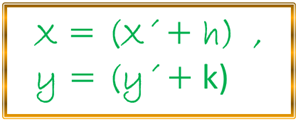
Despejando X´ y Y´ obtenemos:
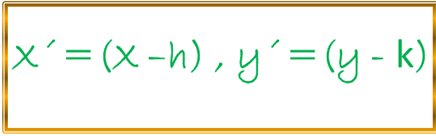
Al remplazar dichos valores de X´ y Y´ en la primera ecuación de la elipse para el caso vertical tenemos:
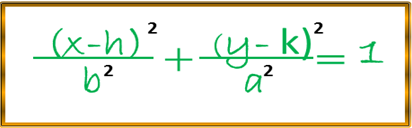
De esta manera obtenemos nuestra ecuación de la elipse cuyo eje focal es paralelo al eje Y, y con centro (h , k). Para el caso, en donde, el eje focal sea paralelo al eje X y centro un punto de coordenadas (h , k) , la ecuación para estas condiciones será:
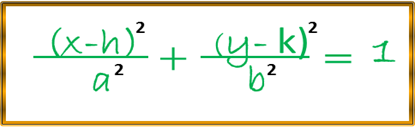
Estas últimas expresiones la denominamos por lo general la segunda ecuación ordinaria de la elipse, en donde, los valores tanto de a, b y c están igualmente vinculados a la relación descrita en la primera ecuación ordinaria de la elipse, también encontramos que la fórmula para la longitud de los lados recto es la misma, así como la relación de la excentricidad de la elipse.
Ejercicio
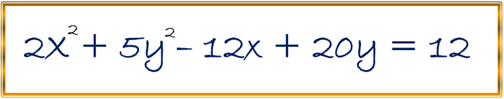
Hallar:
a.- El centro (h , k) de la elipse.
b.- Longitud del eje mayor y menor.
c.- Coordenadas de los focos.
d.- Coordenadas de los vértices.
e.- Excentricidad.
Primeramente debemos recomendar que siempre que tengamos este tipo de expresiones es aconsejable transformarla en la forma de la ecuación canónica de una curva, elipse para este caso, por lo tanto, recordemos dichas ecuaciones para tales condiciones:
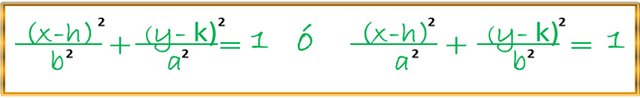
Comencemos con los procedimientos algebraicos para la transformación de dicha expresión, iniciando con la asociación de las variables de igual literal.
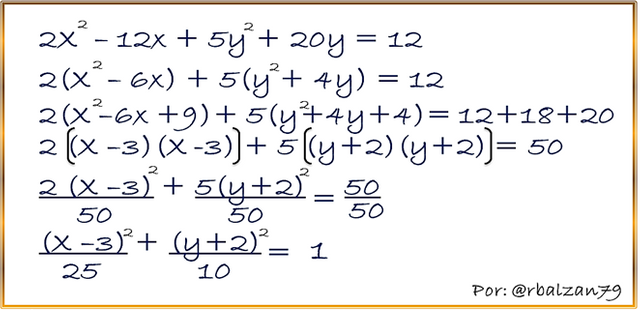
Observamos que en la ecuación canónica encontrada el denominador mayor corresponde a la variable X, por lo que el eje focal de nuestra elipse coincide con el eje de las X, por lo tanto, la relacionamos con la siguiente ecuación:
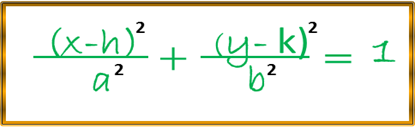
Con esta ecuación podemos encontrar cada uno de los elementos solicitados en nuestro enunciado.


En nuestro desarrollo como humanidad pensante e intelectual, muchas invenciones en matemáticas, no representaron en sus inicios gran importancia para la determinación de extraordinarias formulaciones a futuro, por lo que pasaron desapercibidas durante largo tiempo de nuestra historia, podríamos decir que un claro ejemplo lo representaron las curvas denominadas cónicas en las cuales encontramos a la que estamos analizando en este artículo, es decir, la elipse, estas cónicas incluyendo a la elipse tienen innumerables aplicaciones en distintas áreas de la ciencia, en cuanto, a nuestra elipse, nadie pudo pronosticar en sus inicios que posteriormente sería utilizada para poder explicar el movimientos de los planetas de nuestro sistema solar, debido a los trabajos realizados por el astrónomo alemán Johannes Kepler pudo resolver el gran enigma de tales movimientos planetarios, el cual, descubrió para ese entonces que el planeta denominado Marte tenia movimientos en forma de órbita elípticas y que el gran astro de nuestro sistema, es decir, el sol, se encontraba situados en uno de los focos de dicha cónica elíptica, en nuestra actualidad es claramente conocido que este comportamiento de Marte descrito por Kepler se originan en los demás planeta del mencionado sistema solar, pero este aporte no se quedó aquí, ya que gracias a estos estudios brindador por Kepler, el gran Sir Isaac Newton consolidó y completó las referidas leyes sobre el movimiento, y dio a conocer sus tan famosa leyes, la primera ley la de inercia, la segunda ley la cual expresa que un cambio del movimiento será proporcional a la fuerza que se aplica, la tercera ley basada en el importante principio de acción y reacción, aquí está el enlace de una de mis publicaciones donde se hace referencia a tales leyes Dinámica, así como otra de sus impresionantes leyes la de gravitación universal.
Uno de los más novedosos inventos por la humanidad como lo son los satélites, estos igualmente describen una órbita elíptica, algunos de mayor o menor excentricidad que otros, estas órbitas elípticas es lo que les permite poder repetir el ciclo de órbita. Como ya describimos, la excentricidad está relacionada al grado de aplastamiento de esta figura cónica, en donde, es muy importante tener en cuenta que cuando tenemos una excentricidad que sea igual a cero (0), dicha figura representará un círculo perfecto, por lo tanto, mientras mayor sea la excentricidad el grado de aplastamiento será mayor en la elipse, como expresamos las órbitas de los planetas son de forma elípticas, las cuales tienen una pequeña excentricidad, por ejemplo, el planeta tierra es de 0,017.
Podemos considerar que en la tercera ley de Kepler, la ley armónica, en donde, describe que los cuadrados de los períodos orbitales de los planetas tienen una relación proporcional al cubo de sus referidas distancias medias al sol, es decir:
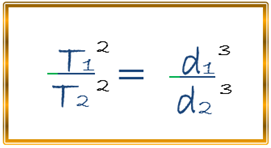
En donde, T1 y T2 representan cada período orbital y en cuando a d1 y d2 son las distancias con los que los planetas orbitan del sol, en el caso de nuestro sistema solar, debemos resaltar que tal ecuación será pertinente siempre y cuando consideremos a las masas de los objetos a estudiar como despreciables esto en relación al cuerpo central al cual orbital, podemos considerar el siguiente ejemplo, para el cual ponemos en práctica la anterior fórmula:
Calcular la distancia del Sol y la Tierra, de ambos sabemos que su período orbital es de 1 año, para este análisis necesario es contar con una referencia ya establecida, la cual pudiera ser la del planeta Marte, ya que el mismo, al igual que el planeta Tierra órbita al Sol, y lo hace con un período orbital de 1,8809 años y una distancia del mismo de 1,5237 U.A. (Unidad Astronómica) aproximadamente.
Aplicando la anterior fórmula, tenemos:

De esta manera obtenemos la distancia solicitada, de esta forma podríamos hacer con los demás planetas del sistema solar.
Es importante tener en cuenta que al calcular el semieje, como veremos en la siguiente figura, encontramos la distancia entre los centros de los cuerpos relacionados.
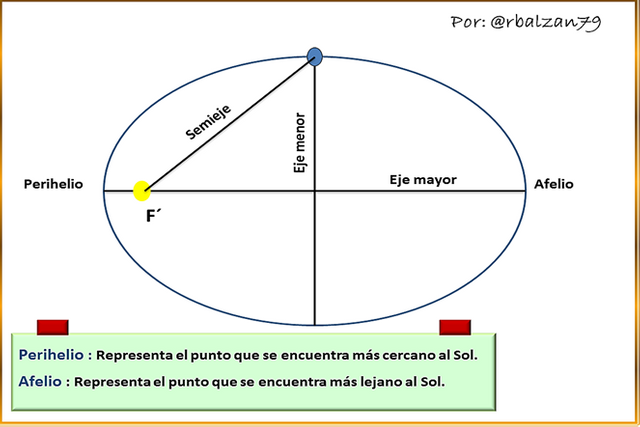
Podemos calcular tanto el perihelio como el afelio, pero debemos tener el dato de la excentricidad, en este caso el del planeta tierra, el cual ya lo expresamos con anterioridad, y es igual a, e = 0,017, por lo tanto, tenemos:

1.- De igual forma que para el análisis de las gráficas anteriores, notamos que siempre es necesario los conocimientos previos obtenidos de las curvas iniciales, por lo que vamos articulando el aprendizaje de manera analítica y práctica de las mismas, lo cual representa un fundamento esencial para la comprensión de la geometría analítica plana, así como en cualquier área de las matemáticas, ya que la debida interpretación del saber matemático nos conducirá a un mejor dominio al momento de aplicarlos en distintos ámbitos de nuestro desarrollo intelectual, sobre todo en el campo académico, así como en cualquier espacio del saber humano.
2.- En el presenta artículo realizamos el estudio de la elipse determinando sus ecuaciones más fundamentales, por ello, las denominamos ecuaciones de la forma canónica, y con ellas logramos encontrar el lugar geométrico y comprender cada uno de los elementos que pertenecen a dicha curva, elementos esenciales como los puntos fijos llamados focos, eje focal, eje mayor y menor, entre otros, los cuales son de gran importancia para el entendimiento de las expresiones algebraicas que dan lugar a las ecuaciones ya descritas.
3.- Es importante tener presente que siempre será de gran ayuda poder reducir cualquier ecuación de una elipse a su forma canónica, ya que de esta manera podríamos fácilmente comprobar su posición relación con respecto a los ejes coordenados, esto lo podemos lograr al comparar los denominadores de las variables X^2 y Y^2, para lo cual, el mayor denominador lo relacionamos con la variable que corresponda al eje coordenado, con el cual el eje focal de la elipse tiene coincidencia, es decir, dependerá a simple vista quién tenga de las dos variables el mayor denominador para poder saber con cual eje coordenado del plano va a coincidir el eje focal de una determinada elipse.
4.- La utilidad de las curvas cónicas ha representado un hecho de vital importancia en la evolución de muchas ramas de la ciencia, con la determinación de extraordinarias fórmulas y planteamientos los cuales han revolucionado el área del saber de la humanidad, como pudimos observar con el estudio realizado por el astrónomo Kepler y el gran Sir Isaac Newton, personajes históricos y además de gran renombres dejaron sus profundas hullas en nuestro gran desarrollo, debido a sus inmortales leyes las cuales revolucionaron extraordinariamente de manera positiva a ramas de la ciencia como la física, astronomía, química, por nombrar algunas, contando con los conocimientos implementados por cónicas como la elipse, las cuales son innumerables las áreas que en la actualidad aún sigue impactando positivamente la aplicación del saber de la curva denominada elipse.
Nota: Todas las imágenes fueron elaborados usando las aplicaciones Paint, Power Point.

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.
[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.
[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.
[4] Alegría Pedro. Las cónicas y sus aplicaciones.pedro.alegrí[email protected].
[5] De Bernardini Enzo. Leyes de Kepler. Astronomía Sur. Http://astrosurf.com/astronosur, UNLP, 1998.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Una forma muy educativa, dinámica y explicita la que nos brinda el compañero @rbalzan79 en su publicación acerca de la elipse, y que con su apoyo en las aplicaciones que esta tiene puede incentivar a los alumnos de geometría a que valoren el estudio de la geometría analitica y la importancia que esta tiene en la ciencia y la Ingeniería. Saludos y estaremos a la espera de más contenido acerca de esta temática. Saludos
Hola @rbalzan7, un aporte muy completo que no sólo se queda en la teoría vinculada al concepto sino que haces un amplio recorrido por las aplicaciones del concepto de la Elipse en otros escenarios científicos de los cuales hay sobrada evidencia. Considero que de la misma manera es educativo, es decir, yo recomendaría esta lectura a estudiantes de Educación mención Matemática, en tanto que si queremos que ellos respondan la típica pregunta de los estudiantes de bachillerato ¿Para qué sirve la Matemática? tenemos que empoderarlos con saberes dirigidos a ampliar sus conocimientos de la aplicación de esta importante ciencia tanto en la vida cotidiana como en otros ámbitos científicos, esto es, si sólo le enseñamos lo teórico y práctico sin propósito seguiremos teniendo en las aulas del país y del mundo estudiantes que no quieran estudiar Matemática o carreras vinculadas porque no saben para que sirve ni en donde se aplica. Te felicito por tu elaborado y detallado aporte, saludos fraternos!!
Es bastante interesante lo que aportas en el contenido, sin embargo estoy de acuerdo con @reinaseq. Es importante poder conocer algunas aplicaciones al respecto, aunque lo mencionas es bueno profundizar un poco más. De resto excelente contenido @rbalzan79
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias por su importante apoyo. Saludos hermanos.
Hi @rbalzan79!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV