Inequality: Always, sometimes or never?
"Always, sometimes or never?"
"Is it always true, sometimes true or never true?"
These are questions that we should ask for everything in life, including mathematics. However, many students are accustomed to a fixed way of doing things, a fixed set of procedures to follow, a fixed type of solutions to problems. They will coast along until they encounter the following type of problem.
"What?!? I am used to seeing equations like 3 x + 1 = 7 which have one answer, and equations like x² = 9 which have 2 answers and inequalities like 2 x - 1 > 5 which has a range of answers, but not those above!?!"
Certainly so. This question is a little bit more challenging. But do not panic. Try to look for patterns. Observe that can be split up as
using the difference of squares
formula, with
and
.
Remembering that which is an identity (so it always true), we end up with a silly statement like
which is never true. So there is no solution for part (a).
For part (b) we proceed similarly.
We end up with a the statement like which is always true. Everything is always greater than or equal to itself. Even though the "greater than" part is not true, the "equal" part is definitely true. So the statement is considered as true, for whatever value of theta you care to substitute in it. That means theta can be any real number. The solution set is the set of all real numbers.
Now for the clincher!
Again we proceed as in parts (a) and (b) but note that both and
are equal to
, which makes the Right Hand Side zero. On the Left Hand Side, note that
, so the question now becomes when is
greater or equal to zero.
You may want to use the ASTC or "All Science Teachers are Crazy" mnemonic to help determine the quadrants where the cosine is positive or negative. For me, I prefer to consider the fact that the cosine is just the x-coordinate on the unit circle, so the cosine is positive on the right two quadrants (quadrants 1 and 4). We know that is non-negative from -90 degrees to 90 degrees, or from
to
radians. But we can go round and round the circle, clockwise and/or anti-clockwise indefinitely to get other solutions. This means we keep on adding or subtracting 360 degrees or
radians. It turns out that there is a pattern.
must be from
to
, where k is some integer. Dividing the inequality through by 2 gives our final answer.
In conclusion
When solving inequalities or equations, we should consider the possibility that the it may always be true, or never be true, or sometimes true.
I hope you have learned something solving these challenging inequalities.
Image Credits
The first picture was derived from Pixabay, while the rest are all my own work.
Announcements
You might also want to read my recent articles:
Integral of 1/sqrt(e^2x+1) (Trigo Approach)
Simplifying Roots
"Singapore Math": The Ribbons Problem from PSLE 2017
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds

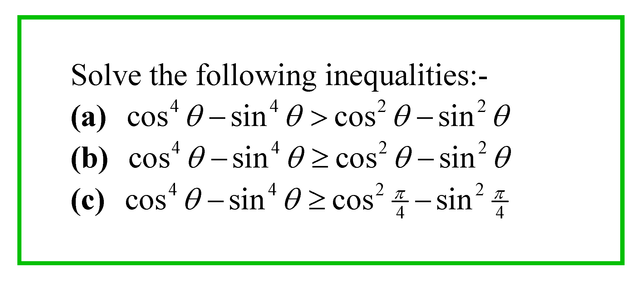
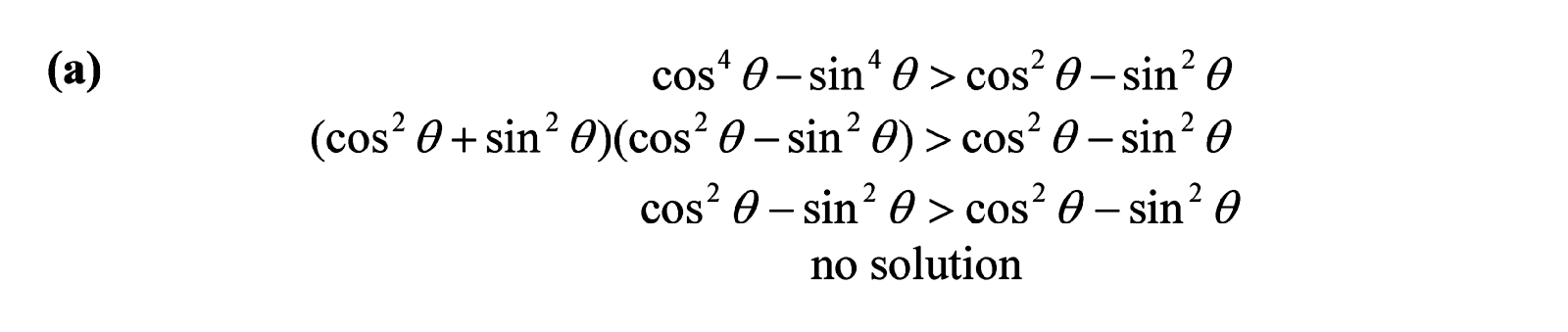
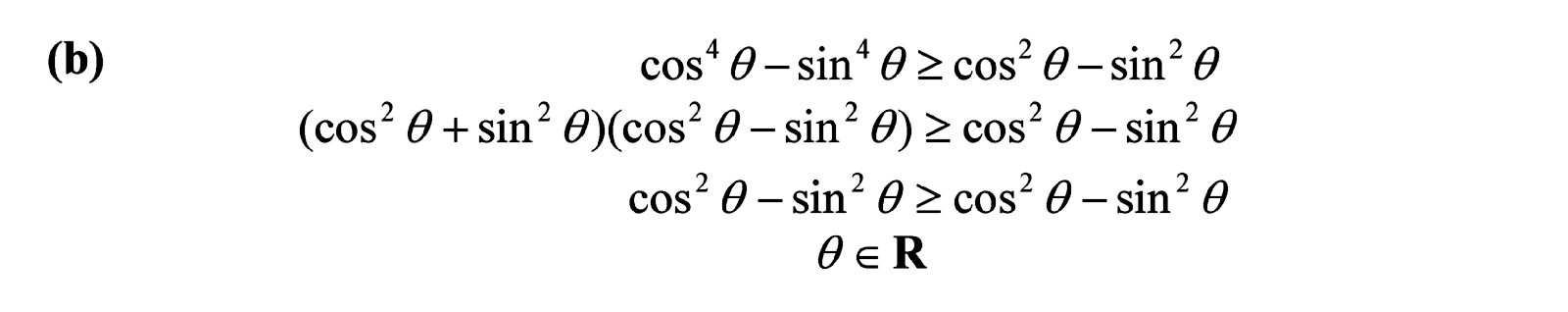
img credz: pixabay.com
Nice, you got a 7.0% @minnowbooster upgoat, thanks to @tradersharpe
Want a boost? Minnowbooster's got your back!
The @OriginalWorks bot has determined this post by @tradersharpe to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
For more information, Click Here!
Special thanks to @reggaemuffin for being a supporter! Vote him as a witness to help make Steemit a better place!
This post has received a 1.44 % upvote from @booster thanks to: @tradersharpe.
@driva has voted on behalf of @minnowpond.
If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.
Your thinking is better. Actually who have energy & wisdom is creative.
Dang yeah, that stuff is what many students struggle with. 🐐
Mathematical terms & condition very tough.
If only I had you around when I was in school! @tradersharpe ;)
@cmtzco has voted on behalf of @minnowpond.
If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.
hi frineds nice post and give vote good
https://steemit.com/steemstem/@light-o-trix/defense-strategy-and-capabilities-development-across-the-globe-is-it-a-threat-for-the-human-race