The Napkin Ring Paradox

if you've ever been to a wedding, or maybe a fancy dinner, you would probably have noticed those rings within which napkins are placed. Yes, Napkin Rings.

That is a key part of our topic for today. But then, you may have also noticed the word paradox in the title, and even though weddings (and marriages) can be paradoxical lol, yet we're gonna mostly gonna be talking Math :D (and Geometry to be more precise).

Napkin Ring

What is the Napkin Ring shape?

The Napkin Ring shape originates from a sphere, that has been cored out to cut off a cylinder shape out of it. This is due to the purpose of Napkin rings, to essentially hold napkins within.
Napkin rings were actually invented around the 1800's as part of the European Bourgeoisie, appearing initially in France, and then spread all across the world, and they brought us this following cool paradox ..

Geometric Shape - Side and Lateral Views

So what is this Napkin Ring paradox?

The paradox actually relates to the volume of those napkin rings, and can basically be summarized into:

Any two napkin rings, with the same height, will have the same volume, regardless of the size of their original spheres.

I.e., if you have a sphere that is the size of a small pebble, and another that is the size of a watermelon, cutting off equally tall napkin rings from both of these objects, both will have the exact same volume. The smaller one would actually have a thicker ring, but both will have the exact volume.

If you want to even think on a bigger scale, maybe extreme, consider Earth as the larger sphere, coring it out and creating a napkin ring out of it, with the same height of the pebble, would also yield the same volume -
the circumference of the Earth napkin ring would actually be our entire planet though compared to few centimeters for the small pebble, so that's a big too big to hold lol, yet same volume.

See illustration below of napkin ring with same height yet different circumference (and hence originating sphere)

Cut napkin ring animation with equal height

So that is at the core of this paradox, and yes it definitely sounds counter-intuitive, so let's get on to the Maths to prove it :)

Let's prove it! (TL;DR: permission granted to skip to The Juice section, yet you'll miss out on the fun)

The proof actually relies on Cavalieri's Principle, which states:

3-dimensional case: Suppose two regions in three-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross-sections of equal area, then the two regions have equal volumes.
(Wikipedia)

So basically if we take a planar/horizontal cross section of the two napkin rings we are trying to compare, since they both have the same height, then this would allow us to compare their total volumes through comparing their respective areas at the cross section.

A planar horizontal cross section through 2 different sizes spheres. Areas to be compared shown in blue

So, based on Pythagorean theorem, we already know that the radius of a cylinder is calculated according to :

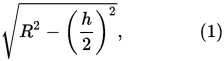
With R being the radius of the Sphere, and h the length of the napkin ring.
And then the radius of that cross section we did:

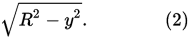
where y is actually the height between the equator of the sphere, and the location of that cross-section.

Now to calculate the area of that cross-section of the napkin ring, we would need to calculate the difference between the area of the large circle (using π * Radius ²) minus the area of the smaller circle (again π * radius ²), as follows:

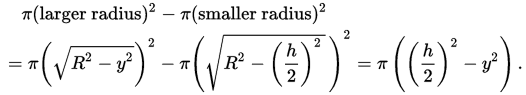
Whereby as you clearly notice, the radius (R) of the cylinder has been cancelled out of the equation (πR² - πR²), and hence the Radius of the cylinder is irrelevant.
And since h is equal across both napkin rings due to having same height, but also y being equal, as it represents the height at which the horizontal took place from the equator of each sphere, which basically means that they have same areas and hence same volume.

The Juice

So essentially, we just went through a proof confirming that the Radius of the originating sphere is irrelevant to the calculation of the volume, and hence, any two napkin rings with equal heights will have equal volumes according to Cavalieri's Principle.

So now next time you go to a wedding, or maybe at your own wedding, just keep in mind, you don't need bigger napkin rings to impress, eventually, they all have the same volume :)

Hope you found this entertaining and a cool learning experience!

@mcfarhat

---

References:

1. Wikipedia - Napkin Ring Problem
2. The Napkin Ring Problem - Youtube
3. Wikipedia - Napkin Rings
4. Wikipedia

Photo Credits:

1. Image 1
2. Image 2
3. Image 3
4. Image 4
5. Images 5, 6, 7

---

Founder of Arab Steem
Arab Steem is a community project to expand Steemit to the Arab world, by supporting the existing Arab steemians and promoting others to join.
You can connect with us on @arabsteem or via discord channel https://discord.gg/g98z2Ya
Your support is well appreciated!

---

Proud Member Of

• steemSTEM: SteemSTEM is a project that aims to increase both the quality as well as visibility of Science, Technology, Engineering and Mathematics (and Health). You can check out some great scientific articles via visiting the project tag #steemSTEM , project page @steemstem, or connecting with us on chat https://steemit.chat/channel/steemSTEM
• MAP(Minnows Accelerator Project): MAP is a growing community helping talented minnows accelerate their growth on Steemit.
  To join, check out the link at the home page of @accelerator account

---

Check our some of my Prior Posts

• Woo Product Remover - Clean up your online woocommerce installation
• Century Old Mystery of The Zipf's Law (And A Cool Experiment)
• Day 7 of my #sevendaybnwchallenge photography
• Day 6 of my #sevendaybnwchallenge photography
• Auriez-Vous Avaler Une Batterie?
• Day 5 of my #sevendaybnwchallenge photography
• Since Bigger is Better: Meet UY Scuti
• Day 4 of my #sevendaybnwchallenge photography
• MRI Scans and How They Work
• Day 3 of my #sevendaybnwchallenge photography