How Many Balls Are In The Vase At Noon? (or The Ross-Littlewood Paradox)

So if you enjoyed our latest infinity related paradox post - Hilbert's Grand Hotel Paradox, today we got an even wayyyy cooler infinity related paradox, which i believe to be one of the most mind-blowing ones i've recently written about, and it's called:

The Ross-Littlewood Paradox
You can see an additional list of my other cool paradox posts at the end of the article, don't scroll down yet :D

---

What are we talking about?

So, the paradox essentially aims at answering the question of the post's title, "how many balls are in the vase at noon?"
You might think, tell me how big it is, i'll just calculate the volume, divide by the volume of each ball, and there you have it - mathematically speaking.
Well, there is a slight problem, actually few slight problems, since the paradox goes as follows:

---

Assumptions

• We have a giant vase, which is infinitely big, that can hold an infinite amount of balls.
• We also have an infinite amount of balls that we can insert into the vase.
• The balls are numbered in order 1, 2, 3, ...
• We are adding balls at a rate of 10 balls per each task.

Our imaginary vase and balls

• Tasks are performed at decreasing timing, with first task starting at 11:59:00 AM:
  The first task would is completed in half a min (1/2 min).
  The second task, would be completed in half the amount, so a quarter of a min (1/4 min).
  The third one, in half the last one's amount, so one eigth of a min (1/8 min).
  and so on and so forth...until, the last task to be completed by noon.

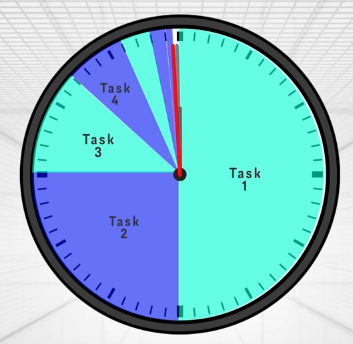
Time lapse of the different tasks

So basically, it drills down to performing an infinite amount of tasks, in an finite amount of time, which is the definition of what we refer as a supertask.

---

Cool Fact: If we stay in the realm of possible, supertasks simply cannot exist, due to both space and time's properties of NOT being infinitely divisible.
In the real world, or at least the known universe, the smallest distance is actually the Planck length = 1.616 299(38)x10^-35meters, which practically translates to 100 quintillionth of proton's diameter.
Similarly, the Planck time, is the fastest time to travel through the Planck length at the speed of light, which is equal to 5.391 16(13)x10^-44seconds
Yet, Math simply doesn't care about limitations, nor does the human mind, so on with our quest :)

Now, let us consider several scenarios of how we are feeding the balls into the vase, and then get an answer to our question, how many balls are in the vase at noon..

---

Scenario one: Adding 10 balls and removing the first

10 balls to be added at each task

So in this scenario, we start with task 1, where we add balls 1 to 10, and remove the first, which is ball 1
At task 2, we add balls 11-20, and remove the remaining first, which is ball 2
At task 3, we add balls 21-30, and remove the remaining first, ball 3,
And so on and so forth...

Balls in the vase after 3 tasks

Now the question is .. how many balls would be in the vase at noon?
My personal guess was, well, as probably many of you would suggest, infinity.
And that is actually INCORRECT

But how, we just practically added 9, and then another 9, and yet another 9,... so we should have .. infinity?

Let us look into what happened on the actual the steps. At step 1, we removed ball 1, and then step 2, removed ball 2, step 3, removed ball 3,...so at step n, we would remove ball n, and hence all the balls will be removed from the vase by the end of the tasks

Progress of removing balls at every step

But wait, there's more...

Apparently, the order in which we add balls, and remove them, affects how many balls are in the vase at noon. Let us look at an alternative scenario..

---

Scenario two: Adding 10 balls and removing the last

So in this alternative scenario, let us proceed as follows:
At task 1, we add balls 1 to 10, and remove the last, which is ball 10
At task 2, we add balls 11-20, remove the last, which is ball 20
At task 3, we add balls 21-30, remove the last, ball 30,
And so on and so forth...

Balls in vase at end of task 4

So again, how many balls would be in the vase at noon?
This time, the answer is different, and it is Infinity.

Seriously? yes seriously.

This is actually due to the fact that only balls which are multiples of ten are the ones being removed, so the vase will not contain balls 10, 20, 30,... yet all the other balls will still be there, hence the infinite amount.

---

Other answers?

Other philosophers had different opinions about this problem statement.
For instance, philosopher mathematician Paul Benacerraf claimed that the problem statement is not well specified, since it explains all the steps that happen prior to reaching noon, yet no specification is clear about noon. The vase might as well burst into dust, blow up...
Another philosopher, Jean Paul Van Bendegem, claimed that the problem is not properly formed, due to the fact that noon is a moment that can never be reached because of the infinite amount of tasks that need to be done. And the question in itself is assuming that noon will be reached, which is contradictory.

---

Not to forget proper historical acknowledgment

The Ross-Littlewood paradox was actually initially formulated in 1953 by mathematician John E. Littlewood, and then expanded in 1988 by Sheldon Ross.

---

What to take from this?

So at the end, while this might seem like a crazy concept to dwel upon, or something that would never happen in our universe, yet it is such a challenging thought, such an out of the box thinking that grows our knowledge, helps us explore uncharted territories, and that made us who we are at the moment.

Hope you found this as fun and educational as I did !

@mcfarhat

Other cool paradoxes i've recently written about:

• Hilbert's Grand Hotel Paradox
• The Napkin Ring Paradox
• The Zipf's Law_

---

References:

• Wikipedia
• Wikipedia
• Youtube PBS Infinite Series
• Youtube Vsauce

Photo Credits:

• Images 1, 2, 3, 4, 5, 6

---

Founder of Arab Steem
Arab Steem is a community project to expand Steemit to the Arab world, by supporting the existing Arab steemians and promoting others to join.
You can connect with us on @arabsteem or via discord channel https://discord.gg/g98z2Ya
Your support is well appreciated!

---

Proud Member Of

• steemSTEM: SteemSTEM is a project that aims to increase both the quality as well as visibility of Science, Technology, Engineering and Mathematics (and Health). You can check out some great scientific articles via visiting the project tag #steemSTEM , project page @steemstem, or connecting with us on chat https://steemit.chat/channel/steemSTEM
• MAP(Minnows Accelerator Project): MAP is a growing community helping talented minnows accelerate their growth on Steemit.
  To join, check out the link at the home page of @accelerator account