Magnetism: Part 8 - Paramagnetism

Previous posts: I, II, III, IV, V, VI, VII

 Welcome back, folks. In the last post, we thought about the role of electron spin in the context of an isolated atom. We began our heuristic argument by considering the (Zeeman) energy due to a spin state that parallel to the z axis, in a magnetic field (see post V for an explanation of why this arises). We identified that as well as spin angular momentum, an atom also has orbital angular momentum, which we wrote down in maths as a sum over the oribal angular momentum states of the Z electrons associated with the atom. This enabled us to write the Hamiltonian in the absence of a magnetic field, which we called the unperturbed Hamiltonian. 

We then 'turned on' a magnetic field, and exploited the local gauge invariance of the magnetic vector potential, so that we could rewrite the kinetic energy using the canonical momentum relation (see post III), and uncover the perturbed Hamilonian. From this simple argument, we were able to identify a different type of magnetism, known as paramagnetism, which this post will consider in more detail. 

---

Image credit/source. 

---

Paramagnetism: Introduction

In contrast to diamagnetism, paramagnetism corresponds to a positive susceptibility. This means that an applied magnetic field induces a net magnetisation within the paramagnetic sample, which aligns parallel with the applied magnetic field which brought it about. In our previous treatments, we considered atoms which have no unpaired electrons, hence no net magnetic moment. We are now concerned with atoms that do have unpaired electrons, and as a result have non-zero magnetic moment, even in the absence of an applied field. In general, paramagnetic effects are much stronger than diamagnetic effects, although diamagnetism is always present in any given material. 

In a paramagnetic sample at zero applied field, all the magnetic moments point in random directions because the magnetic moments on neighbouring atoms interact only very weakly with eachother. We treat the magnetic moments as being independent of one another. Now, when a magnetic field is applied, all the moments align with one another, with the global alignment of spins within a sample quantified via the magnetisation, which depends on the strength of the applied magnetic field (more field; more alignment - simple). 

The magnetic moment on an atom is associated with its total angular momentum J which is a sum of the orbital angular momentum L and the spin angular momentum S, so that 

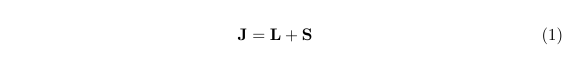
From this point forth in the series for the sake of convinience, we will use the following 'God given units',

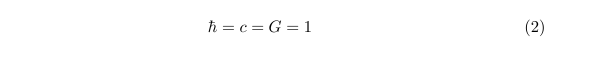
It's important to remember, therefore, that we are now considering J, L and S in units of h/2pi (i.e. hbar). One final word, before we consider paramagnetism semiclassically: if we increase the magnetic field, we expect the magnetisation to increase, however, if we increase the temperature, we would expect the resulting phonon scattering processes to randomise the orientation of the magnetic moments. We therefore expect that the magnetisation of a paramagnetic sample is dependent upon the ratio B/T. 

Semiclassical treatment of paramagnetism

In this treatment of paramagnetism, we ignore the fact that magnetic moments can point only along certain directions due to quantisation, and consider the magnetic moments lying at an angle between theta and theta + d(theta) to the applied magnetic field, B, which we assume to be along the z direction. These magnetic moments, therefore have an energy of - mu B cos(theta), and have a net magnetic moment along B equal to + mu cos(theta). 

If the magnetic moments could choose any direction to point along at random, the fraction which would have an angle between theta and theta + d(theta) would be proportional to the area of an annulus of the unit sphere (radius = 1). By calculating the total surface area of the sphere we are able to determine this fraction. The probability of having an angle in this interval is simply propoertional to the product of this statistical factor and the Boltzmann factor. The average moment along B is then

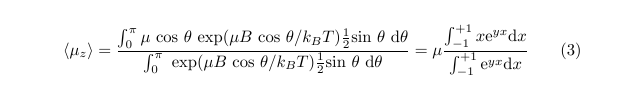
where we have defined y = mu B / kT, and x = cos(theta). This leads to 

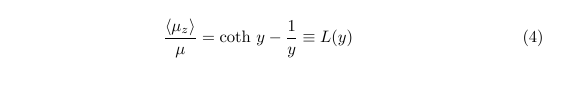
where L(y) is the so-called Langevin function. If we denote the number of magnetic moments per unit volume as n, then we can write the saturation magnetisation (the maximum magnetisation we can obtain when all moments are aligned), so that M_s = n mu.  By considering the ratio between the magnetisation we have derived, and the saturation magnetism, we recover the useful relationship for the paramagnetic susceptibility (in the weak field limit) as:

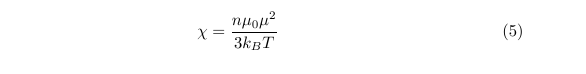
which shows us that the magnetic susceptibility is inversely proportional to the temperature, which is known as Curie's law, after Pierre Curie who discovered the temperature dependence of paramagnetism. 

---

References & Further Reading:

• Magnetism in Condensed Matter, Stephen Blundell, Oxford University Press, New York, 2003.
• Physics of Magnetism,  Sōshin Chikazumi,  Wiley, 1964.

---

Thanks for reading. In the next post, our mission will be to generalise our current treatment of paramagnetism, before moving beyond a semiclassical treatment towards a fully quantised description.