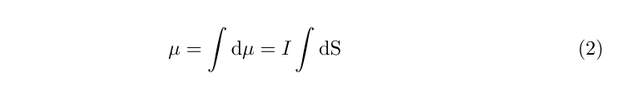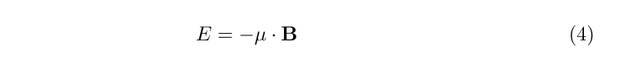Magnetism: Part 1 - Introduction
Hey folks, over the course of this series of posts, we will try to gain an understanding of some of the key concepts in magnetism. Some of this treatise will be mathematical, but I'm hoping I can convey the underlying ideas in an accessible manner. In this first installment, we will get some of the basics sorted.
Magnetic moments
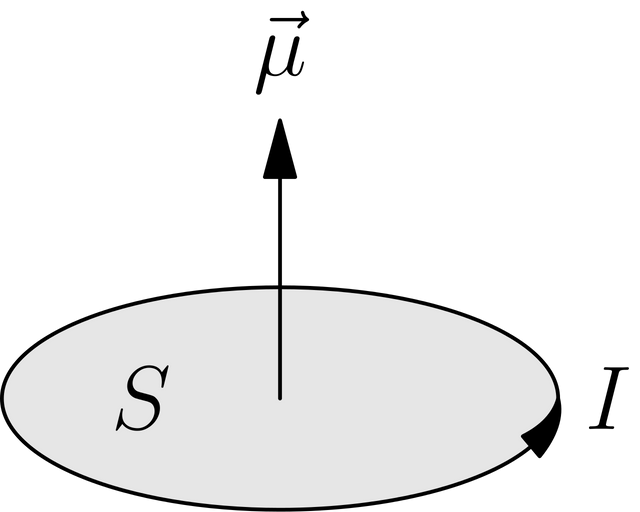
These are the fundamental 'objects' in magnetism. Imagine, for a moment, within the regime of classical electromangetism, that we have a current loop. Now, if this loop is vanishingly small, with an area |dS|, then the magnetic moment, d(mu) is given by
which has units of A m^2. The length of the vector dS is equal to the area of the loop, and the direction of the vector is normal to the loop.
The object we have just desribed is equivalent to a magnetic dipole, owing its name to an electric dipole due to their close comparability. We can picture, in our minds an object for which two mangetic molopoles, opposite in magnetic charge are separated by a small distance, which is parallel to the dS vector.
Associated with the charge going around the loop is an angular momentum vector, which, since the magnetic moment points normal to the plane of the loop of current, the magnetic moment can be parallel or antiparallel to the angular momentum vector.
We can calculate the magnetic moment mu of a finite sized loop by adding up the infinitesimal fragments that constitue the loop. All the currents from the neighbouring loops within the main loop cancel, ealving only a current around the perimeter of the loop, leading us to
Magnetic moments and angular momemtum
A current loop comes about as a result of the motion of one or more electrical charges. We are only going to consider particles in this treatise that have mass, therefore we also have to deal with orbital motion of mass alongside that of charge in the current loop.
In atoms, in particular, the magnetic moment associated with an orbiting electron lies along the same direction as the angular momentum of the electron, L. It is also the case that the magnetic moment is proportional to L, therefore we can write
where gamma is a constant termed, the gryomagnetic ration. This relationship between the magnetic moment and the angular momentum is demonstrated by the Einstein-de Haas effect, in which a ferromangetic rod is suspended vertically, along its axis, by a thin fibre. It is initially at rest and unmagnetised, and is subsequently magnetised along its length by the application of an external, vertical magnetic field. This vertical magnetisation is due to the alignment of the atomic mangetic moments and corresponds to the net angular momentum. Now, in order to conserve angular momentum, the rod begins turning around its axis in the opposite sense.
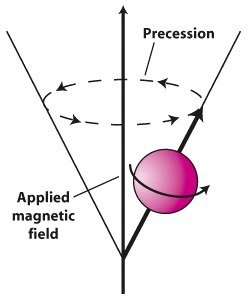
Precession
We now turn our attention to the situation in which we have a magnetic moment, mu in the vicinity of a magnetic field B. The energy of the magnetic moment is given by
so that the energy is a minimum when the magnetic moment is parallel to the applied field. There will be a torque G on the magnetic moment, which is given by
Now, since the magnetic field is associated with the angular momentum, L, and since the torque is equal to the rate of change of angular momentum, we can rewrite eq.(5) as
So rather than the magnetic moment leaning towards B, the magnetic field causes the direction of the magnetic moment to precess around B.