Magnetism: Part 2 - Introduction
Afternoon folks, in the last post, we understood the concept of a magnetic moment as an elementary object in magnetism, analogous to an electric dipole, and we considered the relationship between angular momentum and magnetic moments, which led us to the notion of precession. In this installment, we will introduce the Bohr magneton, and try to make some sense of magnetisation and field.

The Bohr magneton
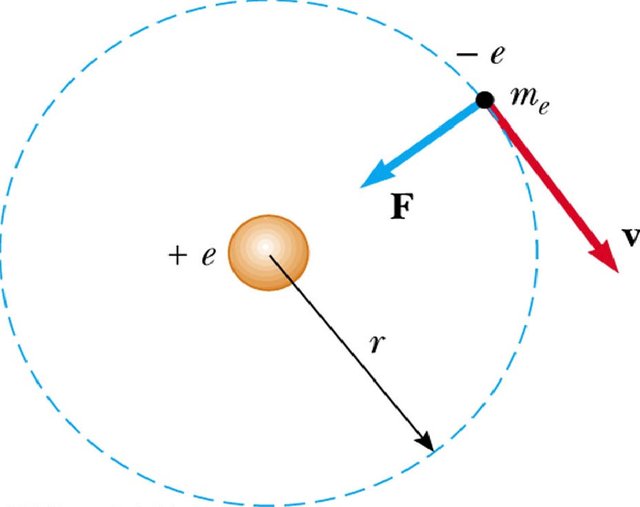
We can quite easily estimate the size of an atomic magnetic moment, and from this, we can deduce the size of the gyromagnetic ratio. As shown in the diagram below, imagine an electron (which has charge -e, and mass m_e) that is circularly orbiting the nucleus of a hydrogen atom. The current around the atom is
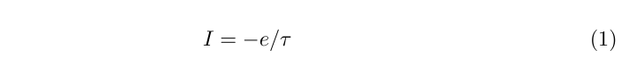
where the orbital period, tau, is given by

v = |v| is the speed, and r is the radius or the orbit. The magnitude of the angular momentum of the electron is given by mvr, and since angular momentum is quantised, it is the case that in the ground state, this quantity must be equal to h/2pi (hbar). We may, therefore, write the magnetic moment as
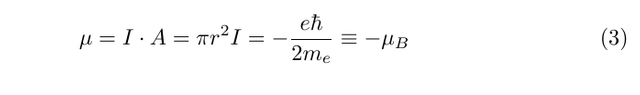
where mu_B is the Bohr magneton. This is a unit that is quite useful when describing the sizes of atomic moments, and takes the value 9.274 x 10^-24 Am^2. The gyromagnetic ratio for the electron is

and the Lamor precession frequency is then given by
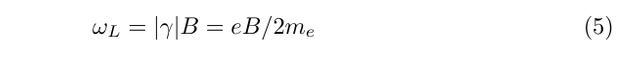
Magnetisation and field
In a magnetic solid, there are a huge number of atoms, each carrying a magnetic moment. The magnetisation, M is defined as the magnetic moment per unit volume. If we impose a continuum approximation, which smooths out the graininess which is present due to the individual atomic moments, then M can be considered to be a smooth vector field, which is continous at all points of its domain except at the edges of the magnetic solid. There is no magnetisation in free space (vacuum).
Now, in a vacuum, the magnetic field can be described via the vector fields B and H, which are related by

where mu_0 = 4pi x 10^-7 Hm^-1 is the permeability of free space. B is measured in tesla (T) and H is measured in Am^-1, and these two vector fields are just scaled versions of one another. The standard convention is that B is called the magnetic induction or magnetic flux density, and H is called the magnetic field strength.
The situation is slightly more complicated in a magnetic solid, with the relation between B and H given by
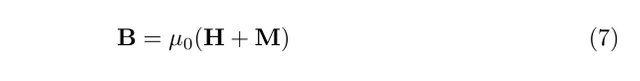
In the special case, whereby the magnetisation is linearly related to the magnetic field via a dimensionless quantity, chi, called the magnetic susceptibility, we may write

In this special case, we still have a linear relationship between B and H, given by
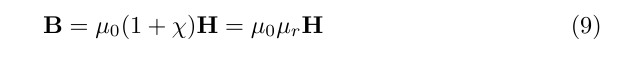
where mu_r = (1 + chi) is the relative permeability of the material.
In the next post, we will explore the effect of an applied magnetic field on a system of charges using classical mechanics, and the notion of canonical momentum.