Magnetism: Part 4 - Bohr-van Leeuwen theorem
In the last post, we introduced the magnetic vector potential and put it to good use in rewriting the Lorentz force for our charged particle moving in a magnetic and electric field, which led us to the definition of the canonical momentum. Ultimately, we are trying to describe the effect of an applied magnetic field on a system of charges, so given that we have determined the variation in momentum of a single charged particle, we will try to calculate the net magnetic moment of a system of electrons in a solid.

The Bohr-van Leeuwen theorem
We need to determine the magnetisation - the magnetic moment per unit volume, that is induced by a magnetic field. We have seen previously, that the magnetisation is proportional to the rate of change of energy of the system with applied magnetic field. Also, we saw in the last post, that the effect of a magnetic field is always to produce forces on charged particles which are perpendicular to their velocities. As a result of this fact, no work is done, and the energy of the system cannot depend on the applied magnetic field. So, if the energy of the system is not dependent upon the applied magnetic field, then there can be no magnetisation.
The Bohr-van Leeuwen theorem states:
In a classical system, there is no thermal equilibrium magnetisation.
Proof
The partition function Z, for N particles, each with charge q, can be written as
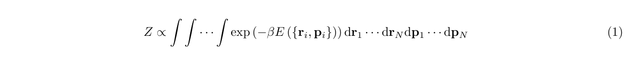
where beta = 1/kT, and i = 1,..., N. In this expression, the E term is the energy associated with the N charged particles under consideration, having positions r1, r2,...,rN, and momenta, p1, p2,...,pN. Our integral is thus over a 6N-dimensional phase space.
We saw previously, that the effect of a magnetic field is to shift the momentum of each particle by the quantity qA, therefore we replace pi by (pi - qA). This shift in the momentum is absorbed by the limits of integration, which range from -infinity to +infinity, by shifting the origin of the momentum integrations.
As a result of this, we see that the partition function, Z, is not a function of magnetic field, nor is the free energy, which is given by
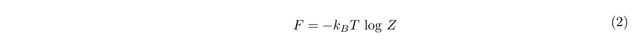
This leads us directly to the statement that magnetisation must be zero in a classical system, proving the Bohr-van Leeuwen theorem. For a rigorous proof in the semi-classical limit, see this excellent paper.
Discussion
When there is no applied magnetic field, electrons travel along straight paths, and when an external magnetic field is applied, they follow helical paths, and perform cyclotron orbits. Now, electrons do perform these orbits in materials, however the electrons near the surface cannot perform complete loops, but instead perform skipping-orbits around the perimiter. The anticlockwise current which comes about due to the bulk electrons cancels exactly the clockwise current generated by the skipping orbits of electrons that reflect or scatter at the surface of the material.
But, something is quite obviously is wrong, and I hope you have realised by now! Some materials, that we see in everyday life do indeed have a net magnetisation, so what is going on here? We can only conclude that the assumptions made by the Bohr-van Leeuwen theorem are not sufficient to describe the magnetisation of materials. What was assumed? Classical mechanics. In order to explain the magnetisation of a material, we must approach the problem via quantum theory.